呼和浩特专版2020中考数学复习方案第七单元图形的变化第31课时视图投影与尺规作图课件 45页

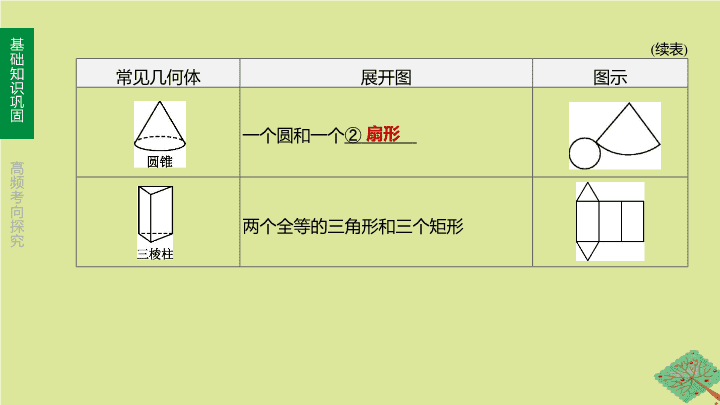
第 31 课时　 视图、投影与尺规作图 第七单元　图形的变化 常见几何体 展开图 图示 六个全等的正方形 两个同等大小的圆和一个 ① 　　　   考点一　立体图形的展开与折叠 考点聚焦 矩形 1 . 常见几何体的展开图 ( 续表 ) 常见几何体 展开图 图示 一个圆和一个 ② 　　　   两个全等的三角形和三个矩形 扇形 2 . 正方体表面展开图类型 ( 相同颜色表示相对的面 ) 一四一型 二三一型 二二二 型 三三型 【 记忆口诀 】 中间四个面 , 上下各一面 ; 中间三个面 , 一二隔河见 ; 中间两个面 , 楼梯天天见 ; 中间没有面 , 三三连一线 . 【 温馨提示 】 (1) 正方体表面展开图中不能出现 图形 ; (2) 若出现 类型 , 另外两面必定在两侧 , 可借助此特点来排除错误选项 . 考点二　投影的基本概念 平行投影 　 由 ③ 　　　　 光线形成的投影叫做平行投影 ; 物体在太阳光照射下可以看成平行投影 ; 投影线 ④ 　　　　 于投影面产生的投影叫做正投影   中心投影 　 由同一点 ( 点光源 ) 发出的光线形成的投影叫做中心投影 , 如灯光下某物体的投影 平行 垂直 考点三　三视图 1 . 三视图的概念及画法 三 视 图 主视图 　 正投影情况下 , 在正面内得到的 ⑤ 　　 　 观察物体的视图   左视图 　 正投影情况下 , 在侧面内得到的 ⑥ 　　　 观察 物体的视图   俯视图 　 正投影情况下 , 在水平面内得到的 ⑦ 　　 　 观察 物体的视图   画 法 主视图 和俯视图要 ⑧ 　　 　 ,  主视图和左视图要 ⑨ 　　　 ,   左视图和俯视图要 ⑩ 　　　　 ,   看得见的轮廓线通常画成 ⑪ 　　　　 ,  看不见的轮廓线通常画成 ⑫ 　　　   从前向后 从左到右 从上到下 长对正 高平齐 宽相等 实线 虚线 2 . 常见几何体的三视图 几 何 体 三 视 图 3. 根据三视图还原几何体 图 31-1 考点四　五种基本尺规作图 　　 定义 类型 　　 　 用无刻度的直尺和圆规作图叫尺规作图 1 . 作一条线段等于已知线段 步骤 : (1) 作射线 OP ; (2) 在 OP 上截取 ⑬ 　 　 ,  OA 即为所求线段 OA=a ( 续表 ) 　　 定义 类型 　　 　 用无刻度的直尺和圆规作图叫尺规作图 2 . 作一个角等于已知角 步骤 : (1) 作射线 O'A ; (2) 在 ∠ α 上以 O 为圆心 , 以任意长为半径作弧 , 交 ∠ α 的两边于点 P , Q ; (3) 以 O' 为圆心 , OP 长为半径作弧 , 交 O'A 于点 M ; (4) 以点 M 为圆心 , 以 ⑭ 　 　 　 为半径作弧 , 交前弧于点 N ;  (5) 过点 N 作射线 O'B , ∠ BO'A 即为所求角 PQ 的长 ( 续表 ) 　　 定义 类型 　　 　 用无刻度的直尺和圆规作图叫尺规作图 3 . 作一个角的平分线 步骤 : (1) 以点 O 为圆心 , 任意长为半径作弧 , 分别交 OA , OB 于点 N , M ; (2) 分别以点 M , N 为圆心 , ⑮ 　　　　　 长为半径作弧 , 两弧在 ∠ AOB 内相交于点 P ;  (3) 作射线 OP , OP 即为所求 ( 续表 ) 　　 定义 类型 　　 　 用无刻度的直尺和圆规作图叫尺规作图 4 . 作线段的垂直平分线 步骤 : (1) 分别以点 A , B 为圆心 , ⑯ 　　　　　 长为半径向线段两侧作弧 , 两弧分别交于点 M , N ;  (2) 过点 M , N 作直线 , 所得直线 MN 即为所求 ( 续表 ) 　　 定义 类型 　　 　 用无刻度的直尺和圆规作图叫尺规作图 5 . 过直线上一点作已知直线的垂线 步骤 : (1) 以点 O 为圆心 , 任意长为半径作弧 , 交直线于 A , B 两点 ; (2) 分别以点 A , B 为圆心 , 以 大于 AB 长为半径向直线上方作弧 , 交点为 M ; (3) 作直线 MO , MO 即为所求 题组一　必会题 对点演练 图 31-2 [ 答案 ] B 　 [ 解析 ] 在 △ ABC 中 , ∵∠ B= 30°, ∠ C= 90°, ∴∠ BAC= 180°- ∠ B - ∠ C= 60°, 由作图可知 MN 为 AB 的垂直平分线 , ∴ DA=DB , ∴∠ DAB= ∠ B= 30°, ∴∠ CAD= ∠ BAC - ∠ DAB= 30°, 故选 B . 2 . 图 31-3 中的三视图对应的几何体是 ( 　　 ) 图 31-4 图 31-3 C 3 . [ 七上 P123 习题 4 . 1 第 10 题 ] 如图 31-5 是一个小正方体的展开图 , 把展开图折叠成小正方体后 , 有 “ 建 ” 字一面的相对面上的字是 ( 　　 ) A . 和 B . 谐 C . 社 D . 会 图 31-5 [ 答案 ] D 　 [ 解析 ] 这是一个正方体的平面展开图 , 共有六个面 , 其中面 “ 建 ” 与面 “ 会 ” 相对 , 面 “ 设 ” 与面 “ 谐 ” 相对 , 面 “ 和 ” 与面 “ 社 ” 相对 . 4 . [ 九下 P109 复习题 29 第 1 题改编 ] 如图 31-6 所示的三视图对应的物体是 　　　　 ( 填序号 ) .  图 31-7 (3) 图 31-6 5 . [ 九下 P99 例 5 改编 ] 某工厂要加工一批密封罐 , 设计者给出了密封罐的三视图 ( 如图 31-8) . 按照三视图确定制作每个密封罐所需钢板的面积为 　　　 mm 2 ( 图中尺寸单位 :mm) .  图 31-8 题组二　易错题 【 失分点 】 未分清三视图中的实线与虚线、有圆心与不带圆心的区别 ; 由简单组合体的三视图想象几何体时注意图形特征 , 不理解作图原理 , 不能利用作图痕迹判断是哪种尺规作图 . 6 . 如图 31-9 所示的几何体的左视图是 ( 　　 ) 图 31-9 图 31-10 D 7 . 数学活动课上 , 四位同学围绕作图问题 :“ 如图 31-11, 已知直线 l 和 l 外一点 P , 用直尺和圆规作直线 PQ , 使 PQ ⊥ l 于点 Q. ” 分别作出了下列四个图形 , 其中作法错误的是 ( 　　 ) 图 31-11 图 31-12 A 考向一　三视图 例 1 [2019· 菏泽 ] 一个几何体的三视图如图 31-13 所示 , 则这个几何体的表面积是 ( 　　 ) A . 5 cm 2 B . 8 cm 2 C . 9 cm 2 D . 10 cm 2 图 31-13 [ 答案 ] D 　 [ 解析 ] 由题意知该几何体是长方体 , 长、宽、高分别为 1 cm 、 1 cm 、 2 cm, ∴其表面积为 : 2×(1×1+1×2+1×2) = 10(cm 2 ), 故选 D . | 考向精练 | 1 . [2019· 呼和浩特 7 题 ] 如图 31-14 是一个几何体的三视图 , 其中主视图与左视图完全一样 , 则这个几何体的表面积是 ( 　　 ) A . 80-2π B . 80+4π C . 80 D . 80+6π 图 31-14 [ 答案 ] B 　 [ 解析 ] 由三视图可知几何体为一个长方体中间挖去一个圆柱体 , 其中长方体的长 , 宽 , 高分别为 4,4,3; 中间空缺部分为一个直径为 2, 高为 3 的圆柱体 . 其中上下底面积均为正方形面积减去圆的面积 , 外侧面积为长方体的侧面积 , 内侧面积为圆柱体的侧面积 . ∴ S 表 =S 上底 + S 下底 + S 外侧 + S 内侧 = (4×4-π)+(4×4-π)+(4×4×3)+(2π×3) = 32-2π+48+6π = 80+4π, 故选 :B . 2 . [2018· 呼和浩特 2 题 ] 下面是几个一样的小正方体摆出的立体图形的三视图 , 由三视图可知小正方体的个数为 ( 　　 ) A . 6 个 B . 5 个 C . 4 个 D . 3 个 图 31-15 C 3 . [2016· 呼和浩特 8 题 ] 一个几何体的三视图如图 31-16 所示 , 则该几何体的表面积为 ( 　　 ) A . 4π B . 3π C . 2π+4 D . 3π+4 图 31-16 D 4 . [2015· 呼和浩特 9 题 ] 如图 31-17 是某几何体的三视图 , 根据图中所标的数据求得该几何体的体积为 ( 　　 ) A . 236π B . 136π C . 132π D . 120π 图 31-17 B 图 31-18 C 6 . [2019· 呼和浩特一模 ] 由 6 个大小相同的正方体搭成的几何体 , 被小颖拿掉 2 个后 , 得到如图 31-19 ①所示的几何体 , 图②是原几何体的三视图 . 请你判断小颖拿掉的两个正方体原来放在 ( 　　 ) A . 1 号的前后 B . 2 号的前后 C . 3 号的前后 D . 4 号的左右 图 31-19 B 7 . [2018· 呼和浩特 34 中月考 ] 如图 31-20, 一个水平放置的圆锥的主视图为底边长 2 cm, 腰长 3 cm 的等腰三角形 , 则该圆锥的表面积是 　　　　 .  图 31-20 4π cm 2 考向二　立体图形的展开与折叠 图 31-21 例 2 [2019· 山西 ] 某正方体的每个面上都有一个汉字 , 如图 31-21 是它的一种展开图 , 那么在原正方体中 , 与 “ 点 ” 字所在面相对的面上的汉字是 ( 　　 ) A . 青 B . 春 C . 梦 D . 想 B | 考向精练 | 图 31-23 1 . [2019· 南充 ] 如图 31-22 是一个几何体的表面展开图 , 这个几何体是图 31-23 中的 ( 　　 ) C 图 31-22 2 . [2019· 遂宁 ] 如图 31-24 为正方体的一种平面展开图 , 各面都标有数字 , 则标有数字 -2 的面与其对面上的数字之积是 ( 　　 ) A . -12 B . 0 C . -8 D . -10  图 31-24 [ 答案 ] A 　 [ 解析 ] 正方体折叠还原后 -2 的对面是 6, ∴ -2×6 = -12 . 3 . 如图 31-25 的正方体盒子的外表面上画有 3 条粗黑线 , 将这个正方体盒子的表面展开 ( 外表面朝上 ), 展开图可能是 ( 　　 ) 图 31-25 图 31-26 [ 答案 ] D 　 [ 解析 ] 制作 A,B,C,D 选项图 , 由实践操作可知符合示意图的只有 D 选项 , 故选 D . 4 . [2019· 河北一模 ] 在图 31-27 上剪去一个图形 , 剩下的图形可以折叠成一个长方体 , 则剪去的这个图形是 ( 　　 ) A . ① B . ② C . ③ D . ④ 图 31-27 A 考向三　尺规作图 图 31-28 [ 答案 ] C | 考向精练 | 图 31-29 [ 答案 ] A 　 [ 解析 ] 由作图方法知 , MN 是线段 AB 的垂直平分线 , ∴ AD=BD , ∴ △ BDC 的周长 =BD + DC + BC=AD + DC + BC= 5+3 = 8 . 故选 A . [ 答案 ] D 　 3 . [2019· 赤峰 ] 如图 31-30, 已知 : AC 是 ▱ ABCD 的对角线 . (1) 用直尺和圆规作出线段 AC 的垂直平分线 , 与 AD 相交于点 E , 连接 CE. ( 保留作图痕迹 , 不写作法 ); (2) 在 (1) 的条件下 , 若 AB= 3, BC= 5, 求 △ DCE 的周长 . 图 31-30 解 :(1) 如图 , 直线 l 为线段 AC 的垂直平分线 , CE 为所作 . 3 . [2019· 赤峰 ] 如图 31-30, 已知 : AC 是 ▱ ABCD 的对角线 . (2) 在 (1) 的条件下 , 若 AB= 3, BC= 5, 求 △ DCE 的周长 . 图 31-30 (2) ∵四边形 ABCD 为平行四边形 , ∴ AD=BC= 5, CD=AB= 3, ∵点 E 在线段 AC 的垂直平分线上 , ∴ EA=EC , ∴ △ DCE 的周长 =CE + DE + CD=EA + DE + CD=AD + CD= 5+3 = 8 .