哈尔滨市2012年初中毕业学年调研测试 9页

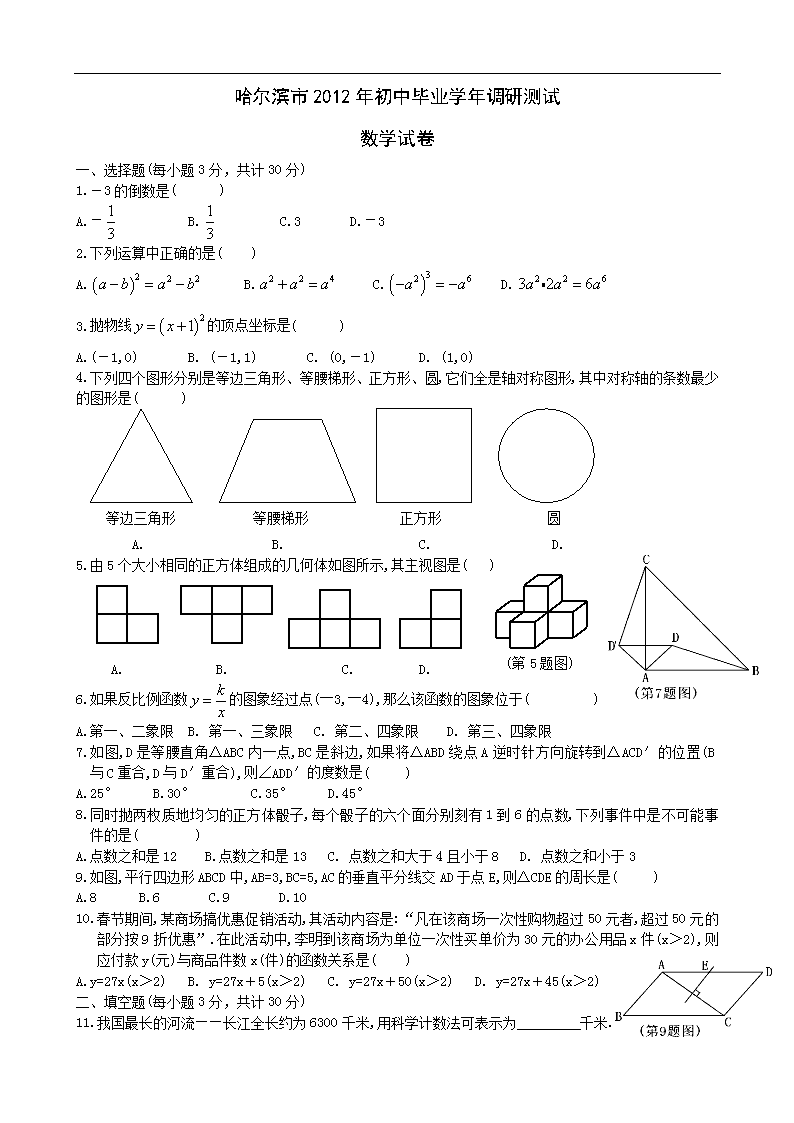
哈尔滨市2012年初中毕业学年调研测试 数学试卷 一、选择题(每小题3分，共计30分)‎ ‎1.－3的倒数是( )‎ A.－ B. C.3 D.－3‎ ‎2.下列运算中正确的是( )‎ A. B. C. D.‎ ‎3.抛物线的顶点坐标是( )‎ A.(－1,0) B. (－1,1) C. (0,－1) D. (1,0)‎ ‎4.下列四个图形分别是等边三角形、等腰梯形、正方形、圆,它们全是轴对称图形,其中对称轴的条数最少的图形是( )‎ 等边三角形 等腰梯形 正方形 圆 ‎ A. B. C. D.‎ ‎5.由5个大小相同的正方体组成的几何体如图所示,其主视图是( )‎ ‎(第5题图)‎ ‎ A. B. C. D.‎ ‎6.如果反比例函数的图象经过点(―3,―4),那么该函数的图象位于( )‎ A.第一、二象限 B. 第一、三象限 C. 第二、四象限 D. 第三、四象限 ‎7.如图,D是等腰直角△ABC内一点,BC是斜边,如果将△ABD绕点A逆时针方向旋转到△ACD′的位置(B与C重合,D与D′重合),则∠ADD′的度数是( )‎ A.25° B.30° C.35° D.45°‎ ‎8.同时抛两枚质地均匀的正方体骰子,每个骰子的六个面分别刻有1到6的点数,下列事件中是不可能事件的是( )‎ A.点数之和是12 B.点数之和是‎13 C. 点数之和大于4且小于8 D. 点数之和小于3‎ ‎9.如图,平行四边形ABCD中,AB=3,BC=5,AC的垂直平分线交AD于点E,则△CDE的周长是( )‎ A.8 B‎.6 C.9 D.10‎ ‎10.春节期间,某商场搞优惠促销活动,其活动内容是:“凡在该商场一次性购物超过50元者,超过50元的部分按9折优惠”.在此活动中,李明到该商场为单位一次性买单价为30元的办公用品x件(x＞2),则应付款y(元)与商品件数x(件)的函数关系是( )‎ A.y=27x(x＞2) B. y=27x＋5(x＞2) C. y=27x＋50(x＞2) D. y=27x＋45(x＞2)‎ 二、填空题(每小题3分，共计30分)‎ ‎11.我国最长的河流——长江全长约为6300千米,用科学计数法可表示为 千米.‎ ‎12.在函数y=中，自变量x的取值范围是 .‎ ‎13.不等式组的解集是 .‎ ‎14.把因式分解的结果是 .‎ ‎15.若圆锥的侧面展开图是一个弧长为36π的扇形,则这个圆锥底面的半径为 .‎ ‎16.如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则∠ACP的度数为 度.‎ ‎17.等腰三角形一腰上的高与腰长之比为1:2,则该等腰三角形顶角的度数为 度.‎ ‎18.如图,AB和AC分别是⊙O的直径和弦,OD⊥AC于D,连接BD、BC,AB=5,AC=4,则BD= .‎ ‎19.如图,D为AB的中点,将△ABC沿过D点的直线折叠,使点A落在BC边的点F处,若∠B=50°,则∠BDF=‎ ‎ 度.‎ ‎20.已知,如图,在△ABC中,AB=AC=10,延长AC到E,使CE=AC,边B点作BE的垂线交AC于D,若D为AC的中点,则BE的长为 .‎ 三、解答题(其中21-24题各6分，25、26题各8分，27、28题各10分，共60分)‎ ‎21.(本题6分)‎ 先化简，再求代数式的值，其中x=2tan45°－1.‎ ‎22. (本题6分)‎ 图1、图2分别是6×5的,网格,网格中每个小正方形的边长均为1,线段AB的端点在小正方形的顶点上,请在图1、图2中各画一个图形,分别满足以下要求:‎ ‎(1)在图1中画一个以线段AB为一边的菱形(非正方形),所画菱形各顶点必须在小正方形的顶点上.‎ ‎(2)在图2中画一个以线段AB为一边的等腰三角形,所画等腰三角形各顶点必须在小正方形的顶点上,且所画等腰三角形的面积为.‎ ‎23.(本题6分)‎ 如图,四边形ABCD的对角线AC和BD相交于点O,∠1=∠2,∠3=∠4,求证:BO=DO.‎ ‎23.(本题6分)‎ 为了美化环境,计划将一个边长为‎4米的菱形草地ABCD分割成如图所示的四块,其中四边形AEPM和四边形NPFC均为菱形,且∠A=120°,若AE的长为x米, 四边形BEPN和四边形DMPF的面积和为S平方米.‎ ‎(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围);‎ ‎(2)根据(1)中的函数关系式,计算当x为何值时S最大,并求出最大值.‎ ‎【参考公式：二次函数y=ax2+bx+c(a≠0)，当x=-时，y最大(小)值=】‎ ‎25.(本题8分)‎ 为了解某学校学生的个性特长发展情况,学校决定围绕“音乐、体育、美术、书法、其它活动项目中,你参加哪一项活动(每人只限一项)的问题”,在全校范围内随机抽取部分学生进行问卷调查，并将调查结果绘制成如图所示的条形统计图,请根据图中提供的信息解答下列问题：‎ ‎(1)在这次调查中一共抽查了多少名学生?‎ ‎(2)求参加“音乐”活动项目的人数占抽查总人数的百分比.‎ ‎(3)若全校有2400名学生，请估计该校参加“美术”活动项目的人数.‎ ‎26.(本题8分)‎ ‎ 甲、乙两人从A地前往B地,AB两地的路程为180千米,乙的速度是甲的速度的1.5倍,甲比乙早出发0.5小时,结果甲比乙晚到0.5小时.‎ ‎(1)求甲乙两人的速度分别是多少?‎ ‎(2)甲到达B地后与乙同时按原速度返回A地,若它们由B地返回A地的过程中所行走路程的和不少于150千米,则它们至少要行走多少小时?‎ ‎27.(本题10分)‎ 如图：在平面直角坐标系中，直线与x轴、y轴分别交于A、B两点,直线与直线AB相交于点D,与x轴相交于点C,过D作DE⊥x轴,E为垂足,E点的横坐标为2. ‎ ‎(1)求直线CD的解析式；‎ ‎(2)若点P为x轴上一点,P点的坐标为(t,0),过P作x轴的垂线,交直线AB于点Q,边Q点作x轴的平行线交直线CD于点M,设线段QM的长为y,当－6＜t＜2时,求y与t的函数关系式;‎ ‎(3)在(2)的条件下，当t为何值时,过P、Q、M三点的圆与直线AB和直线CD这两条直线只有三个公共点.‎ ‎28.(本题10分)‎ 已知: △ABC中,∠ACB=2∠ABC,AD为∠BAC的平分线,E为线段AC上一点,过E作AD的垂线交直线AB于F.‎ ‎(1)当E点与C点重合时(如图1)，求证：BF=DE；‎ ‎(2)连接BE交AD于点N,M是BF的中点,连接DM(如图2)，若DM⊥BF,DC=4,S△ABD:S△ACD=3:2,求DN的长.‎