2017年江西省中考数学试卷 19页

江西省 2017 年中等学校招生考试 数学试题卷 一、选择题（本大题共 6 个小题,每小题 3 分,共 18 分.在每小题给出的四个选项中，只有一 项是符合题目要求的.） 1.-6 的相反数是（ ） A． 1 6 B． 1 6  C． 6 D．-6 2. 在国家“一带一路”战略下，我国与欧洲开通了互利互惠的中欧班列.行程最长，途经城市和国家最多 的一趟专列全程长 13000 km ，将 13000 用科学记数法表示应为（ ） A． 50.13 10 B． 41.3 10 C． 51.3 10 D． 313 10 3.下列图形中，是轴对称图形的是（ ） A． B． C． D． 4. 下列运算正确的是（ ） A． 25 10a a  B． 2 22 3 6a a a C. 2 3a a a    D． 6 2 36 2 3a a a    5.已知一元二次方程 22 5 1 0x x   的两个根为 1 2,x x ，下列结论正确的是（ ） A． 1 2 5 2x x   B． 1 2 1x x  C. 1 2,x x 都是有理数 D． 1 2,x x 都是正数 6. 如图，任意四边形 ABCD 中， , , ,E F G H 分别是 , , ,AB BC CD DA 上的点，对于四边形 EFGH 的形状， 某班学生在一次数学活动课中，通过动手实践，探索出如下结论，其中错误的是（ ） A．当 , , ,E F G H 是各边中点，且 AC BD 时，四边形 EFGH 为菱形 B．当 , , ,E F G H 是各边中点，且 AC BD 时，四边形 EFGH 为矩形 C. 当 , , ,E F G H 不是各边中点时，四边形 EFGH 可以为平行四边形 D．当 , , ,E F G H 不是各边中点时，四边形 EFGH 不可能为菱形 二、填空题（本大题共 6 小题，每小题 3 分，满分 18 分，将答案填在答题纸上） 7. 函数 2y x  中，自变量 x 的取值范围是___________． 8. 如图 1 是一把园林剪刀，把它抽象为图 2，其中OA OB ，若剪刀张开的角为 30°，则 A  _________ 度． 9. 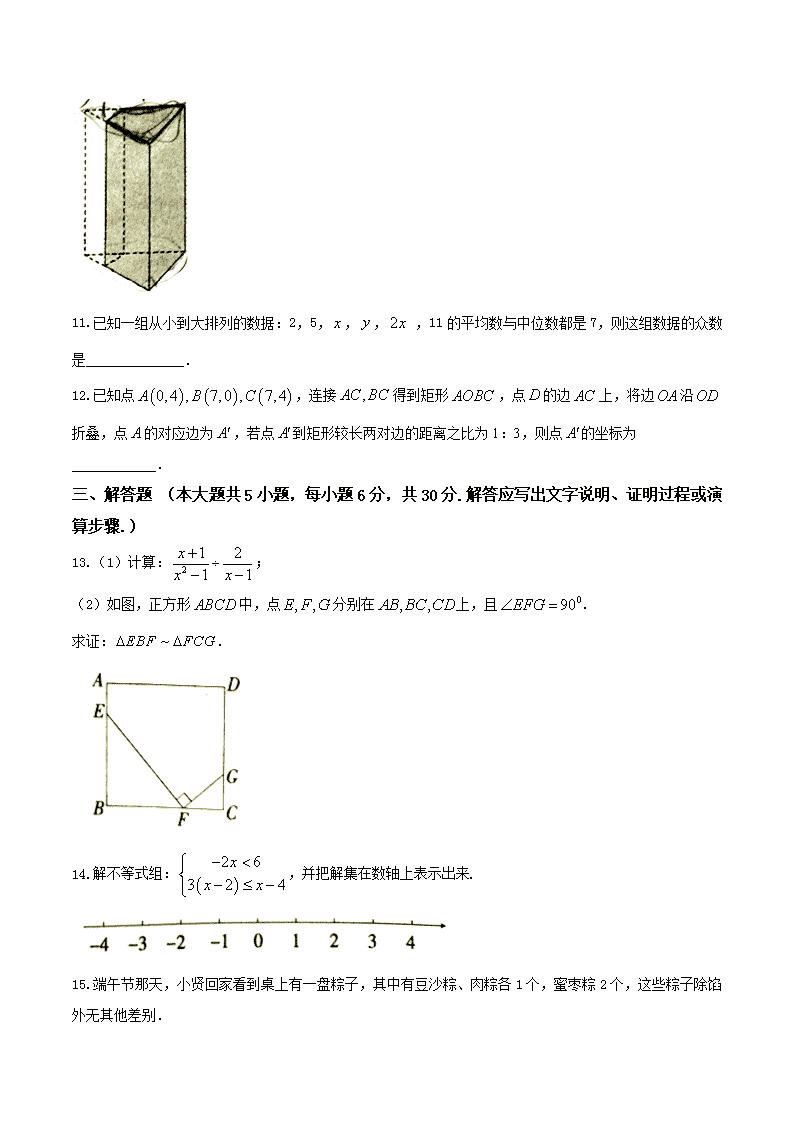中国人最先使用负数，魏晋时期的数学家刘徽在“正负术”的注文中指出，可将算筹（小棍形状的记数 工具）正放表示正数，斜放表示负数.如图，根据刘徽的这种表示法，观察图①，可推算图②中所得的数值 为___________． 10.如图，正三棱柱的底面周长为 9，截去一个底面周长为 3 的正三棱柱，所得几何体的俯视图的周长是 _____________． 11.已知一组从小到大排列的数据：2，5， x ， y ， 2x ，11 的平均数与中位数都是 7，则这组数据的众数 是______________． 12.已知点      0,4 , 7,0 , 7,4A B C ，连接 ,AC BC 得到矩形 AOBC ，点 D 的边 AC 上，将边OA 沿OD 折叠，点 A 的对应边为 A，若点 A到矩形较长两对边的距离之比为 1：3，则点 A的坐标为____________． 三、解答题 （本大题共 5 小题，每小题 6 分，共 30 分.解答应写出文字说明、证明过程或演 算步骤.） 13.（1）计算： 2 1 2 1 1 x x x    ； （2）如图，正方形 ABCD 中，点 , ,E F G 分别在 , ,AB BC CD 上，且 090EFG  . 求证： EBF FCG  . 14.解不等式组：   2 6 3 2 4 x x x       ，并把解集在数轴上表示出来. 15.端午节那天，小贤回家看到桌上有一盘粽子，其中有豆沙粽、肉粽各 1 个，蜜枣粽 2 个，这些粽子除馅 外无其他差别． （1）小贤随机地从盘中取出一个粽子，取出的是肉粽的概率是多少？ （2）小贤随机地从盘中取出两个粽子，试用画树状图或列表的方法表示所有可能的结果，并求出小贤取出 的两个都是蜜枣粽的概率. 16.如图，已知正七边形 ABCDEFG ，请仅用无刻度的直尺，分别按下列要求画图． （1）在图 1 中，画出一个以 AB 为边的平行四边形； （2）在图 2 中，画出一个以 AF 为边的菱形. 17. 如图 1，研究发现，科学使用电脑时，望向荧光屏幕画面的“视线角” 约为 20°，而当手指接触键 盘时，肘部形成的“手肘角” 约为 100°.图 2 是其侧面简化示意图，其中视线 AB 水平，且与屏幕 BC 垂 直. （1）若屏幕上下宽 20BC cm ，科学使用电脑时，求眼睛与屏幕的最短距离 AB 的长； （2）若肩膀到水平地面的距离 100DG cm ，上臂 30DE cm ，下臂 EF 水平放置在键盘上，其到地面 的距离 72FH cm .请判断此时  是否符合科学要求的 100°？ （参考数据： 0 0 0 014 14 4 14sin 69 ,cos21 ,tan 20 ,tan 4315 15 11 15     ，所有结果精确到个位） 四、（本大题共 3 小题，每小题 8 分，共 24 分）. 18. 为了解某市市民“绿色出行”方式的情况，某校数学兴趣小组以问卷调查的形式，随机调查了某市部 分出行市民的主要出行方式（参与问卷调查的市民都只从以下五个种类中选择一类），并将调查结果绘制成 如下不完整的统计图. 种类 A B C D E 出行方式 共享单车 步行 公交车 的士 私家车 根据以上信息，回答下列问题： （1）参与本次问卷调查的市民共有___________人，其中选择 B 类的人数有_____________人； （2）在扇形统计图中，求 A 类对应扇形圆心角 的度数，并补全条形统计图； （3）该市约有 12 万人出行，若将 , ,A B C 这三类出行方式均视为“绿色出行”方式，请估计该市“绿色出 行”方式的人数. 19.如图，是一种斜挎包，其挎带由双层部分、单层部分和调节扣构成.小敏用后发现，通过调节扣加长或 缩短单层部分的长度，可以使挎带的长度（单层部分与双层部分长度的和，其中调节扣所占的长度忽略不 计）加长或缩短.设单层部分的长度为 xcm ，双层部分的长度为 ycm ，经测量，得到如下数据： 单层部分的长度 x （ cm ） … 4 6 8 10 … 150 双层部分的长度  y cm … 73 72 71 … （1）根据表中数据的规律，完成以下表格，并直接写出 y 关于 x 的函数解析式； （2）根据小敏的身高和习惯，挎带的长度为120cm 时，背起来正合适，请求出此时单层部分的长度； （3）设挎带的长度为lcm ，求l 的取值范围. 20. 如图，直线  1 0y k x x  与双曲线  2 0ky xx   相交于点  2,4P .已知点    4,0 , 0,3A B ，连接 AB ，将 Rt AOB 沿OP 方向平移，使点O 移动到点 P ，得到 A PB  ．过点 A作 / /A C y 轴交双曲线于 点C . （1）求 1k 与 2k 的值； （2）求直线 PC 的表达式； （3）直接写出线段 AB 扫过的面积. 五、（本大题共 2 小题，每小题 9 分，共 18 分）. 21.如图 1， O 的直径 12,AB P 是弦 BC 上一动点（与点 ,B C 不重合）， 030ABC  ，过点 P 作 PD OP 交 O 于点 D . （1）如图 2，当 / /PD AB 时，求 PD 的长； （2）如图 3，当  DC AC 时，延长 AB 至点 E ，使 1 2BE AB ，连接 DE ． ①求证： DE 是 O 的切线； ②求 PC 的长． 22.已知抛物线  2 1 : 4 5 0C y ax ax a    ． （1）当 1a  时，求抛物线与 x 轴的交点坐标及对称轴； （2）①试说明无论 a 为何值，抛物线 1C 一定经过两个定点，并求出这两个定点的坐标； ②将抛物线 1C 沿这两个定点所在直线翻折，得到抛物线 2C ，直接写出 2C 的表达式； （3）若（2）中抛物线 2C 的顶点到 x 轴的距离为 2，求 a 的值. 六、（本大题共 12 分） 23. 我们定义：如图 1，在 ABC 看，把 AB 点 A 顺时针旋转  0 00 180   得到 AB ，把 AC 绕点 A 逆时针旋转  得到 AC，连接 B C .当 0180   时，我们称 A B C   是 ABC 的“旋补三角形”， AB C  边 B C 上的中线 AD 叫做 ABC 的“旋补中线”，点 A 叫做“旋补中心”. 特例感知： （1）在图 2，图 3 中， AB C  是 ABC 的“旋补三角形”， AD 是 ABC 的“旋补中心”. ①如图 2，当 ABC 为等边三角形时， AD 与 BC 的数量关系为 AD  _____________ BC ； ②如图 3，当 090 , 8BAC BC   时，则 AD 长为_________________. 猜想论证： （2）在图 1 中，当 ABC 为任意三角形时，猜想 AD 与 BC 的数量关系，并给予证明. 拓展应用 （3）如图 4，在四边形 ABCD ， 0 090 , 150 , 12C D BC     ， 2 3, 6CD DA  .在四边形内部是 否存在点 P ，使 PDC 是 PAB 的“旋补三角形”？若存在，给予证明，并求 PAB 的“旋补中线”长； 若不存在，说明理由. 参考答案 CBCADD 2x  75° -3 8 5 ( 7,3) 15 (2 3, 2)、（ ，1）或 13. 1 1= ( 1)( 1) 2 1 2 x x x x     解：原式 90° 90° 90° 90° = ABCD B C EFG EFB GFC EFB FEB FEB GFC EBF FCG                       证明： 正方形 ， 又 又 14. 3 2x  解： 15. 1 6 解： 16. 解答： 17. =tan20° 20 55tan20° (2) = cm 30 cm 28 14sin = = sin69°30 15 69° =180° 69°=111°>100° 100° BC AB AB cm FE DG DG P DE DPDEP DE DEP                 解：(1) 延长 至 交 于 则DP DG-FH=100-72=28 又 此时的 不符合科学要求的 18. 800 人，240 人， 090a  ， 25% 30% 25% =  （ ） 120000 96000（人） 19. 175 2 120 175 2 90 90cm30 75 1    50 y x x y y x x y l            解：（1） （2）依题意得： 解得： 此时单层部分的长度为 （3） 20. 21.   tan30° 2 60° 2 12 90° 30° 6 3, 3 3 3 3 3 3 3 =2 6 DC AC DOE OE OD ODE ODE DE DB AC DBP OBP BP BP DB OB DBP OBP BC B OP P PC r PD                                  ①证明：连接OD 又 是直角三角形， 解：（1）依题意得： 根据勾股定理可得 （ 且 是 O的切线 ② 连接 又 2） 、 ，可知 22. 2 2 2 2 2 2 2 4 5 ( 4 ) 5 0 4 5 4 4 5 4 5 4 5 ( 2) 4 5 4 5 2 4 5 2 7 3 4 4 y ax ax x ax a x y ax ax x y ax ax y ax ax y ax ax a x a a a a a                                   解：（1）点（-4,0），（5,0） （2） 当 时，函数 恒经过点（0，-5） 当 时，函数 恒经过点（4，-5） （ ① 3）依题意得： 或 式： 或 ②C 解析 23. 1 2 ，4， 解（2）猜想 1 2AD BC 解题过程：如图，将三角形 DAC 绕点 D 逆时针旋转，使 DC 与 DB 重合，证明 QB A CAB   0 090 , 150 , 12 2 3, 6 =2 39 2 39 = 39 C D BC CD DA BD AB BD AB P ABCD AB             解：存在. 连接BD,延长CD作BC的平行线交CD延长线于点E， ， 点 必在四边形 内 根据（3）所的结论：旋补中线等于 的一半可得 PF=