- 177.60 KB
- 2021-11-06 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
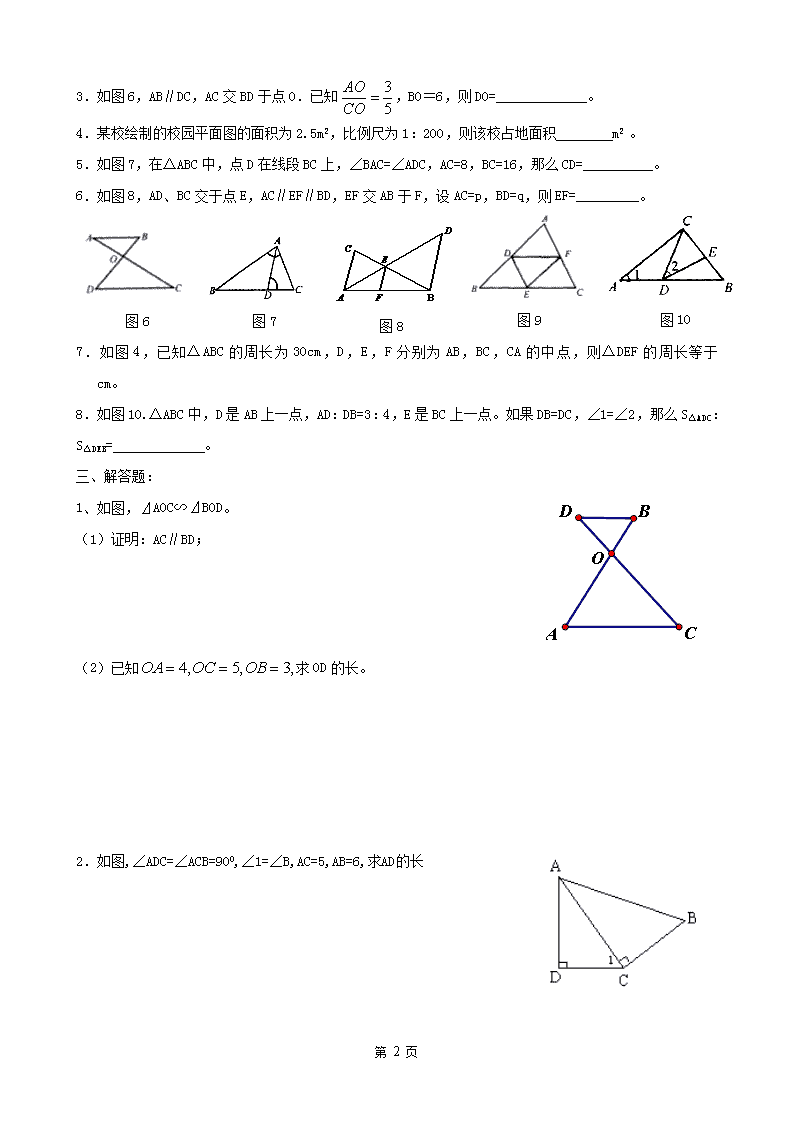
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
九年级上册数学相似三角形练习题
姓名: 日期:
一、选择题。
1.DE是DABC的中位线,则DADE与DABC面积的比是( )
A、 1:1 B、1:2 C、1:3 D、 1:4
2.如图1,已知△ADE∽△ABC,相似比为2:3,则=( )
A、3:2 B、2:3 C、 2:1 D、不能确定
3.如图2,已知△ACD∽△BCA,若CD=4,CB=9,则AC等于( )
A、 3 B、 4 C、 5 D、 6
4.△ADE∽△ABC,相似比为2:3,则△ADE与△ABC的面积比为( )
A、 2:3 B、 3:2 C、 9:4 D、 4:9
5.若DE是△ABC的中位线,△ABC的周长为6,则△ADE的周长为( )
A、4 B、3 C、2 D、1
6.如图3,△ABC中,DE∥BC,AD=1,DB=2,AE=2,那么EC=( )
图1
A、1 B、2 C、3 D、4
图5
图2
图3
图4
7.如图4,D是△ABC的AB边上的一点,过点D作DE∥BC交AC于E。已知AD:DB=2:3.则S△ADE:SBCED=( )
A、2:3 B、4:9 C、4:5 D、4:21
8. 如图5,已知:AD是Rt△ABC斜边BC上的高线,DE是RtCADC斜边AC上的高线,如果DC:AD=1:2,,那么 等于( )
A、 4a B、9a C、16a D、25a
二、填空题:
1.两个相似三角形的面积比为4∶25,则它们的周长比为 。
2.顺次连结三角形三边中点所构成的三角形与原三角形 ,它们的面积比为 。
第 5 页
3.如图6,AB∥DC,AC交BD于点O.已知,BO=6,则DO=_____________。
4.某校绘制的校园平面图的面积为2.5m2,比例尺为1:200,则该校占地面积 m2 。
5.如图7,在△ABC中,点D在线段BC上,∠BAC=∠ADC,AC=8,BC=16,那么CD=__________。
6.如图8,AD、BC交于点E,AC∥EF∥BD,EF交AB于F,设AC=p,BD=q,则EF=_________。
图10
图6
图8
图7
图9
图9
图8
图7
图6
7.如图4,已知△ABC的周长为30cm,D,E,F分别为AB,BC,CA的中点,则△DEF的周长等于 cm。
8.如图10.△ABC中,D是AB上一点,AD:DB=3:4,E是BC上一点。如果DB=DC,∠1=∠2,那么S△ADC:S△DEB= 。
三、解答题:
1、如图,⊿AOC∽⊿BOD。
(1)证明:AC∥BD;
(2)已知求OD的长。
2.如图,∠ADC=∠ACB=900, ∠1=∠B,AC=5,AB=6, 求AD的长
第 5 页
3.如图,在梯形ABCD中,AB⊥BC,∠BAD=90°,对角线BD⊥DC。
(1)△ABD与△DCB相似吗?请说明理由。 (2)如果AD=4,BC=9,求BD的长。
4.如图,矩形ABCD中,E为BC上一点,DF⊥AE于F.
(1)ΔABE与ΔADF相似吗?请说明理由.(2)若AB=6,AD=12,BE=8,求DF的长.
5.如图,已知是正方形的边上一点,于,求证:AB2=AE·BF。
6.已知:如图,△PMN是等边三角形,∠APB=120°。求证:AM·PB = PN·AP。
P
N
M
A
B
第 5 页
7.如图,△ABC中,D是AC的中点,E是BC延长线上一点,过A作AH∥BE,连结ED并延长交AB于F,交AH于H。(1)求证:AH=CE(2)如果AB=4AF,EH=8,求DF的长。
8.已知:如图:FGHI为矩形,AD⊥BC于D,,BC=36cm,AD=12cm 。求:矩形FGNI的周长。
9.如图,□ABCD中,E是CD的延长线上一点,BE与AD交于点F,。
⑴求证:△ABF∽△CEB;⑵若△DEF的面积为2,求□ABCD的面积。
10.如图,在ABCD中,过点B作BE⊥CD,垂足为E,连结AE,F为AE上一点,且∠BFE=∠C.(1)求证:△ABF∽△EAD;(2)若AB=4,∠BAE=30°,求AE的长;(3)在(1)(2)的条件下,若AD=3,求BF的长.
A
C
E
F
D
B
第 5 页
第 5 页
相关文档
- 2011年怀柔区初三数学一模试题答案2021-11-066页
- 2012年浙江省温州市初中毕业学业考2021-11-0613页
- 人教版九年级数学上册教案:23_3 课2021-11-063页
- 知识总结:初中化学常见的几种题型总2021-11-0610页
- 湖北省黄石市2020年初中毕业生学业2021-11-069页
- 2020九年级数学上册 第二十五章 概2021-11-065页
- 人教版九年级数学上册同步测试题(二2021-11-06230页
- 中考数学二轮精品练习:反比例函数2021-11-064页
- 2020九年级数学下册 第三章 圆2021-11-069页
- 江西省宜春黄冈实验学校2021届九年2021-11-069页