2021年中考数学专题复习 专题36 一次函数问题（学生版） 10页

专题 36 一次函数问题 一、一次函数 1．一次函数的定义 一般地，形如 y kx b  ( k ， b 是常数，且 0k  )的函数，叫做一次函数，其中 x 是自变量。 2．一次函数的图像：是不经过原点的一条直线。 3．一次函数的性质 (1)当 k>0 时，图象主要经过第一、三象限；此时，y 随 x 的增大而增大； (2)当 k<0 时，图象主要经过第二、四象限，此时，y 随 x 的增大而减小； (3)当 b>0 时，直线交 y轴于正半轴； (4)当 b<0 时，直线交 y轴于负半轴。 二、正比例函数 1．正比例函数的定义 一般地，形如 y=kx(k 是常数，k≠0)的函数叫做正比例函数，其中 k 叫做比例系数。正比例函数是一 次函数的特例，一次函数包括正比例函数． 2.正比例函数的图像：是经过原点的一条直线。 3．正比例函数的性质 (1)当 k>0 时，直线 y=kx 经过三、一象限，y 随 x 的增大而增大； (2)当 k<0 时，直线 y=kx 经过二、四象限，y随 x的增大而减小． 三、一次函数和正比例函数的关系 一次函数 y=kx＋b 的图象是一条直线，它可以看作是由直线 y=kx 平移|b|个单位长度而得到(当 b>0 时， 向上平移；当 b<0 时，向下平移) 四、用待定系数法确定函数解析式的一般步骤 (1)根据已知条件写出含有待定系数的函数关系式； (2)将 x、y 的几对值或图象上的几个点的坐标代入上述函数关系式中得到以待定系数为未知数的方程； (3)解方程得出未知系数的值； (4)将求出的待定系数代回所求的函数关系式中得出所求函数的解析式. 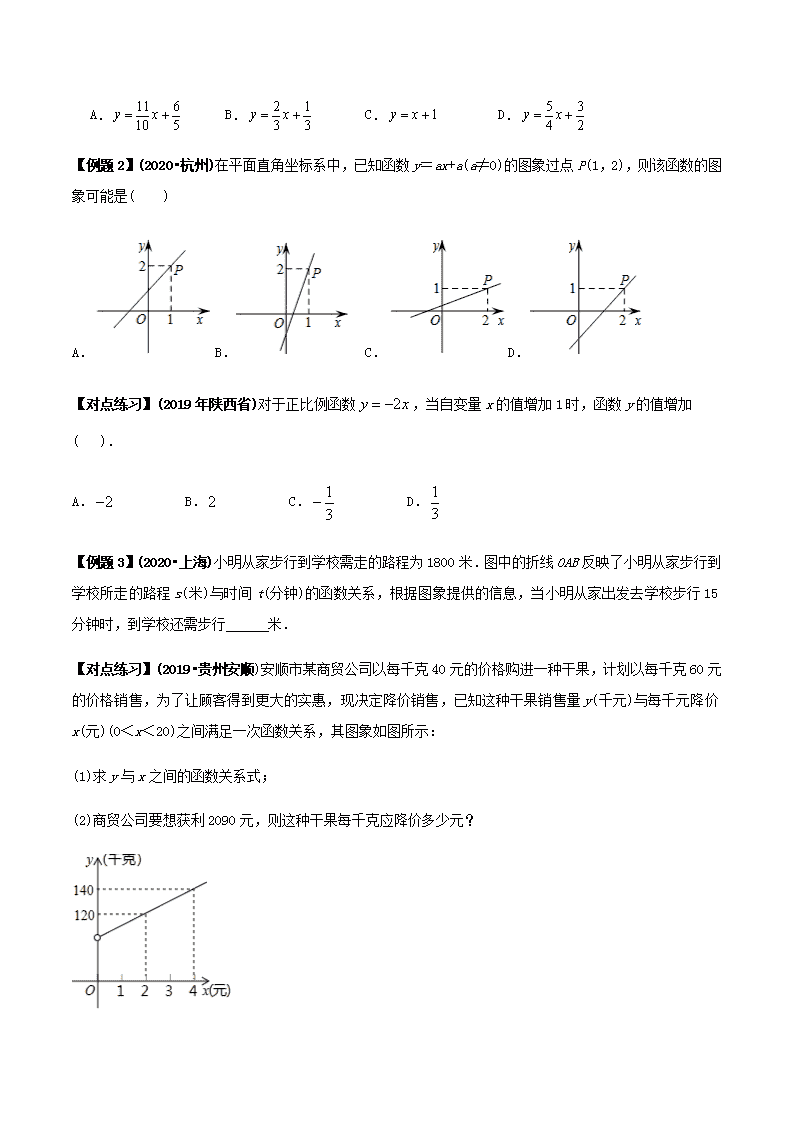【例题 1】(2020 贵州黔西南)如图，正比例函数的图象与一次函数 y＝－x＋1 的图象相交于点 P，点 P 到 x 轴的距离是 2，则这个正比例函数的解析式是________． 【对点练习】(2019 广西桂林)如图，四边形 ABCD 的顶点坐标分别为 ( 4,0)A  ， ( 2, 1)B   ， (3,0)C ， (0,3)D ， 当过点 B 的直线 l 将四边形 ABCD 分成面积相等的两部分时，直线 l 所表示的函数表达式为 ( ) A． 11 6 10 5 y x  B． 2 1 3 3 y x  C． 1y x  D． 5 3 4 2 y x  【例题 2】(2020•杭州)在平面直角坐标系中，已知函数 y＝ax+a(a≠0)的图象过点 P(1，2)，则该函数的图 象可能是( ) A． B． C． D． 【对点练习】(2019 年陕西省)对于正比例函数 2y x  ，当自变量 x 的值增加 1时，函数 y 的值增加( )． A． 2 B．2 C． 1 3  D． 1 3 【例题 3】(2020•上海)小明从家步行到学校需走的路程为 1800 米．图中的折线 OAB 反映了小明从家步行到 学校所走的路程 s(米)与时间 t(分钟)的函数关系，根据图象提供的信息，当小明从家出发去学校步行 15 分钟时，到学校还需步行 米． 【对点练习】(2019•贵州安顺)安顺市某商贸公司以每千克 40 元的价格购进一种干果，计划以每千克 60 元 的价格销售，为了让顾客得到更大的实惠，现决定降价销售，已知这种干果销售量 y(千元)与每千元降价 x(元)(0＜x＜20)之间满足一次函数关系，其图象如图所示： (1)求 y 与 x 之间的函数关系式； (2)商贸公司要想获利 2090 元，则这种干果每千克应降价多少元？ 【例题 4】(2020•北京)在平面直角坐标系 xOy 中，一次函数 y＝kx+b(k≠0)的图象由函数 y＝x 的图象平移 得到，且经过点(1，2)． (1)求这个一次函数的解析式； (2)当 x＞1 时，对于 x 的每一个值，函数 y＝mx(m≠0)的值大于一次函数 y＝kx+b 的值，直接写出 m的取值 范围． 【对点练习】(2019•上海)在平面直角坐标系 xOy 中(如图)，已知一次函数的图象平行于直线 y＝ x，且经 过点 A(2，3)，与 x轴交于点 B． (1)求这个一次函数的解析式； (2)设点 C在 y轴上，当 AC＝BC 时，求点 C 的坐标． 一、选择题 1．(2020•甘孜州)函数 y 香䁕 中，自变量 x 的取值范围是( ) A．x＞﹣3 B．x＜3 C．x≠﹣3 D．x≠3 2．(2020•内江)将直线 y＝﹣2x﹣1 向上平移两个单位，平移后的直线所对应的函数关系式为( ) A．y＝﹣2x﹣5 B．y＝﹣2x﹣3 C．y＝﹣2x+1 D．y＝﹣2x+3 3．(2020•凉山州)若一次函数 y＝(2m+1)x+m﹣3 的图象不经过第二象限，则 m的取值范围是( ) A．m＞ B．m＜3 C． ＜m＜3 D． ＜m≤3 4.(2020•菏泽)函数 y ‷ 的自变量 x的取值范围是( ) A．x≠5 B．x＞2且 x≠5 C．x≥2 D．x≥2且 x≠5 5．(2020•安徽)如图，△ABC 和△DEF 都是边长为 2 的等边三角形，它们的边 BC，EF 在同一条直线 l 上， 点 C，E 重合．现将△ABC 在直线 l 向右移动，直至点 B与 F 重合时停止移动．在此过程中，设点 C 移动的 距离为 x，两个三角形重叠部分的面积为 y，则 y 随 x 变化的函数图象大致为( ) A． B． C． D．6.(2019•江苏扬州)若点 P 在一次函数 4 xy 的图像上，则点 P 一 定不在( ) A.第一象限 B. 第二象限 C. 第三象限 D. 第四象限 7.(2019 贵州省毕节市)已知一次函数 y＝kx+b(k，b 为常数，k≠0)的图象经过一、三、四象限，则下列结 论正确的是( ) A．kb＞0 B．kb＜0 C．k+b＞0 D．k+b＜0 8.(2019 广西梧州)直线 3 1y x  向下平移 2个单位，所得直线的解析式是 ( ) A． 3 3y x  B． 3 2y x  C． 3 2y x  D． 3 1y x  9.(2019 湖南邵阳)一次函数 1 1 1y k x b  的图象 1l 如图所示，将直线 1l 向下平移若干个单位后得直线 2l ， 2l 的 函数表达式为 2 2 2y k x b  ．下列说法中错误的是 ( ) A． 1 2k k B． 1 2b b C． 1 2b b D．当 5x  时， 1 2y y 10.(2019•浙江杭州)已知一次函数 y1＝ax+b 和 y2＝bx+a(a≠b)，函数 y1和 y2的图象可能是( ) A B C D 二、填空题 11．(2020•黑龙江)在函数 y 䁕 中，自变量 x 的取值范围是 ． 12．(2020•上海)已知 f(x) ，那么 f(3)的值是 ． 13．(2020•黔东南州)把直线 y＝2x﹣1 向左平移 1 个单位长度，再向上平移 2 个单位长度，则平移后所得 直线的解析式为 ． 14．(2020•遵义)如图，直线 y＝kx+b(k、b 是常数 k≠0)与直线 y＝2 交于点 A(4，2)，则关于 x 的不等式 kx+b＜2 的解集为 ． 15.(2020•绥化)黑龙江省某企业用货车向乡镇运送农用物资，行驶 2 小时后，天空突然下起大雨，影响车 辆行驶速度，货车行驶的路程 y(km)与行驶时间 x(h)的函数关系如图所示，2 小时后货车的速度是 km/h． 16.(2019•江苏无锡)已知一次函数 y＝kx+b 的图象如图所示，则关于 x 的不等式 3kx﹣b＞0 的解 集为 ． 17.(2019•贵阳)在平面直角坐标系内，一次函数 y＝k1x+b1与 y＝k2x+b2的图象如图所示，则关于 x，y 的方 程组 的解是 ． 18.(2019 贵州黔西南州)如图所示，一次函数 y＝ax+b(a、b 为常数，且 a＞0)的图象经过点 A(4，1)，则不 等式 ax+b＜1 的解集为 ． 19. (2019 山东东营)如图，在平面直角坐标系中，函数y= 3 3 x 和 y=－ 3 x 的图象分别为直线 l1，l2，过 l1 上的点 A1(1， 3 3 )作 x 轴的垂线交 l2于点 A2，过点 A2作 y轴的垂线交 l1于点 A3，过点 A3作 x 轴的垂线交 l2于点 A4，…依次进行下去，则点 A2019的横坐标为____________． 20.(2019 江苏徐州)函数 y＝x＋1的图像与 x轴、y 轴分别交于 A、B 两点，点 C 在 x 轴上，若△ABC 为等腰 三角形，则满足条件的点 C 共有_________个. 三、解答题 21．(2020•嘉兴)经过实验获得两个变量 x(x＞0)，y(y＞0)的一组对应值如下表． x 1 2 3 4 5 6 y 6 2.9 2 1.5 1.2 1 (1)请画出相应函数的图象，并求出函数表达式． (2)点 A(x1，y1)，B(x2，y2)在此函数图象上．若 x1＜x2，则 y1，y2有怎样的大小关系？请说明理由． 22.(2020 浙江绍兴)我国传统的计重工具﹣﹣秤的应用，方便了人们的生活．如图 1，可以用秤砣到秤纽的 水平距离，来得出秤钩上所挂物体的重量．称重时，若秤杆上秤砣到秤纽的水平距离为 x(厘米)时，秤钩所 挂物重为 y(斤)，则 y 是 x 的一次函数．下表中为若干次称重时所记录的一些数据． x(厘米) 1 2 4 7 11 12 y(斤) 0.75 1.00 1.50[] 2.75 3.25 3.50 (1)在上表 x，y 的数据中，发现有一对数据记录错误．在图 2 中，通过描点的方法，观察判断哪一对是错 误的？ (2)根据(1)的发现，问秤杆上秤砣到秤纽的水平距离为 16 厘米时，秤钩所挂物重是多少？ 23.(2020•武威)通过课本上对函数的学习，我们积累了一定的经验．下表是一个函数的自变量 x 与函数值 y 的部分对应值，请你借鉴以往学习函数的经验，探究下列问题： x … 0 1 2 3 4 5 … y … 6 3 2 1.5 1.2 1 … (1)当 x＝ 时，y＝1.5； (2)根据表中数值描点(x，y)，并画出函数图象； (3)观察画出的图象，写出这个函数的一条性质： ． 24．(2020•贵阳)第 33 个国际禁毒日到来之际，贵阳市策划了以“健康人生 绿色无毒”为主题的禁毒宣传 月活动，某班开展了此项活动的知识竞赛．学习委员为班级购买奖品后与生活委员对话如下： (1)请用方程的知识帮助学习委员计算一下，为什么说学习委员搞错了； (2)学习委员连忙拿出发票，发现的确错了，因为他还买了一本笔记本，但笔记本的单价已模糊不清，只能 辨认出单价是小于 10 元的整数，那么笔记本的单价可能是多少元？