中考数学专题复习练习：全等三角形 10页

全等三角形 一、全等三角形知识梳理:‎ 全等三角形的概念：能够完全重合的两个三角形；‎ 全等三角形的性质：全等三角形对应边；对应角相等；对应边上的中线相等；对应边上的高相等；对应角的平分线相等. ‎ 三角形全等的条件：（1）SSS; (2) SAS; (3) ASA; (4) AAS; (5) HL 两个三角形不全等的情况：（1）有两边和其中一边的对角对应相等的两个三角形；‎ ‎ （2）有三个角对应相等的两个三角形.‎ 全等变换：只改变图形的位置，而不改变其形状大小的图形变换叫全等变换.平移、翻折、旋转前后的图形全等，具有全等的所有性质.‎ ‎（1）平移变换：把图形沿某直线平行移动.‎ ‎（2）对称变换：将图形沿直线翻着1800.‎ ‎（3）旋转变换：将图形绕某点旋转一定的角度到另一个位置.‎ 二、角平分线：‎ 角平分线的定义：一条射线，把一个角分成两个相等的角，这条射线叫做这个角的角平分线.‎ 角平分线的性质：角平分线上的点到角的两边的举距离相等.到角两边距离相等的点在角的角平分线上.‎ 三角形角平分线性质：三角形三条角平分线交于三角形内部一点，并且交点到三边距离相等.‎ 三、几何证明的一般步骤：‎ ‎1. 根据题意，画出图形；‎ ‎2. 根据题设、结论、，结合图形，写出已知、求证.‎ ‎3. 经过分析，找出由已知推出求证的途径，写出证明过程.‎ 考点分析 ‎1. 全等的概念和性质；‎ ‎2．三角形全等的条件：只给出三角形三角三边六个条件中的一个或两个条件时，都不能保证所画出的三角形一定全等.‎ ‎3. 全等三角形的利用：‎ 证明角相等：（1）对顶角相等；（2）等角的余角（或补角）相等；（3）两直线平行，同位角相等，内错角相等；（4）角平分线的定义；（5）等式性质；（6）全等三角形的对应角相等；（7）等边对等角.‎ 证明线段线段：（1）中点定义；（2）等式性质；（3）全等三角形的对应边相等；（4）等角对等边；（5）角平分线的性质.‎ 证明垂直的方法：（1）证明两直线夹角等于900；（2）证明邻补角相等；（3）若三角形的两锐互余，则第三 个角是直角；（4）垂直于平行线中的一条直线也垂直于另一条直线；（5）证明该角所在的三角 形与已知直角三角形全等；（6）邻补角的平分线互相垂直.‎ 证明一条线段等于另外两条线段的和：采用截长补短法. （1）截长法：在较长的线段上截取一条线段等于较短线段；（2）补短法：延长较短线段和较长线段相等.‎ ‎4. 角平分线的性质及相关证明；‎ ‎（1）有角平分线时，常用角平分线上的点向角两边作垂线段，利用角平分线上的点到角两边距离相等证题.‎ ‎（2）有角平分线时，通常在角的两边截取相等的线段，构造全等三角形.‎ ‎5. 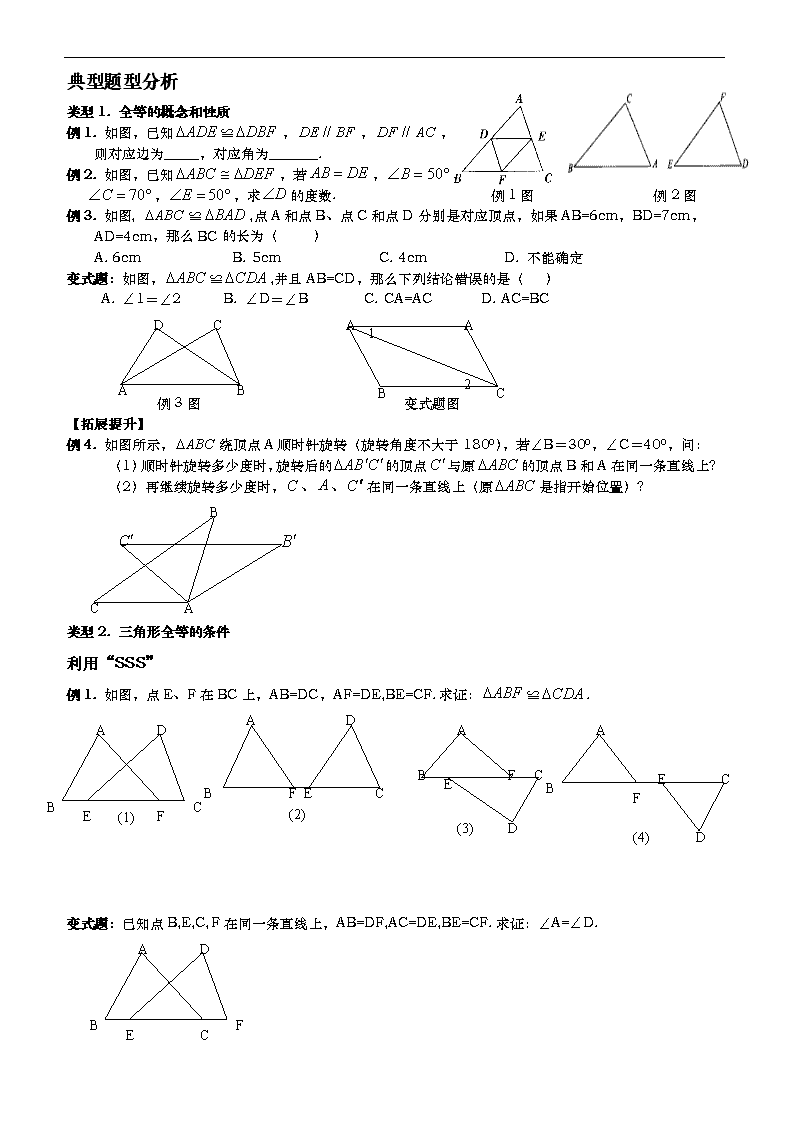中线的性质相关证明：‎ ‎（1）取线段中点构造全等三有形；‎ ‎（2）有以线段中点为端点的线段时，常延长加倍此线段，构造全等三角形；‎ ‎（3）有三角形中线时，常延长加倍中线，构造全等三角形 (倍长中线).‎ 典型题型分析 类型1. 全等的概念和性质 例1. 如图，已知≌，，，‎ 则对应边为_____，对应角为_______.‎ 例2. 如图，已知，若，，‎ ‎，，求的度数. 例1图 例2图 例3. 如图, ≌,点A和点B、点C和点D分别是对应顶点，如果AB=6cm，BD=7cm，AD=4cm，那么BC的长为（ ） ‎ A. 6cm B. 5cm C. 4cm D. 不能确定 变式题：如图，≌,并且AB=CD，那么下列结论错误的是（ ） ‎ A. ∠1＝∠2 B. ∠D＝∠B C. CA=AC D. AC=BC B ‎ C ‎ A ‎ AD ‎ ‎1 ‎ ‎22 ‎ D ‎ C ‎ B ‎ A ‎ ‎ 例3图 变式题图 ‎【拓展提升】‎ 例4. 如图所示，绕顶点A顺时针旋转（旋转角度不大于1800），若∠B＝300，∠C＝400，问：‎ ‎（1）顺时针旋转多少度时，旋转后的的顶点与原的顶点B和A在同一条直线上？‎ ‎ （2）再继续旋转多少度时，、、在同一条直线上（原是指开始位置）？‎ C ‎ A ‎ ‎ ‎ B ‎ ‎ ‎ 类型2. 三角形全等的条件 利用“SSS”‎ 例1. 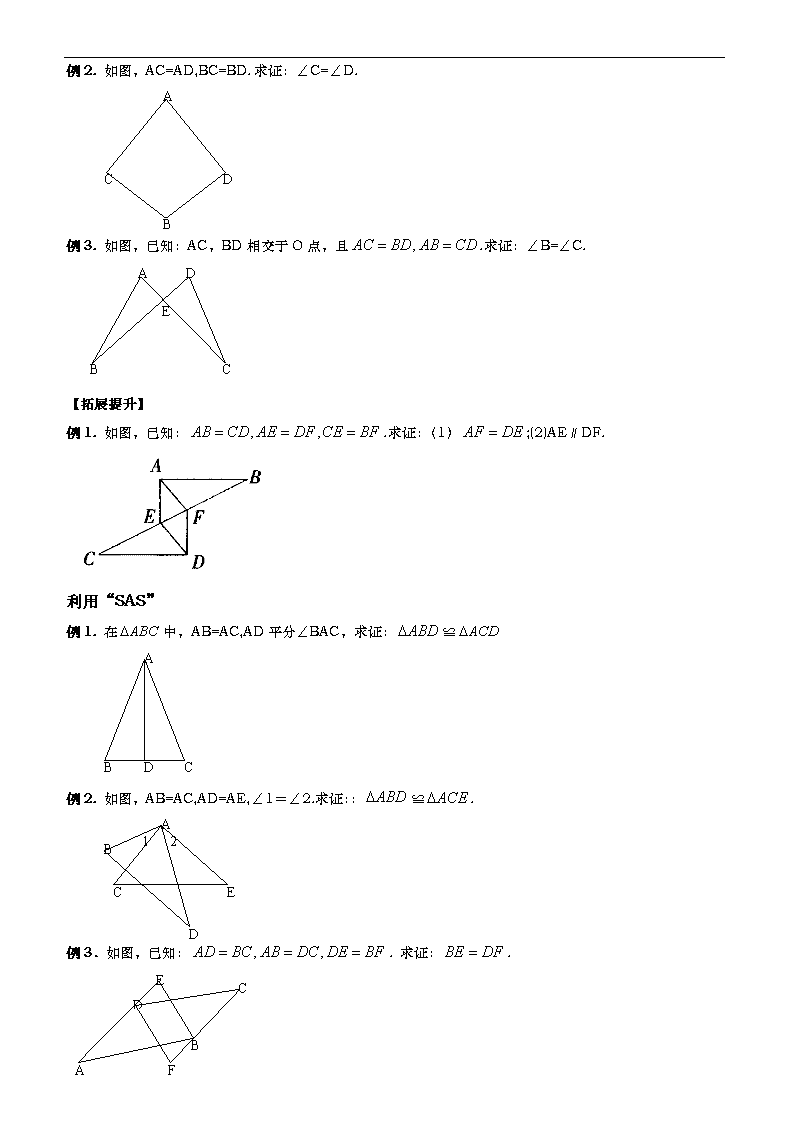如图，点E、F在BC上，AB=DC，AF=DE,BE=CF.求证：≌.‎ A ‎ D ‎ B ‎ E ‎ F ‎ C ‎ ‎(1) ‎ A ‎ BB ‎ F ‎ E ‎ D ‎ C ‎ ‎(2) ‎ A ‎ B ‎ F ‎ E ‎ C ‎ D ‎ ‎(4) ‎ A ‎ B ‎ E ‎ F ‎ D ‎ C ‎ ‎(3) ‎ ‎ ‎ 变式题：已知点B,E,C,F在同一条直线上，AB=DF,AC=DE,BE=CF.求证：∠A=∠D.‎ A ‎ D ‎ B ‎ E ‎ C ‎ F ‎ ‎ ‎ 例2. 如图，AC=AD,BC=BD.求证：∠C=∠D.‎ B ‎ D ‎ C ‎ A ‎ A ‎ D ‎ B ‎ C ‎ E ‎ 例3. 如图，已知：AC，BD相交于O点，且.求证：∠B=∠C.‎ ‎【拓展提升】‎ 例1. 如图，已知：.求证：（1）;(2)AE∥DF. ‎ 利用“SAS”‎ 例1. 在中，AB=AC,AD平分∠BAC，求证：≌‎ A ‎ B ‎ C ‎ D ‎ 例2. 如图，AB=AC,AD=AE,∠1＝∠2.求证：：≌.‎ A ‎ B ‎ C ‎ D ‎ E ‎ ‎1 ‎ ‎2 ‎ ‎ ‎ A ‎ F ‎ D ‎ B ‎ C ‎ EE ‎ 例3．如图，已知：. 求证：. ‎ ‎【拓展提升】‎ 例1. 如图，已知： ，求证：‎ 例2. 如图，已知：，. 求证：. ‎ 利用：“ASA” “ASA”‎ 例1. 由AB⊥BD,ED⊥BD,垂足分别为B、D点，点C在BD上，且BC=CD,点A、C、E在同一条直线上，求证：DE=AB.‎ A ‎ BBB ‎ E ‎ D ‎ C ‎ G ‎ F ‎ 例2. 和中，∠A=500, ∠B=300,AB=10, ∠B=500, ∠F=1000,DE=10,‎ 求证：≌‎ 变式题：如图, ∠ABC=∠DCB, ∠ACB=∠DBC,求证：AC=DB.‎ A ‎ B ‎ C ‎ DD ‎ 例3. 如图，在ΔAFD和ΔCEB中，点A、E、F、C在同一条直线上，有下面四个论断：（1）AD=CB,(2)AF=CE,‎ ‎(3) ∠B=∠D ,(4) AD∥BC.请用其中三个条件，余下一个作为结论，编一道数学题并写出解答过程.‎ A ‎ D ‎ BBB ‎ CC ‎ E ‎ F ‎ 例4. 如图，已知：. 求证：. ‎ 例5. 如图，两条直线AC,BD相交于O，BO=DO,AO=CO，直线EF过点O且分别交AB、CD于 点E,F，求证：OE=OF D ‎ F ‎ C ‎ O ‎ A ‎ E ‎ B ‎ 例6. 如图，已知：，.求证：点B是线段AC的中点.‎ 例7.如图，已知：，，，直线DC过E点交AD于D，交BC于C.‎ 求证：.‎ ‎【拓展提升】‎ 例1. 如图，已知：，.求证：.‎ 例2. 如图，已知： AD为的高，且，F为AD上一点，连结BF并延长交AC于E，.‎ ‎ 求证：‎ 例3. 如图所示：在△ABC和△DBC中，∠ACB=∠DBC=,E是BC的中点，EF⊥AB,垂足为F，‎ 且AB=DE. （1）求证：BD=BC; （2）若BD=8cm，求AC的长.‎ C ‎ E ‎ B ‎ A ‎ F ‎ D ‎ 例4. 某人在河的一岸，要测河面一只船B与码头A距离，他的做法是：（1）在岸边确定一点C，使C与A、B在同一直线上，（2）在AC的垂直方向画线段CD，取其中点O，（3）画DF⊥CD，使F、O、A在同一直线上，（4）在线段DF上找到一点E，使E与O、B共线.他说只要测出线段EF的长就是船B与码头A的距离.他这样做有道理吗？为什么？‎ A ‎ C ‎ B ‎ DD ‎ E ‎ F ‎ O ‎ 例5. 如图，在△ABC中，AC⊥BC,AC=BC,D为AB上一点，AF⊥CD交CD的延长线于F，BE⊥CD 于E.求证：EF=BE—AF A ‎ C ‎ F ‎ D ‎ E ‎ BB ‎ 利用：“HL”‎ 例1. 如图，已知AB=CD，DE⊥AC,BF⊥AC,DE=BF，求证：AB∥CD.‎ D ‎ A ‎ E ‎ F ‎ B ‎ C ‎ B ‎ F ‎ G ‎ C ‎ D ‎ E ‎ A ‎ 例2. 如图，△ABC中，点D、E分别是AB、AC边上的点，BD=CE，DF⊥BC于点F,EG⊥BC,于点G，且DF=EG.求证：BE=CD.‎ 例3．如图，AB=AC,点D、E分别在AC、AB上，AG⊥BD,AF⊥CE,垂足分别为G、F，且AG=AF.‎ ‎ 求证：AD=AE.‎ BB ‎ C ‎ A ‎ E ‎ D ‎ F ‎ G ‎ ‎【拓展提升】‎ 例1. 已知，如图，△ABC和都是锐角三角形，CD、分别是高，且,‎ ‎ ,.求证：△ABC ≌.‎ A ‎ D ‎ B ‎ C ‎ A ‎ D ‎ B ‎ C ‎ 变式题：如果△ABC和都是钝角三角形，其余条件不变，结论：“△ABC ≌”还成立吗？‎ 如图，已知：,.求证：点B是线段AC的中点.‎ 巩固练习：‎ ‎1. 如图，已知：求证：. ‎ ‎2. 如图，已知：求证：.‎ ‎3. 如图，已知：D、E是BC上的两点，且求证：.‎ ‎4．已知：在中，M在BC上，D在AM上，（如图）求证：‎ ‎5. 如图所示，已知，E是AC上一点. 求证：. ‎ A ‎ D ‎ CC ‎ B ‎ ‎6. 如图，已知：.求证：.‎ ‎7. 已知：（如图）. 求证：‎ 变式题：如图，已知，，.求证：.‎ ‎8. 如图，已知：，直线AE，BD相交于点C，，，交BD于F.‎ 求证：.‎ ‎9. 如图，已知：，EF过点O.求证：.‎ ‎10. 如图，已知：在中，AD是的平分线，于E，于C，求证：.‎ C ‎ D ‎ A ‎ E ‎ F ‎ B ‎ ‎11. 如图：AC⊥BC,AD⊥BD,AD=BC,CE⊥AB,DF⊥AB,垂足分别是E,F，求证：CE=DF.‎