第章第节垂直于弦的直径导学案 4页

‎《圆》第一节 垂直于弦的直径导学案1‎ 主编人： 主审人：‎ 班级： 学号： 姓名： ‎ 学习目标：‎ ‎【知识与技能】‎ ‎1理解圆的轴对称性，掌握垂径定理及其他结论 ‎2学会运用垂径定理及其推论解决一些有关证明、计算和作图问题 ‎3了解拱高、弦心距等概念 ‎【过程与方法】‎ 经历探索发现圆的对称性，证明垂径定理及其他结论的过程，锻炼思维品质，学习证明的方法 ‎【情感、态度与价值观】‎ 在学生通过观察、操作、变换、探究出图形的性质后，还要求对发现的性质进行证明，培养学生的 新意识，良好的运用数学 ‎【重点】‎ 垂径定理及其推论 ‎【难点】‎ 垂径定理及其推论 学习过程:‎ 一、自主学习 ‎（一）复习巩固 ‎ 判断：‎ ‎1、直径是弦，弦是直径。 （ ） 2、半圆是弧，弧是半圆。 （ ）‎ ‎3、周长相等的两个圆是等圆。 （ ） 4、长度相等的两条弧是等弧。 （ ）‎ ‎5、同一条弦所对的两条弧是等弧。（ ） 6、在同圆中，优弧一定比劣弧长。（ ）‎ ‎7、请在图上画出弦CD，直径AB.并说明___________________________叫做弦；‎ ‎_________________________________ 叫做直径.‎ ‎8、在图上画出弧、半圆、优弧与劣弧并填出概念及表示方法.弧：___ _ ‎ 半圆：_________________________ 优弧：________________ _ 表示方法：__ ‎ 劣弧：______________________________ _,表示方法：______ ‎ ‎9、同心圆: __________________ _ _等圆: __________________________ _. ‎ ‎10、同圆或等圆的半径_______.等弧: _______________________ ‎ ‎（二）自主探究 请同学按下面要求完成下题：‎ 如图，AB是⊙O的一条弦，作直径CD，使CD⊥AB，垂足为M．‎ ‎（1）如图是轴对称图形吗？如果是，其对称轴是什么？‎ 4‎ 圆是 对称图形，其对称轴是任意一条过 的直线． ‎ ‎（2）你能发现图中有哪些相等的线段和弧？为什么？‎ ‎ 相等的线段： ‎ ‎ ‎ 相等的弧： ‎ ‎ ‎ ‎ ‎ ‎ 这样，我们就得到垂径定理：‎ 垂直于 的直径平分弦，并且平分弦所对的两条 ．‎ 表达式： ‎ ‎ ‎ ‎ ‎ 下面我们用逻辑思维给它证明一下：‎ ‎ 已知：直径CD、弦AB且CD⊥AB垂足为M ‎ 求证：AM=BM，弧AC=BC，弧AD=BD.‎ ‎ 分析：要证AM=BM，只要证AM、BM构成的两个三角形全等．因此，只要连结OA、OB或AC、BC即可．‎ 证明：如图，连结OA、OB，则OA=OB 在Rt△OAM和Rt△OBM中 ‎ ‎ ‎ ‎ ‎ ∴Rt△OAM≌Rt△OBM( )‎ ‎ ∴AM= ‎ D ‎ ∴点 和点 关于CD对称 ‎ ∵⊙O关于CD对称 ‎ ∴当圆沿着直线CD对折时，点A与点B重合，弧AC与BC重合，AD与CD重合．‎ ‎∴ ， ， ‎ ‎ 进一步，我们还可以得到结论：‎ 平分弦（ ）的直径垂直于 ，并且平分弦所对的两条 ．‎ 表达式： ‎ ‎ ‎ ‎（三）、归纳总结：‎ ‎ 1．圆是 图形，任何一条 所在直线都是它的对称轴．‎ ‎2．垂径定理 ‎ 推论 ．‎ ‎（四）自我尝试：‎ ‎1、辨析题：下列各图，能否得到AE=BE的结论？为什么？‎ C O O O E E B O A A B E B A D D A E B D R E D B A C ‎2、赵州桥的桥拱是圆弧形，它的跨度（弧所对的弦的长）为‎37.4m 4‎ ‎，拱高（弧的中点到弦的距离）为‎7.2m，你能求出赵州桥的主桥拱的半径吗？‎ 注：在半径r,弦a，弦心距d,拱高h四个量中，任意知道其中的 个量中，‎ 利用 定理，就可以求出其余的量。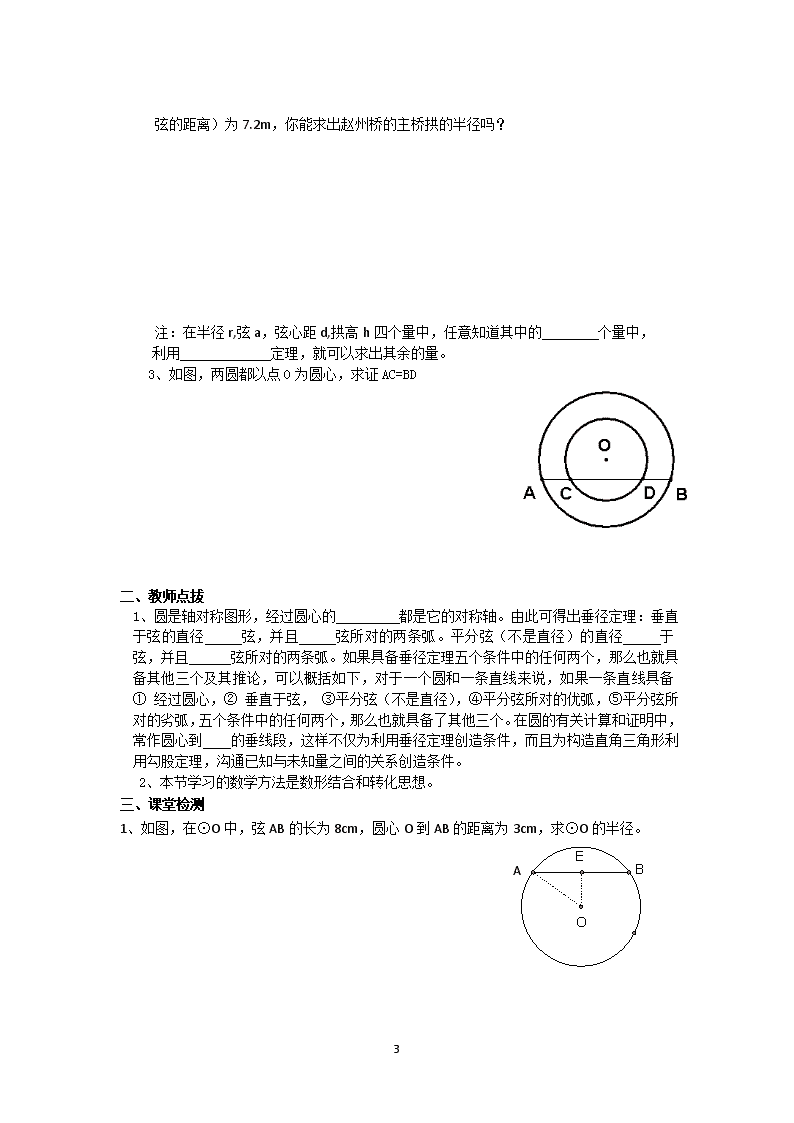‎ ‎3、如图，两圆都以点O为圆心，求证AC=BD 二、教师点拔 ‎1、圆是轴对称图形，经过圆心的 都是它的对称轴。由此可得出垂径定理：垂直于弦的直径 弦，并且 弦所对的两条弧。平分弦（不是直径）的直径 于弦，并且 弦所对的两条弧。如果具备垂径定理五个条件中的任何两个，那么也就具备其他三个及其推论，可以概括如下，对于一个圆和一条直线来说，如果一条直线具备① 经过圆心，② 垂直于弦， ③平分弦（不是直径），④平分弦所对的优弧，⑤平分弦所对的劣弧，五个条件中的任何两个，那么也就具备了其他三个。在圆的有关计算和证明中，常作圆心到 的垂线段，这样不仅为利用垂径定理创造条件，而且为构造直角三角形利用勾股定理，沟通已知与未知量之间的关系创造条件。‎ ‎ 2、本节学习的数学方法是数形结合和转化思想。‎ 三、课堂检测 O A B E ‎1、如图，在⊙O中，弦AB的长为‎8cm，圆心O到AB的距离为‎3cm，求⊙O的半径。‎ 4‎ ‎2、如图，在⊙O中，AB，AC为互相垂直且相等的两条弦，OD⊥AB于D，OE⊥AC于E，求证四边形ADOE是正方形。‎ O B A C E D 四、课外训练 ‎1．P为⊙O内一点，OP=‎3cm，⊙O半径为‎5cm，则经过P点的最短弦长为________；最长弦长为_______．‎ ‎2．如图5，OE、OF分别为⊙O的弦AB、CD的弦心距，如果OE=OF，那么_______（只需写一个正确的结论）‎ ‎ ‎ ‎ (5) （6）‎ ‎3．如图6，⊙O直径AB和弦CD相交于点E，AE=2，EB=6，∠DEB=30°，则弦CD长 ‎ ‎4.如图，一条公路的转弯处是一段圆弦（即图中CD，点O是CD弧所在圆的圆心，其中CD=‎300m，E为CD弧上一点，且OE⊥CD，垂足为F，EF=‎45m，求这段弯路的半径．‎ ‎ ‎ M M O A B C D ‎5.AB和CD分别是⊙O上的两条弦，圆心O到它们的距离分别是OM和ON，如果AB＞CD，OM和ON的大小有什么关系？为什么？‎ 4‎