2008年山东省青岛市中考数学真题 7页

二○○八山东省青岛市初级中学学业水平考试 数 学 试 题 （考试时间：120 分钟；满分 120 分） 真情提示：亲爱的同学，欢迎你参加本次考试，祝你答题成功！ 1．请务必在指定位置填写座号，并将密封线内的项目填写清楚． 2．本试题共有 24 道题，其中 1—7 题为选择题，请将所选答案的标号，写在第 7 题后面给 出表格的相应位置上：8—14 题为填空题，请将做出的答案填写在第 14 题后面给出表格的 相应位置上；15—24 题请在试题给出的本题位置上做答． 一、选择题（本题满分 21 分，共有 7 道小题，每小题 3 分） 下列每小题都给出标号为 A，B，C，D 的四个结论，其中只有一个是正确的．每小题选对 得分；不选，选错或选出的标号超过一个的不得分，请将 1—7 各小题所选答案的标号填写 在第 7 小题后面表格的相应位置上． 1． 1 4 的相反数等于（ ） A． 1 4 B． 1 4 C． 4 D． 4 2．下列图形中，轴对称图形的个数是（ ） Ａ．1 Ｂ．2 Ｃ．3 Ｄ．4 3．已知 1O 和 2O 的半径分别为 3cm 和 2cm，圆心距 12 4OO  cm，则两圆的位置关系是 （ ） A．相切 B．内含 C．外离 D．相交 4．某几何体的三种视图如右图所示，则该几何体可能是（ ） A．圆锥体 B．球体 C．长方体 D．圆柱体 5．一个口袋中有 3 个黑球和若干个白球，在不允许将球倒出来数的前提下，小明为估计其 中的白球数，采用了如下的方法：从口袋中随机摸出一球，记下颜色，然后把它放回口袋中， 摇匀后再随机摸出一球，记下颜色， ，不断重复上述过程．小明共摸了 100 次，其中 20 次摸到黑球．根据上述数据，小明可估计口袋中的白球大约有（ ） A．18 个 B．15 个 C．12 个 D．10 个 6．如果点 11()A x y， 和点 22()B x y， 是直线 y kx b上的两点，且当 12xx 时， 12yy ， 那么函数 ky x 的图象大致是（ ） 主视图 左视图 俯视图 y x O y x O y x O y x O A． B． C． D． 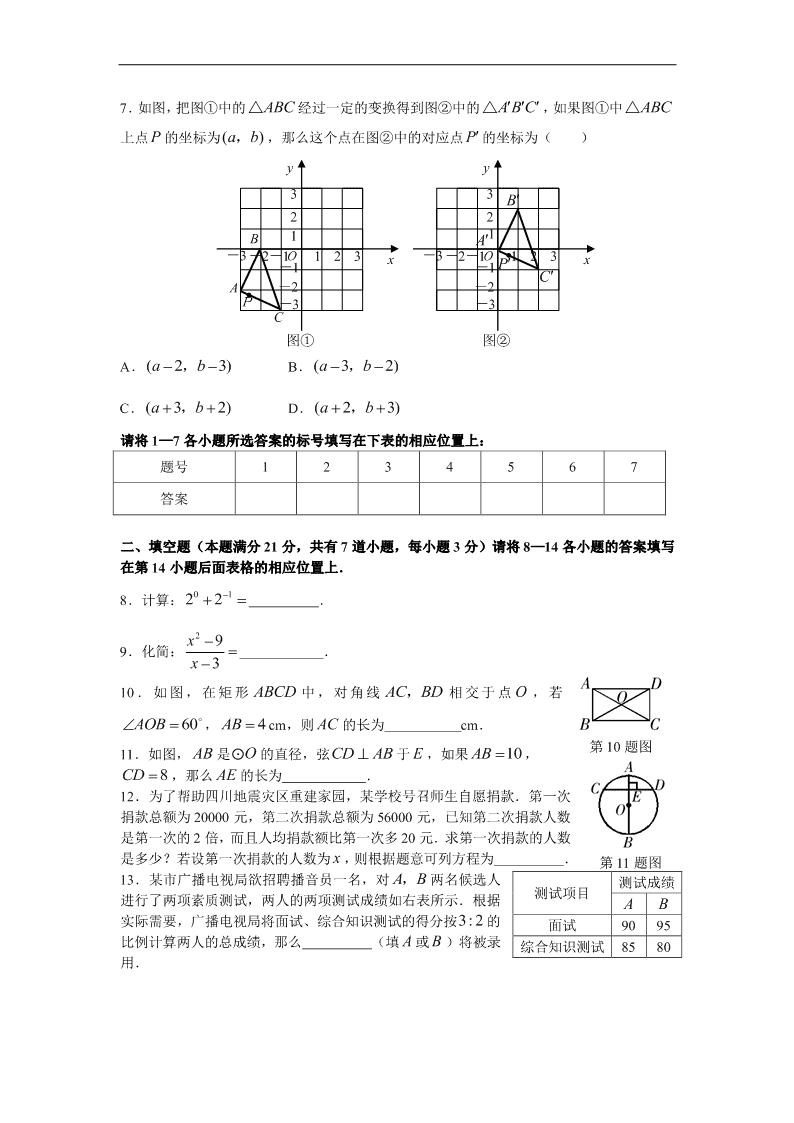7．如图，把图①中的 ABC△ 经过一定的变换得到图②中的 ABC  △ ，如果图①中 ABC△ 上点 P 的坐标为()ab， ，那么这个点在图②中的对应点 P的坐标为（ ） A．( 2 3)ab， B．( 3 2)ab， C．( 3 2)ab， D．( 2 3)ab， 请将 1—7 各小题所选答案的标号填写在下表的相应位置上： 题号 1 2 3 4 5 6 7 答案 二、填空题（本题满分 21 分，共有 7 道小题，每小题 3 分）请将 8—14 各小题的答案填写 在第 14 小题后面表格的相应位置上． 8．计算： 0122 ． 9．化简： 2 9 3 x x   ． 10 ． 如图，在矩形 ABCD中 ， 对 角 线 AC BD， 相交于点O ，若 60AOB， 4AB  cm，则 AC 的长为 cm． 11．如图， AB 是 O 的直径，弦CD AB 于 E ，如果 10AB  ， 8CD  ，那么 AE 的长为 ． 12．为了帮助四川地震灾区重建家园，某学校号召师生自愿捐款．第一次 捐款总额为 20000 元，第二次捐款总额为 56000 元，已知第二次捐款人数 是第一次的 2 倍，而且人均捐款额比第一次多 20 元．求第一次捐款的人数 是多少？若设第一次捐款的人数为 x ，则根据题意可列方程为 ． 13．某市广播电视局欲招聘播音员一名，对 AB， 两名候选人 进行了两项素质测试，两人的两项测试成绩如右表所示．根据 实际需要，广播电视局将面试、综合知识测试的得分按3: 2 的 比例计算两人的总成绩，那么 （填 A 或 B ）将被录 用． 测试项目 测试成绩 A B 面试 90 95 综合知识测试 85 80 3 2 1 －1 Ｏ －2 －3 －3 －2 －1 1 2 3 x y 图① 3 2 1 －1 Ｏ －2 －3 －3 －2 －1 1 2 3 x y 图② Ｐ A B C A B C P 第 10 题图 第 11 题图 14．如图是一个用来盛爆米花的圆锥形纸杯，纸杯开口圆的直径 EF 长为 10cm．母线 ()OE OF 长为 10cm．在母线OF 上的点 A 处 有一块爆米花残渣，且 2FA  cm，一只蚂蚁从杯口的点 E 处沿圆 锥表面爬行到 A 点．则此蚂蚁爬行的最短距离为 cm． 请将 8—14 各小题的答案填写在下表的相应位置上： 题号 8 9 10 11 答案 题号 12 13 14 答案 三、作图题（本题满分 6 分） 用圆规、直尺作图，不写作法，但要保留作图痕迹． 15．如图， AB AC， 表示两条相交的公路，现要在 BAC 的内部建一个物流中心．设计时 要求该物流中心到两条公路的距离相等，且到公路交叉处 A 点的距离为 1000 米． （1）若要以1:50000的比例尺画设计图，求物流中心到公路交叉处 A 点的图上距离； （2）在图中画出物流中心的位置 P ． 解：（1） 结论： 四、解答题（本题满分 72 分，共有 9 道小题） 16．（本小题满分 6 分） 用配方法解一元二次方程： 2 2 2 0xx   ． 17．（本小题满分 6 分） 某市为调查学生的视力变化情况，从全市九年级学生中抽取了部分学生，统计了每个人连续 三年视力检查的结果，并将所得数据处理后，制成折线统计图和扇形统计图如下： Ａ Ｆ Ｅ Ｏ 第 14 题图 A C B （2） 1cm 解答下列问题： （1）该市共抽取了多少名九年级学生？ （2）若该市共有 8 万名九年级学生，请你估计该市九年级视力不良（4.9 以下）的学生大约 有多少人？ （3）根据统计图提供的信息，谈谈自己的感想（不超过 30 字）． 18．（本小题满分 6 分） 小明和小刚用如图所示的两个转盘做配紫色游戏，游戏规则是：分别旋转两个转盘，若其中 一个转盘转出了红色，另一个转出了蓝色，则可以配成紫色．此时小刚得 1 分，否则小明得 1 分． 这个游戏对双方公平吗？请说明理由．若你认为不公平，如何修改规则才能使游戏对双方公 平？ 19．（本小题满分 6 分） 在一次课题学习课上，同学们为教室窗户设计一个遮阳蓬，小明同学绘制的设计图如图所示， 其中 AB 表示窗户，且 2AB  米， BCD表示直角遮阳蓬，已知当地一年中在午时的太阳 光与水平线CD 的最小夹角 为18.6 ，最大夹角  为64.5 ． 请你根据以上数据，帮助小明同学计算出遮阳蓬中CD 的长是多少米？（结果保留三个有效 数字） （参考数据：sin18.6 0.32 ， tan18.6 0.34 ，sin64.5 0.90 ， tan64.5 2.1 ） 人数 时间（年） 800 500 300 0 2006 2007 2008 被抽取学生视力在 4.9 以下 的人数变化情况统计图 A 40% B 30% C 20% D 10% A：4.9 以下 B：4.9－5.1 C：5.1－5.2 D：5.2 以上 （ 每 组 数 据 只含最 低 值 不含最高值） 被抽取学生 2008 年的视 力分布情况统计图 红 黄 蓝 红 白 蓝 20．（本小题满分 8 分） 2008 年 8 月，北京奥运会帆船比赛将在青岛国际帆船中心举行．观看帆船比赛的船票分为 两种：A 种船票 600 元/张，B 种船票 120 元/张．某旅行社要为一个旅行团代购部分船票， 在购票费不超过 5000 元的情况下，购买 A，B 两种船票共 15 张，要求 A 种船票的数量不少 于 B 种船票数量的一半．若设购买 A 种船票 x 张，请你解答下列问题： （1）共有几种符合题意的购票方案？写出解答过程； （2）根据计算判断：哪种购票方案更省钱？ 21．（本小题满分 8 分） 已知：如图，在正方形 ABCD中，G 是CD 上一点，延长 BC 到 E ，使 CE CG ，连接 BG 并延长交 DE 于 F ． （1）求证： BCG DCE△ ≌△ ； （2）将 DCE△ 绕点 D 顺时针旋转90 得到 DAE△ ， 判断四边形 E BGD 是什么特殊四边形？并说明理由． 22．（本小题满分 10 分） 某服装公司试销一种成本为每件 50 元的 T 恤衫，规定试销时的销售单价不低于成本价，又 不高于每件 70 元，试销中销售量 y （件）与销售单价 x （元）的关系可以近似的看作一次 函数（如图）． （1）求 y 与 x 之间的函数关系式； （2）设公司获得的总利润（总利润 总销售额 总成本）为 P 元，求 P 与 x 之间的函数关 系式，并写出自变量 x 的取值范围；根据题意判断：当 x 取何值时，P 的值最大？最大值是 多少？ 400 300 60 70 Ｏ y(件) x(元) A D Ｄ Ｃ B  Ｄ  A B C D E F E G 23．（本小题满分 10 分） 实际问题：某学校共有 18 个教学班，每班的学生数都是 40 人．为了解学生课余时间上网情 况，学校打算做一次抽样调查，如果要确保全校抽取出来的学生中至少有 10 人在同一班级， 那么全校最少需抽取多少名学生？ 建立模型：为解决上面的“实际问题”，我们先建立并研究下面从口袋中摸球的数学模型： 在不透明的口袋中装有红、黄、白三种颜色的小球各 20 个（除颜色外完全相同），现要确保 从口袋中随机摸出的小球至少有 10 个是同色的，则最少需摸出多少个小球？ 为了找到解决问题的办法，我们可把上述问题简单化： （1）我们首先考虑最简单的情况：即要确保从口袋中摸出的小球至少有 2 个是同色的，则 最少需摸出多少个小球？ 假若从袋中随机摸出 3 个小球，它们的颜色可能会出现多种情况，其中最不利的情况就是它 们的颜色各不相同，那么只需再从袋中摸出 1 个小球就可确保至少有 2 个小球同色，即最少 需摸出小球的个数是：1 3 4（如图①）； （2）若要确保从口袋中摸出的小球至少有 3 个是同色的呢？ 我们只需在（1）的基础上，再从袋中摸出 3 个小球，就可确保至少有 3 个小球同色，即最 少需摸出小球的个数是：1 3 2 7   （如图②） （3）若要确保从口袋中摸出的小球至少有 4 个是同色的呢？ 我们只需在（2）的基础上，再从袋中摸出 3 个小球，就可确保至少有 4 个小球同色，即最 少需摸出小球的个数是：1 3 3 10   （如图③）： （10）若要确保从口袋中摸出的小球至少有 10 个是同色的呢？ 我们只需在（9）的基础上，再从袋中摸出 3 个小球，就可确保至少有 10 个小球同色，即最 少需摸出小球的个数是：1 3 (10 1) 28    （如图⑩） 模型拓展一：在不透明的口袋中装有红、黄、白、蓝、绿五种颜色的小球各 20 分（除颜色 外完全相同），现从袋中随机摸球： （1）若要确保摸出的小球至少有 2 个同色，则最少需摸出小球的个数是 ； （2）若要确保摸出的小球至少有 10 个同色，则最少需摸出小球的个数是 ； （3）若要确保摸出的小球至少有 n 个同色（ 20n  ），则最少需摸出小球的个数是 ． 模型拓展二：在不透明口袋中装有 m 种颜色的小球各 20 个（除颜色外完全相同），现从袋 中随机摸球： 红 黄 红 红或黄或白 图② 黄 白 白 红 黄 白 红或黄或白 图① 红 红 红或黄或白 图③ 红 白 白 白 黄 黄 黄 红 红 红或黄或白 图⑩ 红 白 白 白 黄 黄 黄 白 … 红 黄 9 个 9 个 9 个 ．．． （1）若要确保摸出的小球至少有 2 个同色，则最少需摸出小球的个数是 ． （2）若要确保摸出的小球至少有 n 个同色（ 20n  ），则最少需摸出小球的个数是 ． 问题解决：（1）请把本题中的“实际问题”转化为一个从口袋中摸球的数学模型； （2）根据（1）中建立的数学模型，求出全校最少需抽取多少名学生． 24．（本小题满分 12 分） 已知：如图①，在 Rt ACB△ 中， 90C ， 4cmAC  ， 3cmBC  ，点 P 由 B 出发 沿 BA 方向向点 A 匀速运动，速度为 1cm/s；点Q 由 A 出发沿 AC 方向向点C 匀速运动，速 度为 2cm/s；连接 PQ ．若设运动的时间为 (s)t （02t ），解答下列问题： （1）当t 为何值时， PQ BC∥ ？ （2）设 AQP△ 的面积为 y （ 2cm ），求 y 与t 之间的函数关系式； （3）是否存在某一时刻t ，使线段 PQ 恰好把 Rt ACB△ 的周长和面积同时平分？若存在， 求出此时t 的值；若不存在，说明理由； （4）如图②，连接 PC ，并把 PQC△ 沿QC 翻折，得到四边形 PQP C ，那么是否存在某 一时刻t ，使四边形 PQP C 为菱形？若存在，求出此时菱形的边长；若不存在，说明理由． A Q C P B 图① A Q C P B P 图②