九年级上册青岛版数学课件1-2怎样判定三角形相似（3） 21页

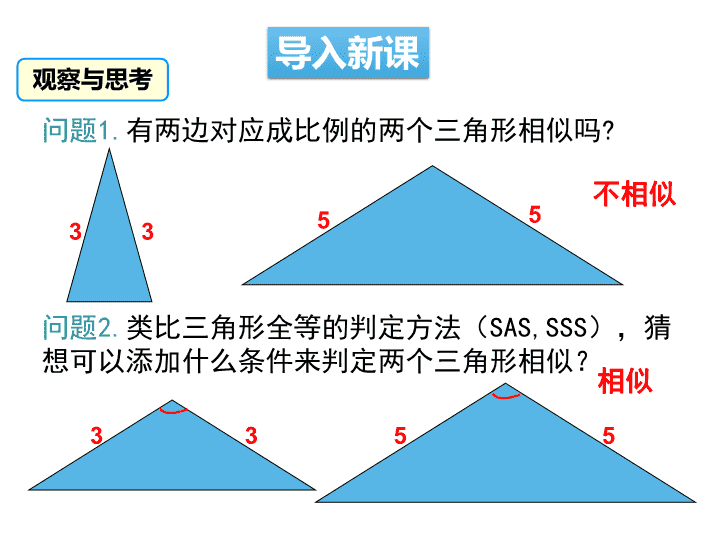
1.2怎样判定三角形相似（3） 1.掌握相似三角形的判定定理2；（重点） 2.能熟练运用相似三角形的判定定理2．（难点） 学习目标 问题1.有两边对应成比例的两个三角形相似吗? 3 3 55 不相似 观察与思考 问题2.类比三角形全等的判定方法（SAS,SSS），猜 想可以添加什么条件来判定两个三角形相似？ 3 3 55 相似 导入新课 利用刻度尺和量角器画 △ABC和 △A′B′C′，使 ∠A=∠A′， 量出 BC 及 B′C′ 的长， 它们的比值等于 k 吗？再量一量两个三角形另外的 两个角，你有什么发现？△ABC 与 △A′B′C′ 有何关 系？ AB AC k.A' B' A' C'   合作探究 两个三角形相似 改变 k 和∠A 的值的大小，是否有同样的结论？ 讲授新课 两边成比例且夹角相等的两个三角形相似知识点 如图，在△ABC与△A′B′C′中，已知∠A= ∠A′， AB AC .A' B' A' C'  证明： 在 △A′B′C′ 的边 A′B′ 上截取点D， 使 A′D = AB．过点 D 作 DE∥B′C′， 交 A′C′ 于点 E. ∵ DE∥B′C′， ∴ △A′DE∽△A′B′C′. 求证：△ABC∽△A′B′C′. B A C D E B' A' C' A' D A' E .A' B' A' C' ∴ ∴ A′E = AC . 又 ∠A′ = ∠A. ∴ △A′DE ≌ △ABC， ∴ △A′B′C′ ∽ △ABC. B A C D E B' A' C' ∵ A′D=AB， AB AC A' B' A' C'  ， =A' D A' E AC A' B' A' C' A' C'  ，∴ 由此得到利用两边和夹角来判定三角形相似的定理： 两边成比例，且夹角相等的两个三角形相似． 符号语言： ∵ ∠A=∠A′，AB AC A' B' A' C'  ， B A C B' A' C' ∴ △ABC ∽ △A′B′C′ . 归纳： 对于△ABC和 △A′B′C′，如果 A′B′ : AB= A′C′ : AC. ∠B= ∠B′，这两个三角形一定会相似吗？ 不会，如下图，因为不能证明构造的三角形和原三角 形全等. A B C 思考： A′ B′ B″ C′ 结论： 如果两个三角形两边对应成比例，但相等的角 不是两条对应边的夹角，那么两个三角形不一定相 似，相等的角一定要是两条对应边的夹角. 典例精析 例1 根据下列条件，判断 △ABC 和 △A′B′C′ 是否相 似，并说明理由： ∠A=120°，AB=7 cm，AC=14 cm， ∠A′=120°，A′B′=3 cm ，A′C′=6 cm． 解：∵ 7 3 AB A' B'  ， 14 7 6 3 AC A'C'  = ， AB AC .A' B' A' C' ∴ 又 ∠A′ = ∠A，∴ △ABC ∽ △A′B′C′. 1. 在 △ABC 和 △DEF 中，∠C =∠F=70°，AC = 3.5 cm，BC = 2.5 cm，DF =2.1 cm，EF =1.5 cm. 求证：△DEF∽△ABC. A C B F ED 证明： ∵ AC = 3.5 cm，BC = 2.5 cm， DF = 2.1 cm，EF = 1.5 cm， 又 ∵∠C =∠F = 70°，∴ △DEF ∽△ABC. 练一练 3 5 DF EF .AC BC  ∴ 2. 如图，△ABC 与 △ADE 都是等腰三角形，AD=AE， AB=AC，∠DAB=∠CAE. 求证：△ABC ∽△ADE. 证明： ∵ △ABC 与 △ADE 是等腰三角形， ∴ AD =AE，AB = AC， AD AE .AB AC ∴ 又 ∵∠DAB = ∠CAE， ∴ ∠DAB +∠BAE = ∠CAE +∠BAE， 即 ∠DAE =∠BAC，∴△ABC ∽ △ADE. A B C D E 解：∵ AE=1.5，AC=2， 例2 如图，D，E分别是 △ABC 的边 AC，AB 上的点， AE=1.5，AC=2，BC=3，且 ，求 DE 的长. A CB E D 3 4 AD AB  3 4 AE AD .AC AB  ∴ 又∵∠EAD=∠CAB， ∴ △ADE ∽△ABC， 3 4 DE AD BC AB   ，∴ 3 9 4 4DE BC . ∴ 提示：解题时要找准对应边. 证明：∵ CD 是边 AB 上的高， ∴ ∠ADC =∠CDB =90°. ∴△ADC ∽△CDB，∴ ∠ACD =∠B， ∴ ∠ACB =∠ACD +∠BCD =∠B +∠BCD = 90°. 例3 如图，在 △ABC 中，CD 是边 AB 上的高， 且 ，求证 ∠ACB=90°． A B C D =AD CD CD BD ∵ AD CD CD BD  ， 方法总结：解题时需注意隐含条件，如垂直关系， 三角形的高等. 1. 判断 (1) 两个等边三角形相似 ( ) (2) 两个直角三角形相似 ( ) (3) 两个等腰直角三角形相似 ( ) (4) 有一个角是50°的两个等腰三角形相似 ( ) × √ √ × 随堂练习 2. 如图，D 是 △ABC 一边 BC 上一点，连接 AD，使 △ABC ∽ △DBA的条件是 ( ) A. AC : BC=AD : BD B. AC : BC=AB : AD C. AB2 = CD · BC D. AB2 = BD · BC D A B CD AB BC BD AB → 3. 如图 △AEB 和 △FEC (填 “相似” 或 “不相似”) . 54 30 36 45 E A F C B 1 2 相似 解析：当 △ADP ∽△ACB 时， AP : AB =AD : AC ，∴ AP : 12 =6 : 8 ， 解得 AP = 9； 当 △ADP ∽△ABC 时， AD : AB =AP : AC ，∴ 6 : 12 = AP : 8 ， 解得 AP = 4. ∴ 当 AP 的长度为 4 或 9 时， △ADP 和 △ABC 相似． 4. 如图，已知 △ABC中，D 为边 AC 上一点，P 为边 AB上一点，AB = 12，AC = 8，AD = 6，当 AP 的长 度为 时，△ADP 和 △ABC 相似. A B C D 4 或 9 P P 5. 如图，在四边形 ABCD 中，已知 ∠B =∠ACD， AB=6，BC=4，AC=5，CD= ，求 AD 的长．  A B C D 解：∵AB=6，BC=4，AC=5，CD= ，  4 5 AB BC .CD AC  ∴ 又∵∠B=∠ACD， ∴ △ABC ∽ △DCA， 4 5 AC BC AD AC  ∴ ， 25 4AD .∴ 6. 如图，∠DAB =∠CAE，且 AB · AD = AE·AC， 求证△ABC ∽△AED. A B C D E 证明：∵ AB · AD = AE·AC， AB AC .AE AD ∴ 又∵ ∠DAB =∠CAE， ∴∠ DAB +∠BAE =∠CAE +∠BAE ， 即∠DAE =∠BAC， ∴ △ABC ∽△AED. 两边成比例， 且夹角相等的 两个三角形相 似 利用两边及夹角判定三角形相似 相似三角形的判定定理的运用 课堂小结