2020九年级数学上册 第二十一章实际问题与一元二次方程 7页

‎21.3实际问题与一元二次方程 第2课时 一、学习目标：‎ ‎1、能根据具体问题中的数量关系，列出一元二次方程，并能根据具体问题的实际意义，检验结果是否合理；‎ ‎2、通过实际问题中的增降情况，会将应用问题转化为数学问题，能够列一元二次方程解有关增降率的问题；‎ ‎3、进一步掌握列方程解应用题的步骤和关键.‎ 二、学习重难点：‎ 重点：列一元二次方程解决增降率问题等 难点：掌握列方程解应用题的步骤和关键 探究案 三、合作探究 复习旧知 用一元二次方程解应用题的一般步骤是什么？‎ 7‎ 活动1：小组合作 问题：两年前生产 1 吨甲种药品的成本是5000元,生产1吨乙种药品的成本是6000元,随着生产技术的进步,现在生产 1吨甲种药品的成本是3000元,生产1吨乙种药品的成本是3600元，哪种药品成本的年平均下降率较大?‎ 解：①设甲种药品成本的年平均下降率为x，则一年后甲种药品成本为 元，两年后甲种药品成本为 元．‎ 依题意，得 解得：x1≈ ，x2≈ 。‎ 根据实际意义，甲种药品成本的年平均下降率约为 。‎ ‎②设乙种药品成本的平均下降率为y．则，‎ 列方程：‎ 解得：‎ 答：两种药品成本的年平均下降率 ．‎ 活动2：探究归纳 经过计算，你能得出什么结论？成本下降额较大的药品，它的下降率一定也较大吗？应怎样全面地比较几个对象的变化状态？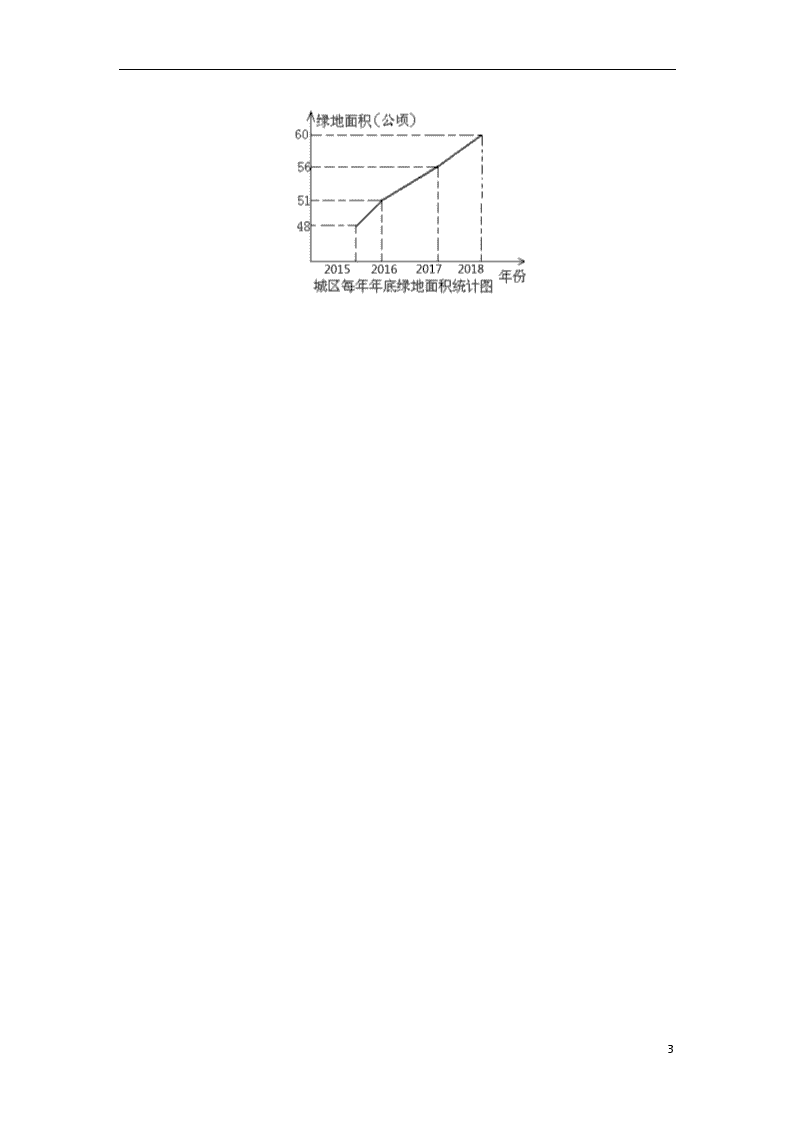‎ 活动内容3：典例精析 例美化城市，改善人们的居住环境已成为城市建设的一项重要内容。某城市近几年来通过拆迁旧房，植草，栽树，修公园等措施，使城区绿地面积不断增加（如图所示）。‎ ‎（1）根据图中所提供的信息回答下列问题：2018年底的绿地面积为__________公顷，比2017年底增加了__________公顷；在2016年，2017年，2018年这三年中，绿地面积增加最多的是__________年；‎ ‎（2）为满足城市发展的需要，计划到2020年底使城区绿地面积达到72.6公顷，试求2019年,2020年两年绿地面积的年平均增长率。‎ 7‎ 7‎ ‎随堂检测 ‎1.某厂今年一月份的总产量为500吨,三月份的总产量为720吨,平均每月增长率是x,列方程( )‎ A.500(1+2x)=720 B.500(1+x)2=720‎ C.500(1+x2)=720 D.720(1+x)2=500‎ ‎2.某校去年对实验器材的投资为2万元,预计今明两年的投资总额为8万元,若设该校今明两年在实验器材投资上的平均增长率是x,则可列方程为___________________________.‎ ‎3. 某银行经过最近的两次降息，使一年期存款的年利率由2.25%降至1.98%，平均每次降息的百分率是多少？‎ ‎4. 雪融超市今年的营业额为280万元，计划后年的营业额为403.2万元，求平均每年增长的百分率？‎ ‎5. ‎2015年4月30日，由中国某民营旅游投资企业斥资3.8亿元，在凤阳山国家级自然保护区内投资开发旅游度假区正式对外开放.到‎2017年4月30日，该企业的投资已经达5.2亿元.求‎2015年4月30日到‎2017年4月30日，该企业投资的年平均增长率（精确到0.1%）.‎ 7‎ ‎6.菜农李伟种植的某蔬菜，计划以每千克5元的价格对外批发销售.由于部分菜农盲目扩大种植，造成该蔬菜滞销，李伟为了加快销售，减少损失，对价格经过两次下调后，以每千克3.2元的价格对外批发销售.‎ ‎（1）求平均每次下调的百分率；‎ ‎（2）小华准备到李伟处购买5吨该蔬菜，因数量多，李伟决定再给予两种优惠方案以供选择：方案一，打九折销售；方案二，不打折，每吨优惠现金200元.试问小华选择哪种方案更优惠？请说明理由.‎ 课堂小结 通过本节课的学习在小组内谈一谈你的收获，并记录下来：‎ 我的收获 ‎__________________________________________________________________________________________________________________________________________________________‎ 7‎ 参考答案 复习旧知 ‎（1）审题，分析题意，找出已知量和未知量，弄清它们之间的数量关系；‎ ‎（2）设未知数，一般采取直接设法，有的要间接设；‎ ‎（3）寻找数量关系，列出方程，要注意方程两边的数量相等，方程两边的代数式的单位相同；‎ ‎（4）选择合适的方法解方程；‎ ‎（5）检验，注意一方面检验结果是不是方程的根，另一方面检验结果是否符合实际意义；‎ ‎（6）作答.‎ 活动1：小组合作 ‎5000(1-x) , 22.5%‎ ‎ , 22.5%‎ 活动2：探究归纳 经过计算,成本下降额较大的药品,它的成本下降率不一定较大,应比较降前及降后的价格.‎ 活动内容3：典例精析 ‎（1）60 4 2017 ‎ ‎（2）解：设2019年,2020年两年绿地面积的年平均增长率为x，‎ 根据题意，得 60 (1＋x)2＝72.6‎ ‎ (1＋x)2=1.21‎ ‎∴1＋x=±1.1‎ ‎∴ x1 = 0.1=10%‎ x2 =－2.1(不合题意,舍去)‎ 答： 2019年,2020年两年绿地面积的年平均增长率为10%．‎ 随堂检测 ‎1.B ‎2. 2（1+x)+2(1+x)2=8‎ ‎3. 解：设平均每次降息的百分率为a%，依题意可列方程为：‎ ‎2.25%（1-a%）²=1.98%‎ 解得a1≈6.19，a2≈193.81（不合题意，舍去）‎ 7‎ 即平均每次降息的百分率约为6.19%.‎ ‎4. 解：设平均每年增长的百分率为x,根据题意，得 ‎1+x=±1.2‎ ‎（舍去），‎ 答：平均每年增长的百分率为20%.‎ ‎5. 设‎2015年4月30‎日至‎2017年4月30日该企业投资的年平均增长率为x，列关系式为:‎ 即 解得： ‎ ‎∵，∴不合题意，舍去.‎ 答：2015年4月30日至2017年4月30日该企业投资的年平均增长率为16.9%. ‎ ‎6.解：（1）设平均每次下调的百分率为x，由题意，得 ‎5(1－x)2=3.2，‎ 解得 x1=20%，x2=1.8 （舍去）‎ ‎∴平均每次下调的百分率为20%;‎ ‎(2)小华选择方案一购买更优惠，理由如下：‎ 方案一所需费用为：3.2×0.9×5000=14400（元）；‎ 方案二所需费用为：3.2×5000－200×5=15000（元），‎ ‎∵14400＜15000，∴小华选择方案一购买更优惠.‎ 7‎