2020年湖南省永州市中考数学试卷【含答案；word版本试题；可编辑】 11页

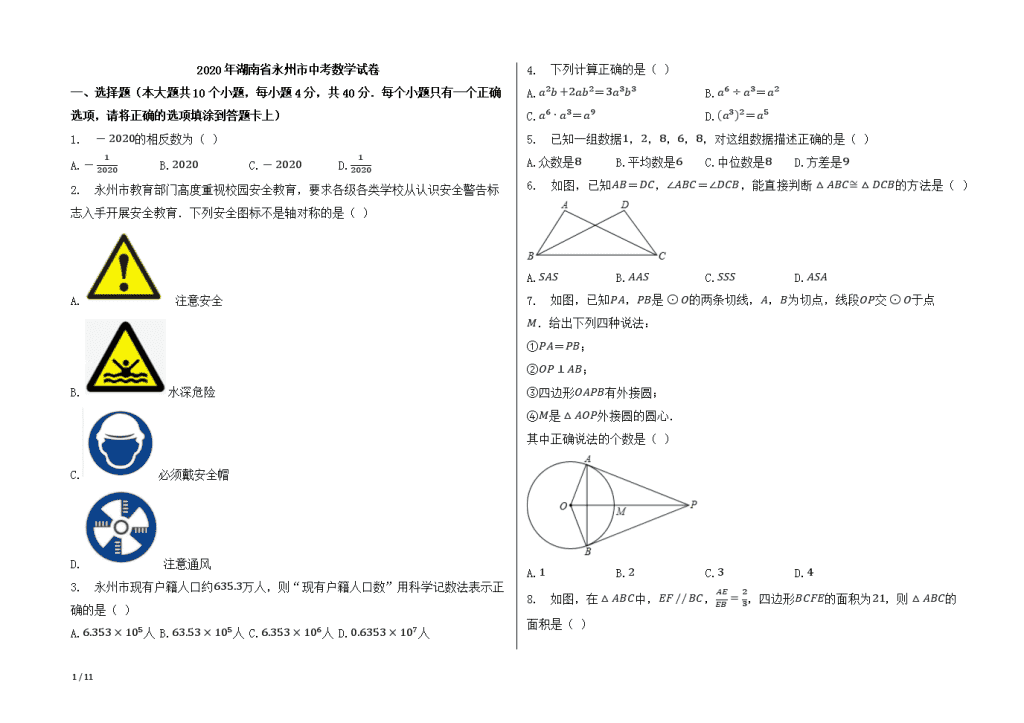
‎2020年湖南省永州市中考数学试卷 一、选择题（本大题共10个小题，每小题4分，共40分．每个小题只有一个正确选项，请将正确的选项填涂到答题卡上）‎ ‎1. ‎-2020‎的相反数为（ ）‎ A.‎-‎‎1‎‎2020‎ B.‎2020‎ C.‎-2020‎ D.‎‎1‎‎2020‎ ‎2. 永州市教育部门高度重视校园安全教育，要求各级各类学校从认识安全警告标志入手开展安全教育．下列安全图标不是轴对称的是（ ）‎ A. 注意安全 B.水深危险 C.必须戴安全帽 D.注意通风 ‎3. 永州市现有户籍人口约‎635.3‎万人，则“现有户籍人口数”用科学记数法表示正确的是（ ）‎ A.‎6.353×‎‎10‎‎5‎人 B.‎63.53×‎‎10‎‎5‎人 C.‎6.353×‎‎10‎‎6‎人 D.‎0.6353×‎‎10‎‎7‎人 ‎4. 下列计算正确的是（ ）‎ A.a‎2‎b+2ab‎2‎＝‎3‎a‎3‎b‎3‎ B.a‎6‎‎÷‎a‎3‎＝‎a‎2‎ C.a‎6‎‎⋅‎a‎3‎＝a‎9‎ D.‎(‎a‎3‎‎)‎‎2‎＝‎a‎5‎ ‎5. 已知一组数据‎1‎，‎2‎，‎8‎，‎6‎，‎8‎，对这组数据描述正确的是（ ）‎ A.众数是‎8‎ B.平均数是‎6‎ C.中位数是‎8‎ D.方差是‎9‎ ‎6. 如图，已知AB＝DC，‎∠ABC＝‎∠DCB，能直接判断‎△ABC≅△DCB的方法是（ ）‎ A.SAS B.AAS C.SSS D.‎ASA ‎7. 如图，已知PA，PB是‎⊙O的两条切线，A，B为切点，线段OP交‎⊙O于点M．给出下列四种说法：‎ ‎①PA＝PB；‎ ‎②OP⊥AB；‎ ‎③四边形OAPB有外接圆；‎ ‎④M是‎△AOP外接圆的圆心．‎ 其中正确说法的个数是（ ）‎ A.‎1‎ B.‎2‎ C.‎3‎ D.‎‎4‎ ‎8. 如图，在‎△ABC中，EF // BC，AEEB‎=‎‎2‎‎3‎，四边形BCFE的面积为‎21‎，则‎△ABC的面积是（ ）‎ ‎ 11 / 11‎ A.‎91‎‎3‎ B.‎25‎ C.‎35‎ D.‎‎63‎ ‎9. 如图，这是一个底面为等边三角形的正三棱柱和它的主视图、俯视图，则它的左视图的面积是（ ）‎ A.‎4‎ B.‎2‎ C.‎3‎ D.‎‎2‎‎3‎ ‎10. 已知点P(x‎0‎, y‎0‎)‎和直线y＝kx+b，求点P到直线y＝kx+b的距离d可用公式d=‎‎|kx‎0‎-y‎0‎+b|‎‎1+‎k‎2‎计算．根据以上材料解决下面问题：如图，‎⊙C的圆心C的坐标为‎(1, 1)‎，半径为‎1‎，直线l的表达式为y＝‎-2x+6‎，P是直线l上的动点，Q是‎⊙C上的动点，则PQ的最小值是（ ）‎ A.‎3‎‎5‎‎5‎ B.‎3‎‎5‎‎5‎‎-1‎ C.‎6‎‎5‎‎5‎‎-1‎ D.‎‎2‎ 二、填空题（本大题共8个小题，每小题4分，共32分．请将答案填在答题卡的答案栏内）‎ ‎11. 函数y=‎‎1‎x-3‎中，自变量x的取值范围是________．‎ ‎12. 方程组x+y=4‎‎2x-y=2‎‎ ‎的解是________．‎ ‎13. 若关于x的一元二次方程x‎2‎‎-4x-m=0‎有两个不相等的实数根，则实数m的取值范围是________．‎ ‎14. 永州市教育部门为了了解全市中小学安全教育情况，对某校进行了“防溺水”安全知识的测试．从七年级随机抽取了‎50‎名学生的测试成绩（百分制），整理样本数据，得到下表：‎ 成绩 ‎90≤x≤100‎ ‎80≤x<90‎ ‎70≤x<80‎ ‎60≤x<70‎ x<60‎ 人数 ‎25‎ ‎15‎ ‎5‎ ‎4‎ ‎1‎ 根据抽样调查结果，估计该校七年级‎600‎名学生中，‎80‎分（含‎8‎以上的学生有________人．‎ ‎15. 已知圆锥的底面周长是π‎2‎分米，母线长为‎1‎分米，则圆锥的侧面积是________平方分米．‎ ‎16. 已知直线a // b，用一块含‎30‎‎∘‎角的直角三角板按图中所示的方式放置，若‎∠1‎＝‎25‎‎∘‎，则‎∠2‎＝________．‎ ‎17. 如图，正比例函数y＝‎-x与反比例函数y=-‎‎6‎x的图象交于A，C两点，过点A作AB⊥x轴于点B，过点C作CD⊥x轴于点D，则‎△ABD的面积为________．‎ ‎ 11 / 11‎ ‎18. ‎∠AOB在平面直角坐标系中的位置如图所示，且‎∠AOB＝‎60‎‎∘‎，在‎∠AOB内有一点P(4, 3)‎，M，N分别是OA，OB边上的动点，连接PM，PN，MN，则‎△PMN周长的最小值是________．‎ 三、解答题（本大题共8个小题，共78分．解答应写出必要的文字说明、证明过程或演算步骤）‎ ‎19. 计算：‎2020‎‎0‎‎+‎3‎‎8‎sin‎30‎‎∘‎-(‎‎1‎‎2‎‎)‎‎-1‎．‎ ‎20. 先化简，再求值：‎(‎1‎a+1‎-a+2‎a‎2‎‎-1‎⋅a‎2‎‎-2a+1‎a‎2‎‎+4a+4‎)⋅(a+2)‎，其中a＝‎2‎．‎ ‎21. 今年‎6‎月份，永州市某中学开展“六城同创”知识竞赛活动．赛后，随机抽取了部分参赛学生的成绩，按得分划为A，B，C，D四个等级，A:90-4‎ ‎14.‎‎480‎ ‎15.‎π‎4‎ ‎16.‎‎35‎‎∘‎ ‎17.‎‎6‎ ‎18.‎‎5‎‎3‎ 三、解答题（本大题共8个小题，共78分．解答应写出必要的文字说明、证明过程或演算步骤）‎ ‎19.原式＝‎‎1+2×‎1‎‎2‎-2‎ ‎＝‎‎1+1-2‎ ‎＝‎0‎．‎ ‎20.原式＝‎[‎1‎a+1‎-a+2‎‎(a+1)(a-1)‎⋅‎(a-1‎‎)‎‎2‎‎(a+2‎‎)‎‎2‎]‎•‎‎(a+2)‎ ‎＝‎[‎1‎a+1‎-a-1‎‎(a+1)(a+2)‎]‎•‎‎(a+2)‎ ‎=a+2‎a+1‎-‎a-1‎a+1‎ ‎=‎‎3‎a+1‎‎，‎ 当a＝‎2‎时，‎ 原式‎=‎3‎‎2+1‎=1‎．‎ ‎21.∵ 被调查的总人数为‎4÷10%‎＝‎40‎（人），‎ ‎∴ C等级人数为‎40-(4+28+2)‎＝‎6‎（人），‎ 补全图形如下：‎ ‎15‎‎,‎5‎,‎‎252‎‎∘‎ 画树状图如下：‎ ‎ 11 / 11‎ 共有‎12‎种可能的结果，恰好抽到‎1‎名男生和‎1‎名女生的有‎8‎种结果，‎ ‎∴ 恰好抽到‎1‎名男生和‎1‎名女生的概率为‎8‎‎12‎‎=‎‎2‎‎3‎．‎ ‎22.这艘渔船在航行过程中没有触礁的危险，理由如下：‎ 作AD⊥BC于D，如图：‎ 则‎∠ADB＝‎∠ADC＝‎90‎‎∘‎，‎ 由题意得：AB＝‎60‎，‎∠BAD＝‎90‎‎∘‎‎-‎‎60‎‎∘‎＝‎30‎‎∘‎，‎ ‎∴ BD=‎1‎‎2‎AB＝‎30‎，AD=‎3‎BD＝‎30‎3‎≈51.9>50‎，‎ ‎∴ 这艘渔船在航行过程中没有触礁的危险；‎ 由（1）得：BD＝‎30‎，AD＝‎30‎‎3‎，‎ ‎∵ BC＝‎3×30‎＝‎90‎，‎ ‎∴ DC＝BC-BD＝‎90-30‎＝‎60‎，‎ 在Rt△ADC中，AC=AD‎2‎+DC‎2‎=‎(30‎3‎‎)‎‎2‎+‎‎60‎‎2‎=30‎7‎≈79.50‎（海里）；‎ 答：A，C之间的距离约为‎79.50‎海里．‎ ‎23.设一次性医用外科口罩的单价是x元，则N95‎口罩的单价是‎(x+10)‎元，依题意有 ‎1600‎x‎=‎‎9600‎x+10‎‎，‎ 解得x＝‎2‎，‎ 经检验，x＝‎2‎是原方程的解，‎ x+10‎‎＝‎2+10‎＝‎12‎．‎ 故一次性医用外科口罩的单价是‎2‎元，N95‎口罩的单价是‎12‎元；‎ 设购进一次性医用外科口罩y只，依题意有 ‎2y+12(2000-y)≤10000‎‎，‎ 解得y≥1400‎．‎ 故至少购进一次性医用外科口罩‎1400‎只．‎ ‎24.如图，连接OC，‎ ‎∵ OB＝OC，‎ ‎∴ ‎∠OBC＝‎∠OCB，‎ ‎∵ AB是直径，‎ ‎∴ ‎∠ACB＝‎90‎‎∘‎，‎ ‎∵ E为BD的中点，‎ ‎∴ BE＝CE＝DE，‎ ‎∴ ‎∠ECB＝‎∠EBC，‎ ‎∵ BD与‎⊙O相切于点B，‎ ‎∴ ‎∠ABD＝‎90‎‎∘‎，‎ ‎∴ ‎∠OBC+∠EBC＝‎90‎‎∘‎，‎ ‎∴ ‎∠OCB+∠ECB＝‎90‎‎∘‎，‎ ‎∴ ‎∠OCE＝‎‎90‎‎∘‎ ‎∴ OC⊥CE，‎ 又∵ OC为半径，‎ ‎∴ CE是‎⊙O的切线；‎ ‎ 11 / 11‎ 连接OE，‎ ‎∵ ‎∠D＝‎∠D，‎∠BCD＝‎∠ABD，‎ ‎∴ ‎△BCD∽△ABD，‎ ‎∴ BDAD‎=‎CDBD，‎ ‎∴ BD‎2‎＝AD⋅CD，‎ ‎∴ ‎(3‎‎5‎‎)‎‎2‎＝‎5AD，‎ ‎∴ AD＝‎9‎，‎ ‎∵ E为BD的中点，AO＝BO，‎ ‎∴ OE=‎1‎‎2‎AD=‎‎9‎‎2‎，‎ ‎∴ O，E两点之间的距离为‎9‎‎2‎．‎ ‎25.设抛物线的解析式为y＝ax‎2‎+bx+c(a≠0)‎，‎ 在等腰Rt△ABC中，OC垂直平分AB，且AB＝‎4‎，‎ ‎∴ OA＝OB＝OC＝‎2‎，‎ ‎∴ A(-2, 0)‎，B(2, 0)‎，C(0, -2)‎，‎ ‎∴ ‎4a+2b+c=0‎‎4a-2b+c=0‎c=-2‎‎ ‎，‎ 解得，a=‎‎1‎‎2‎b=0‎c=-2‎‎ ‎，‎ ‎∴ 抛物线的解析式为y=‎1‎‎2‎x‎2‎-2‎；‎ ‎①设直线l的解析式为y＝kx，M(x‎1‎, y‎1‎)‎，N(x‎2‎, y‎2‎)‎，‎ 由y=‎1‎‎2‎x‎2‎-2‎y=kx‎ ‎，可得‎1‎‎2‎x‎2‎‎-kx-2=0‎，‎ ‎∴ x‎1‎‎+‎x‎2‎＝‎2k，x‎1‎‎⋅‎x‎2‎＝‎-4‎，‎ ‎∴ ‎(x‎1‎-x‎2‎‎)‎‎2‎=(x‎1‎+x‎2‎‎)‎‎2‎-4x‎1‎x‎2‎=4k‎2‎+16‎，‎ ‎∴ ‎|x‎1‎-x‎2‎|=2‎k‎2‎‎+4‎，‎ ‎∴ S‎△CMN‎=‎1‎‎2‎OC⋅|x‎1‎-x‎2‎|=2‎k‎2‎‎+4‎，‎ ‎∴ 当k＝‎0‎时‎2‎k‎2‎‎+4‎取最小值为‎4‎．‎ ‎∴ ‎△CMN面积的最小值为‎4‎．‎ ‎②假设抛物线上存在点P(m, ‎1‎‎2‎m‎2‎-2)‎，使得点P与点Q关于直线l对称，‎ ‎∴ OP＝OQ，即‎1‎‎2‎‎+(‎‎3‎‎2‎‎)‎‎2‎‎=‎m‎2‎‎+(‎1‎‎2‎m‎2‎-2‎‎)‎‎2‎，‎ 解得，m‎1‎‎=‎‎3‎，m‎2‎‎=-‎‎3‎，m‎3‎＝‎1‎，m‎4‎＝‎-1‎，‎ ‎∵ m‎3‎＝‎1‎，m‎4‎＝‎-1‎不合题意，舍去，‎ 当m‎1‎‎=‎‎3‎时，点P(‎3‎,-‎1‎‎2‎)‎，‎ 线段PQ的中点为‎(‎1+‎‎3‎‎2‎,-1)‎，‎ ‎∴ ‎1+‎‎3‎‎2‎k=-1‎，‎ ‎∴ k=1-‎‎3‎，‎ ‎∴ 直线l的表达式为：y＝‎(1-‎3‎)x，‎ 当m‎2‎‎=-‎‎3‎时，点P(-‎3‎, -‎1‎‎2‎)‎，‎ 线段PQ的中点为‎(‎1-‎‎3‎‎2‎, -1)‎，‎ ‎ 11 / 11‎ ‎∴ ‎1-‎‎3‎‎2‎k=-1‎，‎ ‎∴ k=1+‎‎3‎，‎ ‎∴ 直线l的解析式为y＝‎(1+‎3‎)x．‎ 综上，点P(‎3‎, -‎1‎‎2‎)‎，直线l的解析式为y＝‎(1-‎3‎)x或点P(-‎3‎, -‎1‎‎2‎)‎，直线l的解析式为y＝‎(1+‎3‎)x．‎ ‎26.在平移过程中，重叠部分的形状分别为：三角形，梯形，菱形，五边形．如下图所示，‎ 分别过B，D作BE⊥CD于点E，DF⊥CB于点F，如图，‎ ‎∴ ‎∠BEC＝‎∠DFC＝‎90‎‎∘‎，‎ ‎∵ 两纸条等宽，‎ ‎∴ BE＝DF＝‎6‎，‎ ‎∵ ‎∠BCE＝‎∠DCF＝‎45‎‎∘‎，‎ ‎∴ BC＝CD＝‎6‎‎2‎，‎ ‎∵ 两纸条都是矩形，‎ ‎∴ AB // CD，BC // AD，‎ ‎∴ 四边形ABCD是平行四边形，‎ 又BC＝DC，‎ ‎∴ 四边形ABCD是菱形；‎ ‎①当‎0