2009年湖北省黄石市中考数学试题（含答案） 9页

黄石市 2009 年初中毕业生学业考试 数 学 试 题 卷 （2009 年黄石市） 1． 1 2  的倒数是（ ） A． 2 B． 1 2 C． 1 2  D． 2 2．实数 a 在数轴上对应的点如图所示，则 a ， a ， 1 的大小关系是（ ） A． 1a a    B． a a a    C． 1a a    D． 1a a    3．下列根式中，不是．．最简二次根式的是（ ） A． 7 B． 3 C． 1 2 D． 2 4．下列图形中，对称轴有且只有 3 条的是（ ） A．菱形 B．等边三角形 C．正方形 D．圆 5．一次函数 y kx b  的图象只经过第一、二、三象限，则（ ） A． 0 0k b ， B． 0 0k b ， C． 0 0k b ， D． 0 0k b ， 6．一个几何体的三视图如图所示，则此几何体是（ ） A．圆锥 B．棱柱 C．圆柱 D．棱台 7．三角形两边的长是 3 和 4，第三边的长是方程 2 12 35 0x x   的根，则该三角形的周 长为（ ） A．14 B．12 C．12 或 14 D．以上都不对 8．为了防控输入性甲型 H1N1 流感，某市医院成立隔离治疗发热流涕病人防控小组，决定 从内科 5 位骨干医师中（含有甲）抽调 3 人组成，则甲一定抽调到防控小组的概率是（ ） A． 3 5 B． 2 5 C． 4 5 D． 1 5 9．如图， ABC△ 为 O⊙ 的内接三角形， 1 30AB C  ， °，则 O⊙ 的内 接正方形的面积为（ ） A．2 B．4 C．8 D．16 10．已知二次函数 2y ax bx c   的图象如图所示，有以下结论： ① 0a b c   ；② 1a b c   ；③ 0abc  ；④ 4 2 0a b c   ； ⑤ 1c a  其中所有正确结论的序号是（ ） A．①② B． ①③④ C．①②③⑤ D．①②③④⑤ 二、认真填一填（本题有 6 个小题，每小题 3 分，共 18 分） a 1 0 （第 2 题图） （第 6 题图） 俯视图 主视图 左视图 O BA C （第 9 题图） 1 1 1 （第 10 题图） O x y 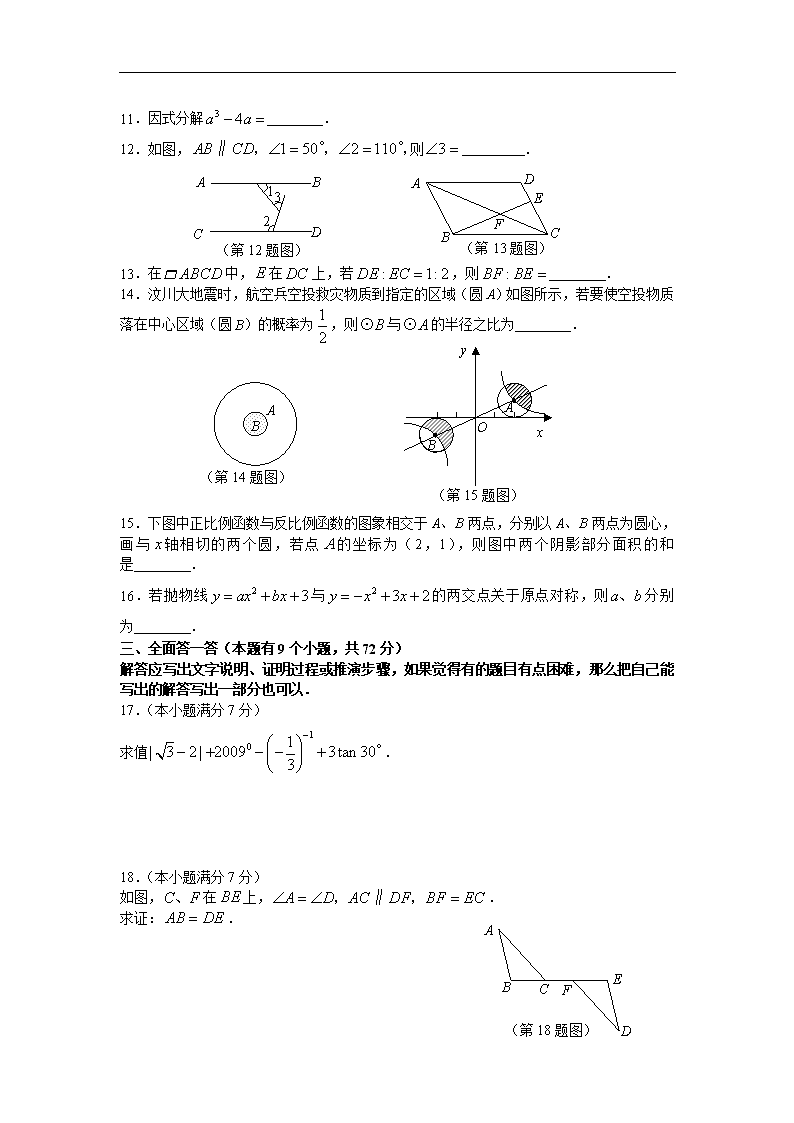11．因式分解 3 4a a  ． 12．如图， 1 50 2 110AB CD    ∥ ， °， °，则 3  ． 13．在 ABCD 中， E 在 DC 上，若 : 1: 2DE EC  ，则 :BF BE  ． 14．汶川大地震时，航空兵空投救灾物质到指定的区域（圆 A）如图所示，若要使空投物质 落在中心区域（圆 B）的概率为 1 2 ，则 B⊙ 与 A⊙ 的半径之比为 ． 15．下图中正比例函数与反比例函数的图象相交于 A B、 两点，分别以 A B、 两点为圆心， 画与 x 轴相切的两个圆，若点 A 的坐标为（2，1），则图中两个阴影部分面积的和是 ． 16．若抛物线 2 3y ax bx   与 2 3 2y x x    的两交点关于原点对称，则 a b、 分别 为 ． 三、全面答一答（本题有 9 个小题，共 72 分） 解答应写出文字说明、证明过程或推演步骤，如果觉得有的题目有点困难，那么把自己能 写出的解答写出一部分也可以． 17．（本小题满分 7 分） 求值 1 0 1| 3 2 | 2009 3tan303         °． 18．（本小题满分 7 分） 如图，C F、 在 BE 上， A D AC DF BF EC   ， ∥ ， ． 求证： AB DE ． A B DC （第 12 题图） 1 2 3 D C A B F E （第 13 题图） A B （第 14 题图） A x y O B （第 15 题图） A B C F E D（第 18 题图） 19．（本小题满分 7 分） 先化简，再求值 2 2 2 36 6 5 10 25 2 10 6 a a a a a a a a       其中 2 2a  ． 20．（本小题满分 8 分）已知关于 x 的函数 2 1y ax x   （ a 为常数） （1）若函数的图象与 x 轴恰有一个交点，求 a 的值；（4 分） （2）若函数的图象是抛物线，且顶点始终在 x 轴上方，求 a 的取值范围．（4 分） 21．（本小题满分 8 分） 三楚第一山——东方山是黄石地区的佛教圣地，也是国家 AAA 级游览景区．它的主峰海拔 约为 600 米，主峰 AB 上建有一座电信信号发射架 BC ，现在山脚 P 处测得峰顶的仰角为 ， 发射架顶端的仰角为  ，其中 3 5tan tan5 8   ， ，求发射架高 BC ． 22．（本小题满分 8 分） 全国实施“限塑令”于今年 6 月 1 日满一年，某报三名记者当日分别在武汉三大商业集团门 口，同时采用问卷调查的方式，随机调查了一定数量的顾客，在“限塑令”实施前后使用购 物袋的情况．下面是这三名记者根据汇总的数据绘制的统计图． C B AP   （第 21 题图） 600 米 山顶 发射架 0 1 2 3 4 5 6 图 1 人数(人) 塑料袋数(个) “限塑令”实施前，平均一次购物使用 不同数量塑料购物袋的人数统计图 押金式 环保袋 24% 其它 4% 收 费 塑 料 购 物 袋 % 自备袋 46% 1% “限塑令”实施后，使用各种购物袋 的人数分布统计图 图 2 橡塑袋 请你根据以上信息解答下列问题 （1）图 1 中从左到右各长方形的高度之比为 2∶8∶8∶3∶3∶1，又知此次调查中使用 4 个 和 5 个塑料购物袋的顾客一共 24 人，问这三名记者一共调查了多少人？（2 分） （2）“限塑令”实施前，如果每天约有 6000 人到该三大商场购物，根据记者所调查的一定 数量顾客平均一次购物使用塑料购物袋的平均数，估计这三大商业集团每天需要为顾客提供 多少个塑料购物袋？（3 分） （3）据武汉晚报报道，自去年 6 月 1 日到去年 12 月底，三大商业集团下属所有门店，塑料 袋的使用量与上一年同期相比，从 12927 万个下降到 3355 万个，降幅为 （精确 到百分之一）．这一结果与图 2 中的收费塑料购物袋 %比较，你能得出什么结论， 谈谈你的感想．（3 分） 23．（本小题满分 8 分） 为了扩大内需，让惠于农民，丰富农民的业余生活，鼓励送彩电下乡，国家决定对购买彩电 的农户实行政府补贴．规定每购买一台彩电，政府补贴若干元，经调查某商场销售彩电台数 y （台）与补贴款额 x（元）之间大致满足如图①所示的一次函数关系．随着补贴款额 x 的 不断增大，销售量也不断增加，但每台彩电的收益 Z （元）会相应降低且 Z 与 x 之间也大 致满足如图②所示的一次函数关系． （1）在政府未出台补贴措施前，该商场销售彩电的总收益额为多少元？（2 分） （2）在政府补贴政策实施后，分别求出该商场销售彩电台数 y 和每台家电的收益 Z 与政府 补贴款额 x 之间的函数关系式；（3 分） （3）要使该商场销售彩电的总收益 w （元）最大，政府应将每台补贴款额 x 定为多少？并 求出总收益 w 的最大值．（3 分） 24．（本小题满分 9 分） 如图， ABC△ 中，点O 是边 AC 上一个动点，过O 作直线 MN BC∥ ，设 MN 交 BCA 的平分线于点 E ，交 BCA 的外角平分线于点 F ． （1）探究：线段OE 与OF 的数量关系并加以证明；（3 分） 1200 800 0 400 y(台) x(元) z(元) x(元) 200 160 2000 图① 图② （2）当点O 在边 AC 上运动时，四边形 BCFE 会是菱形吗？若是，请证明，若不是，则说 明理由；（3 分） （3）当点 O 运动到何处，且 ABC△ 满足什么条件时，四边形 AECF 是正方形？（3 分） 25．（本小题满分 10 分） 正方形 ABCD 在如图所示的平面直角坐标系中，A 在 x 轴正半轴上，D 在 y 轴的负半轴上， AB 交 y 轴正半轴于 E BC， 交 x 轴负半轴于 F ， 1OE  ，抛物线 2 4y ax bx   过 A D F、 、 三点． （1）求抛物线的解析式；（3 分） （2）Q 是抛物线上 D F、 间的一点，过Q 点作平行于 x 轴的直线交边 AD 于 M ，交 BC 所 在直线于 N ，若 3 2 FQNAFQMS S △四边形 ，则判断四边形 AFQM 的形状；（3 分） （3）在射线 DB 上是否存在动点 P ，在射线 CB 上是否存在动点 H ，使得 AP PH⊥ 且 AP PH ，若存在，请给予严格证明，若不存在，请说明理由．（4 分） 黄石市 2009 年初中毕业生学业考试 数学答案及评分标准 一、选择题（每小题 3 分，共 30 分） 题号 1 2 3 4 5 6 7 8 9 10 答案 D C C B B C B A A C 二、填空题（每小题 3 分，共 18 分） 11． ( 2)( 2)a a a  12．60° 13．3∶5 14． 2 2 15．π 16． 3 32  ， A F N DCB M E O （第 24 题图） （第 25 题图） O y x B E A D C F 三、解答题（9 小题，共 72 分） 17．解：原式 32 3 1 3 3 3       ··································································4 分 6 ···························································································3 分 18．证明： AC DF ∥ ， ACE DFB   ，  ACB DFE   ．···············································2 分 又 BF EC ， BF CF EC CF    ，即 BC EF ．·····················2 分 又 A D   ， ABC DEF△ ≌△ ． AB DE  ．································································································ 3 分 19．解：原式 2 (6 )(6 ) 2( 5) 5 ( 5) 6 ( 6) a a a a a a a a         ·················································· 4 分 2 a  ．······················································································· 2 分 当 2 2a  时，原式 2 2  ．·············································································1 分 20．解：（1）当 0a  时，函数为 1y x  ，它的图象显然与 x 轴 只有一个交点 ( 1 0) ， ．····················································································· 2 分 当 0a  时，依题意得方程 2 1 0ax x   有两等实数根． 1 4 0a    ， 1 4a  ． 当 0a  或 1 4a  时函数图象与 x 轴恰有一个交点．············································ 2 分 （2）依题意有 4 1 04 a a   分类讨论解得 1 4a  或 0a  ． 当 1 4a  或 0a  时，抛物线顶点始终在 x 轴上方．················································4 分 21．解：在 Rt PAB△ 中， ∵ tan AB PA   ， ∴ 600 1000m3tan 5 ABPA    ．··················· 3 分 在 Rt PAC△ 中， ∵ tan AC PA   ， C B AP   600m A B C F E D ∴ 5tan 1000 625m8AC PA     ．·······························································3 分 ∴ 625 600 25mBC    ．············································································· 2 分 答：发射架高为 25m． 22．解：（1）设一次购物用 6 个袋的人数为 x 人，则依条件有 3 3 24 4x x x   ，则记者共调查了 4(2 8 8 3 3 1) 100      人．················· 2 分 （2）这 100 位顾客平均一次购物使用购物袋的平均数为 8 1 32 2 32 3 12 4 12 5 4 6 3100             （个） 6000 3 18000  个． 估计这三大商业集团为顾客每天提供 18000 个塑料购物袋．·····································3 分 （3）74%；25； 多数人环保意识增强，（只要是涉及环保节能等方面思想向上的即可）．······················3 分 23．解：（1）该商场销售家电的总收益为800 200 160000  （元）························ 2 分 （2）依题意可设 1 800y k x  ， 2 200Z k x  有 1400 800 1200k   ， 2200 200 160k   ， 解得 1 2 11 5k k  ， ． 所以 800y x  ， 1 2005Z x   ．································································· 3 分 （3） 1( 800) 2005W yZ x x        21 ( 100) 1620005 x    政府应将每台补贴款额 x 定为 100 元，总收益有最大值． 其最大值为162000元．····················································································3 分 24．解：（1）OE OF ． 其证明如下： ∵CE 是 ACB 的平分线， 1 2   ． ∵ MN BC∥ ，∴ 1 3   ． ∴ 2 3   ． ∴OE OC ． 同理可证OC OF ． ∴OE OF ．················································3 分 （2）四边形 BCFE 不可能是菱形，若 BCFE 为菱形，则 BF EC⊥ ，而由（1）可知 FC EC⊥ ，在平面内过同一点 F 不可能有两条直线同垂直于一条直线．·················· 3 分 （3）当点 O 运动到 AC 中点时， OE OF ， OA OC ，则四边形 AECF 为 ，要使 AECF 为正方形，必须使 EF AC⊥ ． ∵ EF BC∥ ，∴ AC BC⊥ ，∴ ABC△ 是以 ACB 为直角的直角三角形， A F N DCB M E O （第 24 题图） 1 2 5 4 3 6 ∴当点 O 为 AC 中点且 ABC△ 是以 ACB 为直角的直角三角形时， 四边形 AECF 是正方形．················································································· 3 分 25．解：（1）依条件有 (0 4)D ， ， (01)E ， ． 由 OEA ADO△ ∽△ 知 2 4OA OE OD  ． ∴ (2 0)A ， 由 Rt RtADE ABF△ ≌ △ 得 DE AF ． ∴ ( 3 0)F  ， ． 将 A F、 的坐标代入抛物线方程， 得 4 2 4 0 9 3 4 0 a b a b        2 3a b   ． ∴抛物线的解析式为 22 2 43 3y x x   ．·····························································3 分 （2）设QM m ， 1 ( 5) | |2 QAFQMS m y  四边形 ， 1 (5 ) | |2FQN QS m y  △ ． ∴ 3( 5) | | (5 ) | | 12Q Qm y m y m      设 ( )Q a b， ，则 ( 1 )M a b ， ∴ 22 2 43 2( 1) 4 b a aa b a         2 2 3 0a a    ， 1a   （舍去 3a  ） 此时点 M 与点 D 重合，QF AM ， AF QM ， AF QM∥ ， 则 AFQM 为等腰梯形．··················································································· 3 分 （3）在射线 DB 上存在一点 P ，在射线CB 上存在一点 H ． 使得 AP PH⊥ ，且 AP PH 成立，证明如下： 当点 P 如图①所示位置时，不妨设 PA PH ，过点 P 作 PQ BC⊥ ， PM CD⊥ ， PN AD⊥ ，垂足分别为Q M N、 、 ． 若 PA PH ．由 PM PN 得： B A N DMC Q H P ① H N A DC BMP ③ O y x B E A D C F N M Q B A D M C Q H P ② N AN PQ ， Rt RtPQH APN △ ≌ △ HPQ PAN   ． 又 90PAN APN    ° 90APN HPQ    ° AP PH ⊥ ．·······························································································2 分 当点 P 在如图②所示位置时， 过点 P 作 PM BC⊥ ， PN AB⊥ ， 垂足分别为 M N， ． 同理可证 Rt RtPMH PAN△ ≌ △ ． MHP NAP   ． 又 MHP HPN   ， 90HPA NPA HPN MHP HPM          °， PH PA ⊥ ．······························································································· 1 分 当 P 在如图③所示位置时，过点 P 作 PN BH⊥ ，垂足为 N ， PM AB⊥ 延长线，垂足为 M ． 同理可证 Rt RtPHM PMA△ ≌ △ ． PH PA ⊥ ．······························································································· 1 分 注意：分三种情况讨论，作图正确并给出一种情况证明正确的，同理可证出其他两种情况的 给予 4 分；若只给出一种正确证明，其他两种情况未作出说明，可给 2 分，若用四点共圆知 识证明且证明过程正确的也没有讨论三种情况的．只给 2 分．