2019年天津中考数学试题（解析版） 16页

‎{来源}2019年天津中考数学 ‎{适用范围:3． 九年级}‎ ‎{标题}2019年天津市初中毕业生学生考试试卷 数学 试卷满分120分，考试时间100分钟。‎ 第I卷 ‎{题型:1-选择题}一、选择题（本大题12小题，每小题3分，共36分）‎ ‎{题目}1.（2019年天津）计算（-3）×9的结果等于（ ）‎ A. -27 B. -6 C. 27 D. 6‎ ‎{答案}A ‎{解析}本题考查了有理数的乘法，两数相乘，同号得正，异号得负，并把绝对值相乘，故原式=-3×9=-27，因此本题选A．‎ ‎{分值}3‎ ‎{章节:[1-1-4-1]有理数的乘法}‎ ‎{考点:有理数的乘法法则}‎ ‎{类别:常考题}‎ ‎{难度:1-最简单}‎ ‎{题目}2.（2019年天津）的值等于（ ）‎ A. 1 B. C. D. 2‎ ‎【解析】锐角三角函数计算，故选A.‎ ‎{答案}B ‎{解析}本题考查了特殊角的锐角三角形函数，由于，所以=2×=，因此本题选B．‎ ‎{分值}3‎ ‎{章节:[1-28-3]锐角三角函数}‎ ‎{考点:特殊角的三角函数值}‎ ‎{类别:常考题}‎ ‎{难度:1-最简单}‎ ‎{题目}3.（2019年天津）据2019年3月21日《天津日报》报道：“伟大的变革---庆祝改革开放四十周年大型展览”3月20日圆满闭幕，自开幕以来，现场观众累计约为4 230 000人次，将4 230 000用科学记数法表示为（ ）‎ A. 0.423×107 B.4.23×106 C.42.3×105 D.423×104‎ ‎{答案}B ‎{解析}本题考查了科学记数法，将一个数写成a×10n的形式，叫做科学记数法.其中a是整数数位有且仅有一位的数，即a应满足1≤|a|＜10；当原数的绝对值不小于1时，n等于原数的整数位数减去1所得的差；当原数的绝对值小于1时，n等于原数左起第一位非零数字前面所有0的个数的相反数.4 230 000=4.23×106，因此本题选B．‎ 本题考查了，，因此本题选．‎ ‎{分值}3‎ ‎{章节:[1-1-5-2]科学计数法}‎ ‎{考点:将一个绝对值较大的数科学计数法}‎ ‎{类别:常考题}‎ ‎{难度:1-最简单}‎ ‎{题目}4.（2019年天津）在一些美术字中，有的汉字是轴对称图形，下面4个汉字中，可以看作是轴对称图形的是（ ）‎ A. B. C. 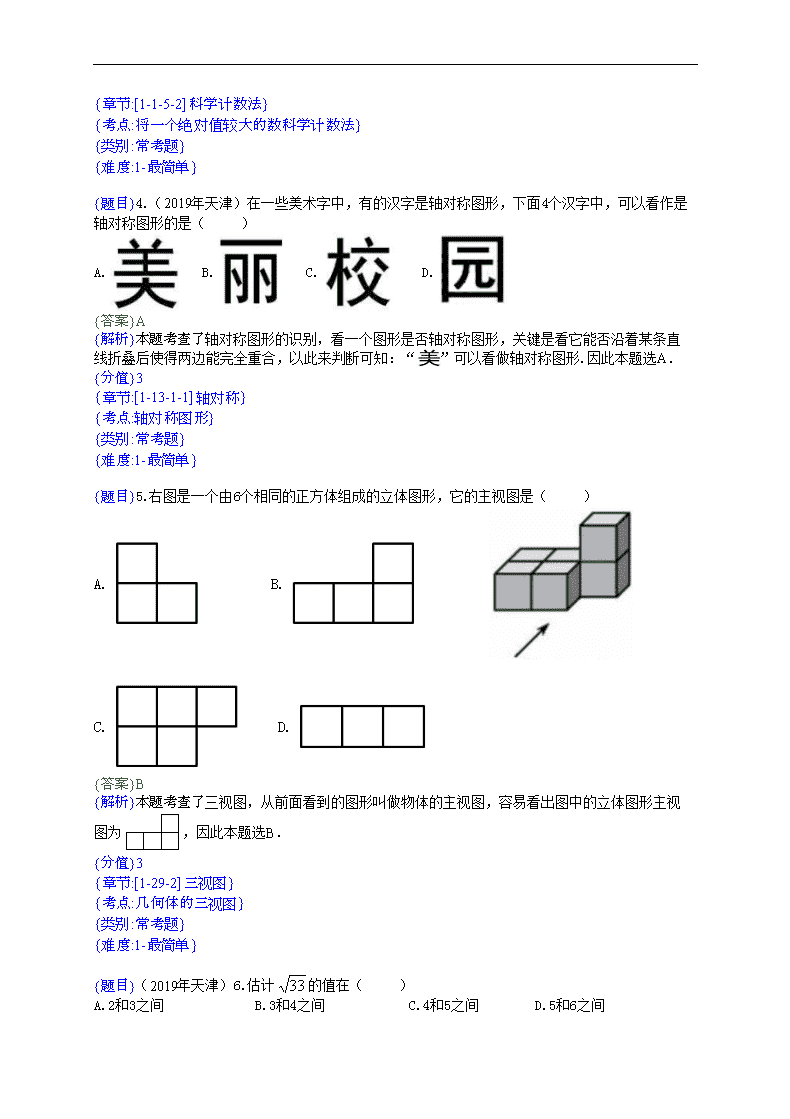D.‎ ‎{答案}A ‎{解析}本题考查了轴对称图形的识别，看一个图形是否轴对称图形，关键是看它能否沿着某条直线折叠后使得两边能完全重合，以此来判断可知：“”可以看做轴对称图形.因此本题选A．‎ ‎{分值}3‎ ‎{章节:[1-13-1-1]轴对称}‎ ‎{考点:轴对称图形}‎ ‎{类别:常考题}‎ ‎{难度:1-最简单}‎ ‎{题目}5.右图是一个由6个相同的正方体组成的立体图形，它的主视图是（ ）‎ A. B. ‎ C. D.‎ ‎{答案}B ‎{解析}本题考查了三视图，从前面看到的图形叫做物体的主视图，容易看出图中的立体图形主视图为，因此本题选B．‎ ‎{分值}3‎ ‎{章节:[1-29-2]三视图}‎ ‎{考点:几何体的三视图}‎ ‎{类别:常考题}‎ ‎{难度:1-最简单}‎ ‎{题目}（2019年天津）6.估计的值在（ ）‎ A.2和3之间 B.3和4之间 C.4和5之间 D.5和6之间 ‎{答案}D ‎{解析}本题考查了算术平方根型的无理数的估算，因为＜＜，所以5＜＜6，因此本题选D．‎ ‎{分值}3‎ ‎{章节:[1-6-3]实数}‎ ‎{考点:无理数的估值}‎ ‎{类别:常考题}‎ ‎{难度:2-简单}‎ ‎{题目}7.（2019年天津）计算的结果是（ ）‎ A. 2 B. C. 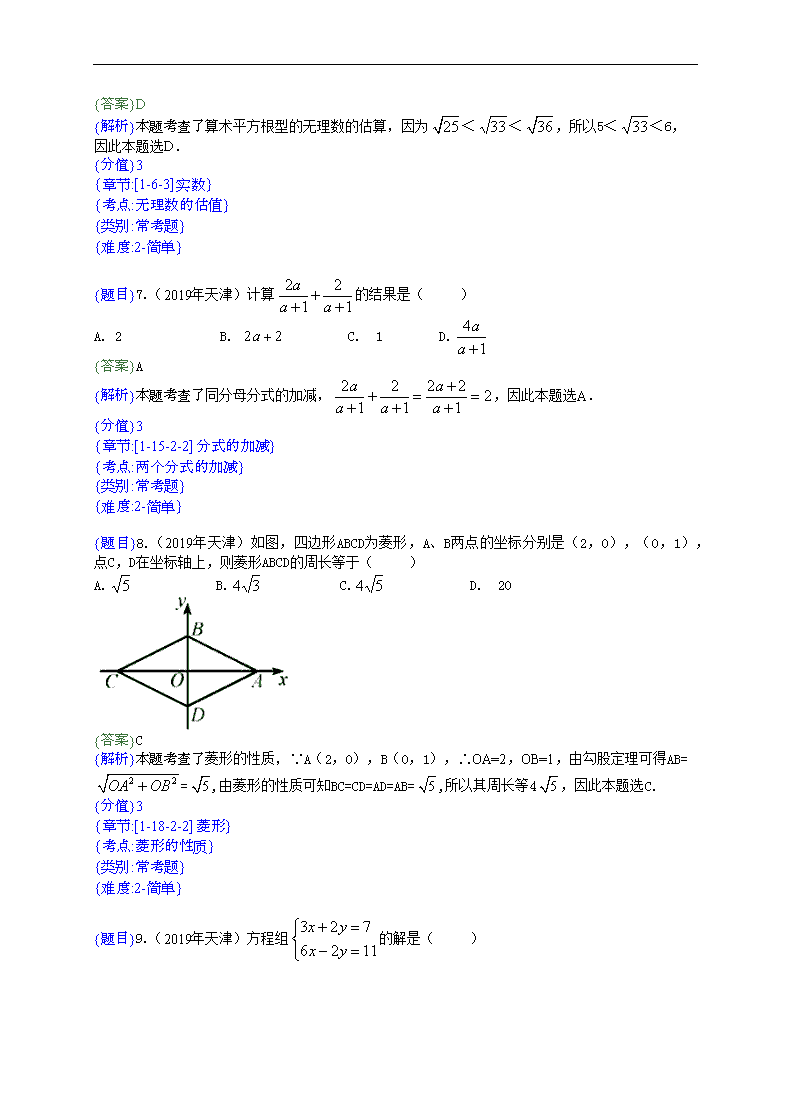1 D.‎ ‎{答案}A ‎{解析}本题考查了同分母分式的加减，，因此本题选A．‎ ‎{分值}3‎ ‎{章节:[1-15-2-2]分式的加减}‎ ‎{考点:两个分式的加减}‎ ‎{类别:常考题}‎ ‎{难度:2-简单}‎ ‎{题目}8.（2019年天津）如图，四边形ABCD为菱形，A、B两点的坐标分别是（2，0），（0，1），点C，D在坐标轴上，则菱形ABCD的周长等于（ ） ‎ A. B. C. D. 20‎ ‎{答案}C ‎{解析}本题考查了菱形的性质，∵A（2，0），B（0，1），∴OA=2，OB=1，由勾股定理可得AB==,由菱形的性质可知BC=CD=AD=AB=,所以其周长等4，因此本题选C.‎ ‎{分值}3‎ ‎{章节:[1-18-2-2]菱形}‎ ‎{考点:菱形的性质}‎ ‎{类别:常考题} ‎ ‎{难度:2-简单} ‎ ‎{题目}9.（2019年天津）方程组的解是（ ）‎ A. B. C. D.‎ ‎{答案}D ‎{解析}本题考查了二元一次方程组的解法，用加减消元法解方程组，①+②，得9x=18，∴x=2， 将x=2代入①得，，解得，从而方程组的解为，因此本题选D.‎ ‎{分值}3‎ ‎{章节:[1-8-2]消元——解二元一次方程组}‎ ‎{考点:加减消元法}‎ ‎{类别:常考题}‎ ‎{难度:2-简单}‎ ‎{题目}10.（2019年天津）若点A（-3，），B（-2，），C（1，）都在反比函数的图象上，则，，的大小关系是（ ）‎ A. B. C. D.‎ ‎{答案}B ‎{解析}本题考查了反比例函数的性质，将（-3，），（-2，），（1，）代入，得：，所以，因此本题选B．‎ ‎{分值}3‎ ‎{章节:[1-26-1]反比例函数的图像和性质}‎ ‎{考点:反比例函数的性质}‎ ‎{类别:常考题}‎ ‎{难度:2-简单} ‎ ‎{题目}11.（2019年天津）如图，将△ABC绕点C顺时针旋转得到△DEC，使点A的对应点D恰好落在边AB上，点B的对应点为E，连接BE，下列结论一定正确的是（ ）‎ A.AC=AD B.AB⊥EB C. BC=DE D.∠A=∠EBC ‎{答案}D ‎{解析}本题考查了图形旋转的性质，由旋转性质可知，AC=CD，AC不一定等于AD，∴A选项错；由旋转性质可知，BC=EC，BC不一定等于DE，∴C错；由旋转性质可知，∠ACB=∠DCE，∠ACD=∠ECB，‎ AC=CD，BC=CE，∴∠A=∠CDA=（180°-∠ECB），∠EBC=∠CEB=（180°-∠ECB），∴∠A=∠‎ EBC，∴D正确；要想∠ABE=90°，需∠ABC+∠EBC=∠ABC+∠A=90°，这就需要∠ACB=90°，而由题意不能得到∠ACB=90°，∴B选项错误.因此本题选D．‎ ‎{分值}3‎ ‎{章节:[1-23-1]图形的旋转}‎ ‎{考点:旋转的性质}‎ ‎{类别:常考题}‎ ‎{难度:3-中等难度} ‎ ‎{题目}12.（2019年天津）二次函数y＝ax2+bx+c（a，b，c是常数，a≠0）的自变量x与函数值y的部分对应值如下表：‎ x ‎…‎ ‎-2‎ ‎-1‎ ‎0‎ ‎1‎ ‎2‎ ‎…‎ y＝ax2+bx+c ‎…‎ t m ‎-2‎ ‎-2‎ n ‎…‎ 且当x=时，与其对应的函数值，有下列结论：‎ ‎①abc＞0；② －2和3是关于x的方程ax2+bx+c＝t的两个根；③0＜m+n＜.其中，正确结论的个数是（ ）‎ A.0 B.1 C. 2 D.3‎ ‎{答案}C ‎{解析}本题考查了二次函数的图象与性质.由表格可知，抛物线y＝ax2+bx+c过点（0，-2），（1，-2），∴c＝﹣2，a+b﹣2＝﹣2，∴a+b＝0，∵a≠0，∴ab＜0，从而可得abc＞0，‎ ‎∴①正确；抛物线为y＝ax2﹣ax﹣2，x‎=‎‎1‎‎2‎是对称轴，x＝﹣2时y＝t，故由抛物线的轴对称性可知当x＝3时，y＝t，∴﹣2和3是关于x的方程ax2+bx+c＝t的两个根，故②正确；将（-1，m）、（2，n）代入解析式y＝ax2﹣ax﹣2得m＝n＝2a﹣2，∴m＝n＝2a﹣2，∴m+n＝4a﹣4，∵当x=时，y＞0，∴，∴a‎＞‎‎8‎‎3‎，∴m+n‎＞‎‎20‎‎3‎，故③错误.因此本题选C．‎ ‎{分值}3‎ ‎{章节:[1-22-1-4]二次函数y=ax2+bx+c的图象和性质}‎ ‎{考点:二次函数y＝ax2+bx+c的性质}‎ ‎{类别:常考题}‎ ‎{难度:4-较高难度}‎ 第II卷 二、填空题（本大题共6小题，每小题3分，共18分）‎ ‎{题目}13.（2019年天津）计算x5•x的结果等于 .‎ ‎{答案}x6‎ ‎{解析}本题考查了同底数幂的乘法，根据“同底数幂相乘，底数不变，指数相加”，可知x5•x＝x6．因此本题答案为：x6．‎ ‎{分值}3‎ ‎{章节:[1-14-1]整式的乘法}‎ ‎{考点:同底数幂的乘法}‎ ‎{类别:常考题}‎ ‎{难度:1-最简单}‎ ‎{题目}14.（2019年天津）计算（）（）的结果等于 .‎ ‎{答案}2‎ ‎{解析}本题考查了二次根式的乘除，由平方差公式得原式＝＝3﹣1＝2．因此本题答案为：2．‎ ‎{分值}3‎ ‎{章节:[1-16-2]二次根式的乘除}‎ ‎{考点:二次根式的乘法法则}‎ ‎{类别:常考题}‎ ‎{难度:2-简单}‎ ‎{题目}15.（2019年天津）不透明袋子中装有7个球，其中有2个红球，3个绿球和2个蓝球，这些球除颜色外无其他差别，从袋子中随机取出1个球，则它是绿球的概率是 .‎ ‎{答案}‎ ‎{解析}本题考查了等可能条件下的概率的计算，因为不透明袋子装有7个球，其中3个绿球，所以从袋子中随机取出一个球，有7种等可能的结果，其中是绿球的有三种，∴P（摸出1个球是绿球）=.因此本题答案为：．‎ ‎{分值}3‎ ‎{章节:[1-25-1-2]概率}‎ ‎{考点:一步事件的概率}‎ ‎{类别:常考题}‎ ‎{难度:1-最简单}‎ ‎{题目}16.（2019年天津）直线与x轴交点坐标为 .‎ ‎{答案}（，0）‎ ‎{解析}本题考查了一次函数图象的性质，求直线与x轴的交点坐标，就要求出当y=0时，x的值为多少.令，得，所以直线与x轴交点坐标为（，0）.因此本题答案为：（，0）．‎ ‎{分值}3‎ ‎{章节:[1-19-2-2]一次函数}‎ ‎{考点:一次函数的性质}‎ ‎{类别:常考题}‎ ‎{难度:2-简单}‎ ‎{题目}17.（2019年天津）如图，正方形纸片ABCD的边长为12，E是边CD上一点，连接AE.折叠该纸片，使点A落在AE上的G点，并使折痕经过点B，得到折痕BF，点F在AD上，若DE=5，则GE的长为 .‎ ‎{解析}本题考查了正方形的性质、勾股定理及折叠的有关性质.设AE、BF交于点H.在正方形ABCD中，AB＝AD＝12，∠BAD＝∠D＝90°，由折叠知，△ABF≌△GBF，BF垂直平分AG，∴BF⊥AE，AH＝GH，∴∠FAH+∠AFH＝90°，又∵∠FAH+∠BAH＝90°，∴∠AFH＝∠BAH，∴△ABF≌△DAE（AAS），∴AF＝DE＝5，由勾股定理得，AE=BF=13，S△ABF‎=‎AB•AF‎=‎BF•AH，∴AB•AF‎=‎BF•AH，∴12×5＝13AH，∴AH‎=‎，∴AG＝2AH‎=‎，∴GE＝AE﹣AG＝13-=.因此本题答案为：．‎ ‎{分值}3‎ ‎{章节:[1-18-2-3] 正方形}‎ ‎{考点:正方形的性质}‎ ‎{类别:常考题}‎ ‎{难度:4-较高难度}‎ ‎{题目}18.（2019年天津）如图，在每个小正方形得边长为1的网格中，△ABC的顶点A在格点上，B是小正方形边的中点，∠ABC=50°，∠BAC=30°，经过点A、B的圆的圆心在边AC上.‎ ‎（1）线段AB的长等于 ；‎ ‎（2）请用无刻度的直尺，在如图所示的网格中，画出一个点P，使其满足∠PAC=∠PBC=∠PCB，并简要说说明点P的位置是如何找到的（不要求证明） .‎ ‎{答案}（1）；（2）利用圆与网格线的交点画出一条直径与AC相交得到圆心O，取AB与网格线的交点F，连接FO并延长交⊙O于点G，连接GC并延长交BO于点P，连接AP，即可找到点P．‎ ‎{解析}本题第（1）问考查了勾股定理，由勾股定理得AB=；第（2）问考查了正方形网格和圆的背景下的网格直尺作图问题，综合性较强.先利用90°的圆周角所对的弦是直径，两条直径的交点为圆心找出圆心.如图，取圆与网格线的交点D，E，连接DE交AC于点O，则点O是圆心.再取AB与网格线的交点F，连接FO并延长交⊙O于点G，连接GC并延长交BO于点P，连接AP，则点P就是满足条件∠PAC＝∠PBC＝∠PCB的点.简要证明如下：根据题意容易知道∠OAF＝∠OBF＝30°，∠AOF＝∠BOF＝∠BOC＝∠GOC＝60°，从而可得∠OBC＝20°，利用“SAS”证明△GOC≌△GBC，得到∠G=∠OBC=20°，从而可求出∠OPG=40°，从而可得∠PCB＝∠OPG-∠PBC＝20°=∠PBC.利用“SAS”证明△GOP≌△AOP，得到∠PAC=∠G=20°，从而可证出∠PAC＝∠PBC＝∠PCB.因此本题答案为：（1）；（2）利用圆与网格线的交点画出一条直径与AC相交得到圆心O，取AB与网格线的交点F，连接FO并延长交⊙O于点G，连接GC并延长交BO于点P，连接AP，即可找到点P．‎ ‎{分值}3‎ ‎{章节:[1-24-1-4]圆周角}‎ ‎{考点:圆周角定理}‎ ‎{考点:直径所对的圆周角}‎ ‎{考点:几何综合}‎ ‎{类别:高度原创}‎ ‎{类别:发现探究}‎ ‎{难度:6-竞赛题}‎ 三、解答题（本大题共7小题，共66分，解答题写出文字说明、演算步骤或推理过程）‎ ‎{题目}19.（2019年天津）（本小题8分）‎ 解不等式请结合题意填空，完成本题的解答：‎ ‎（I）解不等式①，得 ；‎ ‎（II）解不等式②，得 ；‎ ‎（III）把不等式①和②的解集在数轴上表示出来：‎ ‎（IV）原不等式组的解集为 .‎ ‎{解析}本题考查了一元一次不等式组的解法，由于采用了填空的形式，因此考生只需按题中所提供的解题步骤依次完成即可．‎ ‎{答案}（Ⅰ）x≥﹣2；‎ ‎（Ⅱ）x≤1；‎ ‎（Ⅲ）‎ ‎（Ⅳ）﹣2≤x≤1．‎ ‎{分值}8‎ ‎{章节:[1-9-3]一元一次不等式组}‎ ‎{难度:2-简单} ‎ ‎{类别:常考题}‎ ‎{考点:解一元一次不等式组}‎ ‎{题目}20.（2019年天津）（本小题8分）某校为了解初中学生每天在校体育活动的时间（单位：h），随机调查了该校的部分初中学生，根据随机调查结果，绘制出如下的统计图①和图②.请根据相关信息，解答下列问题：‎ ‎ ‎ 图① 图②‎ ‎（I）本次接受调查的初中生人数为 ，图①中m的值为 ；‎ ‎（II）求统计的这组每天在校体育活动时间数据的平均数、众数和中位数；‎ ‎（Ⅲ）根据统计的这组每天在校体育活动时间的样本数据，若该校共有800名初中生，估计该校每天在校体育活动时间大于1h的学生人数.‎ ‎{解析}本题考查了统计图，求平均数、众数、中位数，以及利用样本估计总体.（I）根据公式频率=频数÷样本容量进行计算即可，样本容量=1.2÷20%=40，m%=10÷40=25%，所以m=25，故本小题答案为40、25；（II）根据平均数、众数、中位数的定义计算即可；（Ⅲ）利用样本中体育活动时间大于1h的学生人数的占比对总体作出估计即可.‎ ‎{答案}解： （I）40，25；‎ ‎（II）‎ ‎∵在这组数据中，1.5出现了15次，出现的次数最多，∴这组数据的众数是1.5；‎ ‎∵将这组数据按从小到大的顺序排列，其中处于中间的两个数都是1.5，故这两个数的平均数即这组数据的中位数是1.5.‎ 答：这组数据的平均数、众数、中位数都是1.5h.‎ ‎（III）∵在统计的这组每天在校体育活动时间的样本中，每天在校体育活动时间大于1h的学生人数占的比例为1-10%=90%，∴估计该校800名初中学生中，每天在校体育活动时间大于1h的人数约占90%，‎ 从而可计算得：800×90%=720，‎ 答：该校每天在校体育活动时间大于1h的学生约有720人．‎ ‎{分值}3‎ ‎{章节:[1-10-1]统计调查}‎ ‎{章节:[1-20-1-1]平均数}‎ ‎{章节:[1-20-1-2]中位数和众数}‎ ‎{难度:3-中等难度}‎ ‎{类别:常考题}‎ ‎{考点:用样本估计总体}‎ ‎{考点:扇形统计图}‎ ‎{考点:条形统计图}‎ ‎{考点:加权平均数（频数为权重）}‎ ‎{考点:中位数}‎ ‎{考点:众数}‎ ‎{题目}21.（2019年天津）（本小题10分）已经PA,PB分别与⊙O相切于点A，B，∠APB=80°，C为⊙O上一点.‎ 如图①，求∠ACB的大小；‎ ‎（II）如图②，AE为⊙O的直径，AE与BC相交于点D，若AB=AD，求∠EAC的大小.‎ ‎ 图① 图②‎ ‎{解析}本题考查了切线的性质、切线长定理、圆心角与圆周角的关系等相关知识．（I）连接OA、OB，根据切线的性质结合四边形内角和先求出∠AOB，再利用在同圆或等圆中，一条弧所对的圆周角等于它所对的圆心角的一半即可求出答案；（II）先求出∠PAB=50°，再求出∠BAD=40°，再根据AB=AD求出∠ADB=70°，再根据三角形外角的性质可得∠EAC=∠ADB-∠ACB=20°． ‎ ‎{答案}解：（Ⅰ）连接OA、OB，∵PA，PB是⊙O的切线，∴OA⊥PA，OB⊥PB，∴∠OAP=∠OBP=90°，∵∠APB=80°，∴在四边形OAPB中，∠AOB=360°-∠OAP-∠OBP-∠APB=100°，∴∠ACB=∠AOB=50°；‎ ‎ 图① 图②‎ ‎（II）如图②，∵PA，PB是⊙O的切线，∴PA=PB，∵∠APB=80°，∴∠PAB=∠PBA=50°，由（Ⅰ）知∠PAD=90°，∠ACB=50°，∴∠BAD=∠PAD-∠PAB=40°，∵AB=AD，∴∠ADB=∠B=70°，∵∠ADB=∠EAC+∠ACB，∴∠EAC=∠ADB-∠ACB=20°.‎ ‎{分值}10‎ ‎{章节:[1-24-2-2]直线和圆的位置关系}‎ ‎{难度:3-中等难度} ‎ ‎{类别:常考题}‎ ‎{考点:切线长定理}‎ ‎{题目}22.（2019年天津）（本小题10分）如图，海面上一艘船由西向东航行，在A处测得正东方向上一座灯塔的最高点C的仰角为31°，再向东继续航行30m到达B处，测得该灯塔的最高点C的仰角为45°.根据测得的数据，计算这座灯塔的高度CD(结果取整数).‎ 参考数据： sin31°≈0.52，cos31°≈0.86，tan31°≈0.60 .‎ ‎ ‎ ‎{解析}本题考查了解直角三角形的应用问题（增长率）．设所求灯塔高度为x，利用直角三角形的边角关系表示出AD和BD的长，再列出方程即可求解.‎ ‎{答案}解：设CD=x.在Rt△CAD中，∵tan∠CAD=≈0.60，∴AD=≈.‎ 在Rt△CBD中，∠CBD＝45°，∴BD＝CD=x，∵AD＝AB+BD，∴＝x+30，解得x＝45.‎ 答：这座灯塔的高度CD约为45m．‎ ‎ ‎ ‎{分值}10‎ ‎{章节:[1-28-1-2]解直角三角形}‎ ‎{难度:3-中等难度}‎ ‎{类别:常考题}‎ ‎{章节:[1-28-1-2]解直角三角形}‎ ‎{考点:解直角三角形的应用—测高测距离}‎ ‎{题目}23.（2019年天津）（本小题10分）甲、乙两个批发店销售同一种苹果.在甲批发店，不论一次购买数量是多少，价格均为6元/kg．在乙批发店，一次购买数量不超过50kg时，价格为7元/kg；一次购买数量超过50kg时，其中有50kg的价格仍为7元/kg，超过50kg部分的价格为5元/kg．设小王在同一个批发店一次购买苹果的数量为xkg（x＞0）．‎ ‎（Ⅰ）根据题意填表：‎ 一次购买数量/kg ‎30‎ ‎50‎ ‎150‎ ‎…‎ 甲批发店花费/元 ‎300‎ ‎…‎ 乙批发店花费/元 ‎350‎ ‎…‎ ‎（Ⅱ）设在甲批发店花费y1元，在乙批发店花费y2元，分别求y1，y2关于x的函数解析式；‎ ‎（Ⅲ）根据题意填空：‎ ‎①若小王在甲批发店和在乙批发店一次购买苹果的数量相同，且花费相同，则他在同一个批发店一次购买苹果的数量为　 　kg；‎ ‎②若小王在同一个批发店一次购买苹果的数量为120kg，则他在甲、乙两个批发店中的　 　批发店购买花费少；‎ ‎③若小王在同一个批发店一次购买苹果花费了360元，则他在甲、乙两个批发店中的　 　批发店购买数量多．‎ ‎{解析}本题考查了一次函数的简单应用.（Ⅰ）根据题意计算即可，6×30＝180，6×150＝900，7×30＝210，7×50+5×（150﹣50）＝850，因此本小题答案为：（从左到右，从上往下）依次为180，900，210，850．（Ⅱ）根据题意直接列式即可，甲批发店花费 y1（元）＝6×购买数量x（千克）；而乙批发店花费 y2（元）是购买数量x（千克）的分段函数：花费 y2（元）在一次购买数量不超过50kg时，y2（元）＝7×购买数量x（千克）；一次购买数量超过50kg时，y2（元）＝7‎ ‎×50+5（x﹣50）．（Ⅲ）①根据花费相同，即y1＝y2列方程即可求出相应的x的值；②求出在x＝120时，所对应的y1、y2的值，比较得出结论；‎ ‎③求出当y＝360时，两店所对应的x的值，再通过比较得出结论．‎ ‎{答案}解：（Ⅰ）（从左到右，从上往下）依次为：180，900，210，850；‎ ‎（Ⅱ）y1＝6x （x＞0）；当0＜x≤50时，y2＝7x （0＜x≤50）；当x＞50时，y2＝7×50+5（x﹣50）＝5x+100 （x＞50）.因此y1，y2与x的函数解析式分别为：‎ y1＝6x （x＞0）；.‎ ‎（Ⅲ）①当0＜x≤50时，由题知6x＝7x，解得x＝0，不合题意舍去；当x＞50时，由题知6x＝5x+100，解得x＝100，故他在同一个批发店一次购买苹果的数量为100千克，因此本小题的答案为：100；‎ ‎②当x＝120时，y1＝6×120＝720，y2＝5×120+100＝700，∵720＞700，∴乙批发店花费少．故本小题答案为：乙；‎ ‎③当y1＝6x＝360时，解得x＝60；当y2＝7x =360时，解得x=（大于50，舍去）；当y2＝5x+100＝360时，解得x＝52.∵60＞52，∴甲批发店购买数量多．本小题答案为：甲．‎ ‎{分值}10‎ ‎{章节:[1-19-2-2]一次函数}‎ ‎{{难度:3-中等难度}‎ ‎{类别:常考题}‎ ‎{考点:分段函数的应用}‎ ‎{题目}24.（2019年天津）（本题10分）在平面直角坐标系中，O为原点，点A（6，0），点B在y轴的正半轴上，∠ABO＝30°．矩形CODE的顶点D，E，C分别在OA，AB，OB上，OD＝2．‎ ‎（Ⅰ）如图①，求点E的坐标；‎ ‎（Ⅱ）将矩形CODE沿x轴向右平移，得到矩形C′O′D′E′，点C，O，D，E的对应点分别为C′，O′，D′，E′．设OO′＝t，矩形C′O′D′E′与△ABO重叠部分的面积为S．‎ ‎①如图②，当矩形C′O′D′E′与△ABO重叠部分为五边形时，C′E′，E′D′分别与AB相交于点M，F，试用含有t的式子表示S，并直接写出t的取值范围；‎ ‎②当≤S≤5时，求t的取值范围（直接写出结果即可）．‎ ‎ ‎ ‎ 图① 图②‎ ‎{解析}一次函数图像与几何图形的综合问题．（Ⅰ）先求出AD的长，再解直角三角形ADE求出ED，即可得答案；‎ ‎（Ⅱ）①将阴影部分的面积化为矩形C′O′D′E′与ME′F的面积的差来求即可得S；利用点C′、E′在直线AB上这两种极端情况，可求得t的取值范围.由（I）知当点E′落在AB上时，t=0；当点C′落在AB上时，C′O′=4，可求出A′O′=4，从而得到C′O′=2，故t的取值范围是0＜t＜2.‎ ‎②先通过计算①中函数的值的范围确定当≤S≤5时，t超过2.‎ 再分重叠部分为直角梯形、直角三角形两种情况进行探究，先分别确定重叠部分形状，再求出S与t的函数关系式.然后计算当S为5、时的t的值，就能得到t的取值范围．‎ ‎{答案}解： （I）由A（6，0），得OA=6，又OD=2，∴AD=OA-OD=4.在矩形CODE中，由DE∥CO，得∠AED=∠ABO=30°，∴在Rt△AED中，AE=2AD=8.∴由勾股定理得：ED=AE-AD=4，有CO=4‎ ‎∴E（2，4）；‎ ‎（II）①由平移可知，，=4，，由∥BO，得∠=∠ABO=30°，在Rt△MF中，MF=2，∴由勾股定理得.‎ ‎∴，而，‎ ‎∴（0＜t＜2）.‎ ‎②由①知当时，，且S随着t的增大而减小.当t=0时，S最大；当t=2时，S最小.∴当≤S≤5时，t＞2.当2＜t＜4时，矩形C′O′D′E′与△ABO重叠部分为直角梯形，如图③，设O′C′交AB于N，D′E′仍交AB于F.‎ ‎∵AD′=4-t，AO′=6-t，∴D′F=（4-t），O′N=（6-t），O′D′=2，‎ ‎∴S=[（4-t）+（6-t）]×2=，显然S随着t的增大而减小.‎ 当S==5时，t=2.5；当t=4时，s=2,∴当2＜t＜4时，S＞2．‎ ‎∴当2＜t＜4时，符合≤S≤5的t的取值范围是2.5≤t＜4；‎ ‎（图③） （图④）‎ 当4≤t＜6时，矩形C′O′D′E′与△ABO重叠部分为直角三角形，如图④，设O′C′仍交AB于N，则AO′=6-t，O′N=（6-t），‎ ‎∴S=（6-t）·（6-t）=（6-t）2，显然S随着t的增大而减小.‎ 当S=（6-t）2=时，解得（舍去），.∴.‎ ‎∴当4≤t＜6时，符合≤S≤5的t的取值范围是4≤t≤.‎ 综上，本小题答案为：.‎ ‎{分值}10‎ ‎{章节:[1-19-4]课题学习 选择方案}‎ ‎{难度:4-较高难度}‎ ‎{类别:常考题}‎ ‎{考点:一次函数与几何图形综合}‎ ‎{题目}25.（本小题10分）已知抛物线y＝x2﹣bx+c（b，c为常数，b＞0）经过点A（﹣1，0），点M（m，0）是x轴正半轴上的动点．‎ ‎（Ⅰ）当b＝2时，求抛物线的顶点坐标；‎ ‎（Ⅱ）点D（b，yD）在抛物线上，当AM＝AD，m＝5时，求b的值；‎ ‎（Ⅲ）点Q（，yQ）在抛物线上，当AM+2QM的最小值为时，求b的值．‎ ‎{解析}本题考查了二次函数的图像与性质，综合性较强．（Ⅰ）将点A（﹣1，0）代入y＝x2﹣2x+c，求出c的值，进一步便可根据抛物线的解析式及求出其顶点坐标；‎ ‎（Ⅱ）将点D（b，yD）代入抛物线y＝x2﹣bx﹣b﹣1，求出点D，利用条件AM＝AD构造方程即可求出b的值；‎ ‎（Ⅲ）先变形得AM+2QM=2（AM+QM），再通过构造以AM为斜边的等腰直角三角形，将AM+QM及其最小值通过图形表示出来，“以形显数”，再利用等腰直角三角形的性质及点Q的坐标列方程组求出m和b，就能解决问题.‎ ‎{答案}解： （I）当b=2时，抛物线为y＝x2﹣2x+c，将A（-1，0）代入，得1-2+c=0,∴c= - 3 ,∴抛物线解析式为，∴其顶点坐标为（1，- 4）；‎ ‎（II）A（-1，0）代入抛物线解析式得，1+b+c＝0，∴c＝﹣b﹣1，∴抛物线为y＝x2﹣bx﹣b﹣1.‎ 设抛物线与y轴交于点C，则C（0,﹣b﹣1）.当x=b时，yD＝b2﹣b•b﹣b﹣1＝﹣b﹣1，∴D（b，﹣b﹣1）.∵b＞0，∴D与C不重合，点D在第四象限.如图①，过点D作DE⊥x轴，垂足为E，则点E（b，0），∴AE＝DE＝b+1，∴AD=AE=（b+1）.∵m＝5，∴M（m，0），∴AM=6.由已知AM＝AD，∴（b+1）=6，∴b＝3‎2‎‎-‎1；‎ 图① 图②‎ ‎（Ⅲ）把Q（，）代入，得，∵b＞0，抛物线对称轴为直线x=，∴点Q（，）在第四象限、对称轴右侧.‎ 令AM+2QM=w，则w=AM+2QM=2（AM+QM）.‎ 如图，在x轴上方取一点N，使得△AMN是以AM为斜边的等腰直角三角形，则MN=AM，此时AM+QM=MN+QM≥NQ,∴w最小=2NQ=,∴NQ=.∵∠MNH=45°，∴△NQH为等腰直角三角形，∴NH=QH=,∵AF=NF=AM=(m+1).‎ ‎∴,解得.‎ 综上，b=4.‎ ‎{分值}10‎ ‎{章节:[1-22-2]二次函数与一元二次方程}‎ ‎{难度:5-高难度}‎ ‎{类别:高度原创}‎ ‎{类别:发现探究}‎ ‎{考点:其他二次函数综合题}‎