2020年苏教版中考数学第一次模拟考试及答案 15页

苏教版2020年中考数学第一次模拟考试 数 学 ‎（考试时间：120分钟 试卷满分：120分）‎ 注意事项：‎ ‎1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。‎ ‎2．回答第Ⅰ卷时，选出每小题答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。写在本试卷上无效。‎ ‎3．回答第Ⅱ卷时，将答案写在答题卡上。写在本试卷上无效。‎ ‎4．考试结束后，将本试卷和答题卡一并交回。‎ ‎5．考试范围：中考全部内容。‎ 第Ⅰ卷 一、选择题（本大题共6小题，每小题2分，共12分．在每小题给出的四个选项中，只有一个选项是符合题目要求的）‎ ‎1．据报道，人类首张黑洞照片于北京时间2019年4月10日在全球六地同步发布，该黑洞位于室女座一个巨椭圆星系M87的中心，距离地球5500万光年．其中5500万用科学记数法表示为 A．55×106 B．5.5×106 C．5.5×107 D．5.5×108‎ ‎2．实数，，在数轴上的对应点的位置如图所示，则正确的结论是 A． B． C． D．‎ ‎3．某小组7名同学在一周内参加家务劳动的时间如下表所示，关于“劳动时间”的这组数据，以下说法正确的是 劳动时间（小时）‎ ‎3‎ ‎3．5‎ ‎4‎ ‎4．5‎ 人数 ‎1‎ ‎1‎ ‎3‎ ‎2‎ A．中位数是4，众数是4 B．中位数是3.5，众数是4‎ C．平均数是3.5，众数是4 D．平均数是4，众数是3.5‎ ‎4．如图，中，，，，点在上，延长至点，使，是的中点，连接，则的长是 A． B． C． D．‎ ‎5．如图，点D在半圆O上，半径OB=2，AD=10，点C在弧BD上移动，连接AC，H是AC上一点，∠DHC=90°，连接BH，点C在移动的过程中，BH的最小值是 A．5 B．6 C．7 D．8‎ ‎6．如图，甲、丙两地相距500km，一列快车从甲地驶往丙地，途中经过乙地；一列慢车从乙地驶往丙地，两车同时出发，同向而行，折线ABCD表示两车之间的距离y（km）与慢车行驶的时间为x（h）之间的函数关系．根据图中提供的信息，下列说法不正确的是 A．甲、乙两地之间的距离为200km ‎ B．快车从甲地驶到丙地共用了2.5h C．快车速度是慢车速度的1.5倍 ‎ D．快车到达丙地时，慢车距丙地还有50km 第Ⅱ卷 二、填空题（本大题共10小题，每小题2分，共20分）‎ ‎7．的平方根是____．‎ ‎8．如果分式有意义，那么x的取值范围是_____．‎ ‎9．因式分解：________．‎ ‎10．计算的结果是_____．‎ ‎11．已知x1，x2是关于x的一元二次方程x2+2x+k﹣1=0的两个实数根，且x12+x22﹣x1x2=13，则k的值为___．‎ ‎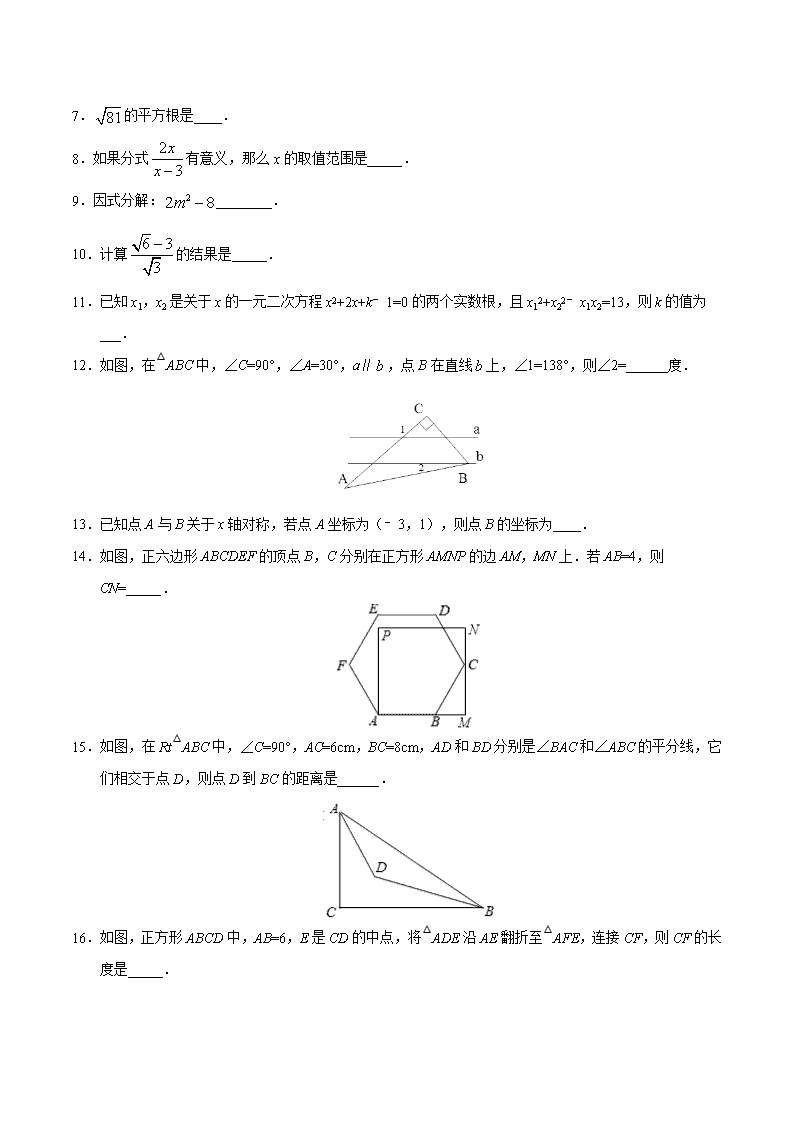12．如图，在△ABC中，∠C=90°，∠A=30°，a∥，点B在直线上，∠1=138°，则∠2=______度．‎ ‎13．已知点A与B关于x轴对称，若点A坐标为（﹣3，1），则点B的坐标为____．‎ ‎14．如图，正六边形ABCDEF的顶点B，C分别在正方形AMNP的边AM，MN上．若AB=4，则CN=_____．‎ ‎15．如图，在Rt△ABC中，∠C=90°，AC=6cm，BC=8cm，AD和BD分别是∠BAC和∠ABC的平分线，它们相交于点D，则点D到BC的距离是______．‎ ‎16．如图，正方形ABCD中，AB=6，E是CD的中点，将△ADE沿AE翻折至△AFE，连接CF，则CF的长度是_____．‎ 三、解答题（本大题共11小题，共88分．解答应写出文字说明、证明过程或演算步骤）‎ ‎17．（7分）化简：‎ ‎18．（7分）化简：‎ ‎19．（8分）为加快城市群的建设与发展，在A、B两城市间新建一条城际铁路，建成后，铁路运行里程由现在的210km缩短至180km，平均时速要比现行的平均时速快200km，运行时间仅是现行时间的，求建成后的城际铁路在A、B两地的运行时间？‎ ‎20．（8分）射击爱好者甲、乙的近8次比赛成绩的分析如下表（成绩单位：环）：‎ 次序 一 二 三 四 五 六 七 八 平均数 方差 甲 ‎9‎ ‎6‎ ‎6‎ ‎8‎ ‎7‎ ‎6‎ ‎6‎ ‎8‎ a ‎1.25‎ 乙 ‎7‎ ‎7‎ ‎4‎ ‎5‎ ‎8‎ ‎7‎ ‎10‎ ‎8‎ ‎7‎ b ‎（1）求a、b的值；‎ ‎（2）从两个不同角度评价两人的射击水平．‎ ‎21．（8分）在一个不透明的布袋中，有个红球，个白球，这些球除颜色外都相同．‎ ‎（1）搅匀后从中任意摸出个球，摸到红球的概率是________；‎ ‎（2）搅匀后先从中任意摸出个球（不放回），再从余下的球中任意摸出个球．求两次都摸到红球的概率．（用树状图或表格列出所有等可能出现的结果）‎ ‎22．（8分）如图，AC为矩形ABCD的对角线，将边AB沿AE折叠，使点B落在AC上的点M处，将边CD沿CF折叠，使点D落在AC上的点N处．‎ ‎（1）求证：四边形AECF是平行四边形；‎ ‎（2）当∠BAE为多少度时，四边形AECF是菱形？请说明理由．‎ ‎23．（8分）如图，某大楼的顶部竖有一块宣传牌CD．小明在山坡的坡脚A处测得宣传牌底部D的仰角为63°，沿山坡向上走到B处测得宣传牌顶部C的仰角为45°．已知山坡AB的坡度i=1：，AB=10米，CD=2米．‎ ‎（1）求点B距地面的高度；‎ ‎（2）求大楼DE的高度．（测角器的高度忽略不计，结果精确到0．1米，参考数据tan63°≈2，≈1．732）‎ ‎24．（8分）如图，△ABC中，AB=AC，以AB为直径的⊙O与BC相交于点D，与CA的延长线相交于点E，过点D作DF⊥AC于点F．‎ ‎（1）证明：DF是⊙O的切线；‎ ‎（2）若AC=3AE，FC=6，求AF的长．‎ ‎25．（8分）甲、乙两人在笔直的道路AB上相向而行，甲骑自行车从A地到B地，乙驾车从B地到A地，假设他们分别以不同的速度匀速行驶，甲先出发6分钟后，乙才出发，乙的速度为千米/分，在整个过程中，甲、乙两人之间的距离y（千米）与甲出发的时间x（分）之间的部分函数图象如图．‎ ‎（1）A、B两地相距____千米，甲的速度为____千米/分；‎ ‎（2）求线段EF所表示的y与x之间的函数表达式；‎ ‎（3）当乙到达终点A时，甲还需多少分钟到达终点B？‎ ‎26．（10分）定义：到三角形的两边距离相等的点，叫做此三角形的准内心，例如：如图1，PD⊥AC，PE⊥AB，垂足分别为点D、E，若PD=PE，则点P为△ABC的准内心．‎ ‎（1）应用：如图2，CD为等边三角形ABC的高，准内心P在高CD上，且PD=AB，求∠APB的度数．‎ ‎（2）探究：如图3，已知△ABC为直角三角形，斜边BC=5，AB=3，准内心P在AC边上（不与点A、C重合），求PA的长．‎ ‎27．（10分）如图，抛物线y=ax2+bx+3的图象经过点A（1，0），B（3，0），交y轴于点C，顶点是D．‎ ‎（1）求抛物线的表达式和顶点D的坐标；‎ ‎（2）在x轴上取点F，在抛物线上取点E，使以点C、D、E、F为顶点的四边形是平行四边形，求点E的坐标；‎ ‎（3）将此抛物线沿着过点（0，2）且垂直于y轴的直线翻折，E为所得新抛物线x轴上方一动点，过E作x轴的垂线，交x轴于G，交直线l：y=-x-1于点F，以EF为直径作圆在直线l上截得弦MN，求弦MN长度的最大值．‎ 学科网2020年中考数学第一次模拟考试【江苏卷】‎ 数学·参考答案 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ C B A A D C ‎7．±3 8．x≠3 9． 10． 11．﹣2‎ ‎12．12 13．（﹣3，﹣1） 14． 15．2cm 16．‎ ‎17．【解析】原式．‎ ‎18．【解析】‎ ‎=‎ ‎=a．‎ ‎19．【解析】设城际铁路现行速度是xkm/h，则建成后时速是（x+200）xkm/h；‎ 根据题意得：×=，‎ 解得：x=70，‎ 经检验：x=70是原方程的解，且符合题意，‎ ‎∴==（h）‎ 答：建成后的城际铁路在A、B两地的运行时间为h．‎ ‎20．【解析】（1），‎ ‎．‎ ‎（2）评价角度不唯一，以下答案供参考：‎ 两人平均数都是7环，说明两人平均水平相当；‎ 甲的方差小于乙的方差，说明乙的成绩不如甲稳定．‎ ‎21．【解析】（1）一般地，如果在一次试验中，有种可能的结果，并且它们发生的可能性都相等，事件包含其中的种结果，那么事件发生的概率为，则摸到红球的概率为．‎ ‎（2）两次摸球的所有可能的结果如下：‎ 有树状图可知，共有种等可能的结果，两次都摸出红球有种情况，‎ 故（两次都摸处红球）．‎ ‎22．【解析】（1）∵四边形ABCD为矩形，‎ ‎∴AB=CD，AD∥BC，∠B=∠D=90°，∠BAC=∠DCA．‎ 由翻折的性质可知：∠EAB=∠BAC，∠DCF=∠DCA．‎ ‎∴∠EAB=∠DCF．‎ 在△ABE和△CDF中，‎ ‎∴△ABE≌△CDF（ASA），‎ ‎∴DF=BE．‎ ‎∴AF=EC．‎ 又∵AF∥EC，‎ ‎∴四边形AECF是平行四边形；‎ ‎（2）当∠BAE=30°时，四边形AECF是菱形，‎ 理由：由折叠可知，∠BAE=∠CAE=30°，‎ ‎∵∠B=90°，‎ ‎∴∠ACE=90°-30°=60°，‎ 即∠CAE=∠ACE，‎ ‎∴EA=EC，‎ ‎∵四边形AECF是平行四边形，‎ ‎∴四边形AECF是菱形．‎ ‎23．【解析】（1）作BG⊥AE于点G，由山坡AB的坡度i=1：，‎ 设BG=x，则AG=x，‎ ‎∵AB=10，‎ ‎∴x2+（x）2=102，‎ 解得x=5，即BG=5，‎ ‎∴点B距地面的高度为：5米；‎ ‎（2）由（1）可得AG=BG=，作BF⊥DE交DE于点F，‎ 设DE=x米，在Rt△ADE中，‎ ‎∵tan∠DAE=，‎ ‎∴AE=≈，‎ ‎∴EF=BG=5，BF=AG+AE=，‎ ‎∵∠CBF=45°，‎ ‎∴CF=BF，‎ ‎∴CD+DE﹣EF=BF，‎ ‎∴2+x﹣5=，‎ 解得：x=≈23．3（米）‎ 答：大楼DE的高度约为23．3米．‎ ‎24．【解析】（1）如图1，连接OD，‎ ‎∵OB=OD，‎ ‎∴∠B=∠ODB，‎ ‎∵AB=AC，‎ ‎∴∠B=∠C，‎ ‎∴∠ODB=∠C，‎ ‎∴OD∥AC，‎ ‎∵DF⊥AC，‎ ‎∴OD⊥DF，‎ ‎∴DF是⊙O的切线；‎ ‎（2）解：如图2，连接BE，AD，‎ ‎∵AB是直径，‎ ‎∴∠AEB=90°，‎ ‎∵AB=AC，AC=3AE，‎ ‎∴AB=3AE，CE=4AE，‎ ‎∴，‎ ‎∴，‎ ‎∵∠DFC=∠AEB=90°，‎ ‎∴DF∥BE，‎ ‎∴△DFC∽△BEC，‎ ‎∴，‎ ‎∵CF=6，‎ ‎∴DF=3，‎ ‎∵AB是直径，‎ ‎∴AD⊥BC，‎ ‎∵DF⊥AC，‎ ‎∴∠DFC=∠ADC=90°，∠DAF=∠FDC，‎ ‎∴△ADF∽△DCF，‎ ‎∴，‎ ‎∴DF2=AF•FC，‎ ‎∴，‎ ‎∴AF=3．‎ ‎25．【解析】（1）观察图象知A、B两地相距为24km，‎ ‎∵甲先行驶了2千米，由横坐标看出甲行驶2千米用了6分钟，‎ ‎∴甲的速度是千米/分钟；‎ 故答案为24，；‎ ‎（2）设甲乙经过a分钟相遇，根据题意得，‎ ‎，解答a=18，‎ ‎∴F（18，0），‎ 设线段EF表示的y与x之间的函数表达式为y=kx+b，根据题意得，‎ ‎，解得，‎ ‎∴线段EF表示的y与x之间的函数表达式为y=﹣x+33；‎ ‎（3）相遇后乙到达A地还需：（18×）÷=4（分钟），‎ 相遇后甲到达B站还需：（12×）÷=54（分钟）‎ 当乙到达终点A时，甲还需54﹣4=50分钟到达终点B．‎ ‎26．【解析】（1）∵准内心P在高CD上，‎ ‎∴①点P为∠CAD的角平分线与CD的交点，‎ ‎∵△ABC是等边三角形，‎ ‎∴∠PAD=∠PAC=30°，‎ ‎∵CD为等边三角形ABC的高，‎ ‎∴AD=DP，AD=BD，‎ 与已知PD=AB矛盾，‎ ‎∴点P不可能为∠CAD的角平分线与CD的交点，‎ 同理可知②点P不可能为∠CBD的角平分线与CD的交点，‎ ‎③∵CD⊥AB，‎ ‎∴点P为∠BCA的平分线，‎ 此时，点P到AC和BC的距离相等，‎ ‎∵PD=AB，‎ ‎∴PD=AD=BD，‎ ‎∴∠APD=∠BPD=45°，‎ ‎∴∠APB=90°；‎ ‎（2）∵BC=5，AB=3，‎ ‎∴AC==4，‎ ‎∵准内心在AC边上，（不与点A，B重合），‎ ‎∴点P为∠CBA的平分线与AC的交点，‎ 作PD⊥BC与点D，‎ ‎∴PA=PD，BD=BA=3，‎ 设PA=x，则x2+22=（4﹣x）2，‎ ‎∴x=，即PA=．‎ ‎27．【解析】（1）∵抛物线y=ax2+bx+3的图象经过点A（1，0），B（3，0），‎ ‎∴．‎ 解得．‎ 抛物线的表达式为：y=x2-4x+3；‎ ‎（2）如图1，当CD为平行四边形的对角线时，‎ 设点E的坐标为（x，x2-4x+3），‎ 则CD中点的坐标为（1，1），该点也为EF的中点．‎ 即：x2-4x+3=2×1，解得：x=2±，‎ E的坐标为（2+，2）或（2-，2）；‎ 如图2，当CD为平行四边形的一条边时，‎ 设点F坐标为（m，0），‎ 点D向左平移2个单位、向上平移4个单位，得到点C，‎ 同样点F向左平移2个单位、向上平移4个单位，得到点E（m-2，4），‎ 将点E坐标代入二次函数表达式并解得：m=4±，‎ 则点E（2+，4）或（2-，4）；‎ 故点E的坐标为（2+，2）或（2-，2）或（2+，4）或（2-，4）；‎ ‎（3）抛物线沿着过点（0，2）且垂直与y轴的直线翻折后，顶点坐标为（2，5），‎ 则新抛物线的表达式为：y=-（x-2）2+5=-x2+4x+1．‎ 设点E的坐标为（x，-x2+4x+1），则点F（x，-x-1），‎ EF=-x2+4x+1-（-x-1）=-x2+x+2．‎ 设直线y=-x-1与x轴交于点Q．‎ MN=EF•cos∠QFG=（-x2+x+2）=-（x-）2+．‎ 由二次函数性质可知，MN的最大值为．‎