2020年山东省临沂市中考数学试卷【含答案；word版本试题；可编辑】 9页

‎2020年山东省临沂市中考数学试卷 一、选择题（本大题共14小题，每小题3分，共42分）在每小题所给出的四个选项中，只有一项是符合题目要求的．‎ ‎1. 下列温度比‎-2‎​‎‎∘‎C低的是（ ）‎ A.‎-3‎​‎‎∘‎C B.‎-1‎​‎‎∘‎C C.‎1‎​‎‎∘‎C D.‎‎3‎​‎‎∘‎C ‎2. 下列交通标志中，是中心对称图形的是（ ）‎ A. B. C. D.‎ ‎3. 如图，数轴上点A对应的数是‎3‎‎2‎，将点A沿数轴向左移动‎2‎个单位至点B，则点B对应的数是（ ）‎ A.‎-‎‎1‎‎2‎ B.‎-2‎ C.‎7‎‎2‎ D.‎‎1‎‎2‎ ‎4. 根据图中三视图可知该几何体是（ ）‎ A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱 ‎5. 如图，在‎△ABC中，AB＝AC，‎∠A＝‎40‎‎∘‎，CD // AB，则‎∠BCD＝（ ）‎ A.‎40‎‎∘‎ B.‎50‎‎∘‎ C.‎60‎‎∘‎ D.‎‎70‎‎∘‎ ‎6. 计算‎(-2a‎3‎‎)‎‎2‎÷‎a‎2‎的结果是（ ）‎ A.‎-2‎a‎3‎ B.‎-2‎a‎4‎ C.‎4‎a‎3‎ D.‎‎4‎a‎4‎ ‎7. 设a=‎7‎+2‎．则（ ）‎ A.‎2‎S‎2‎ B.‎S‎1‎‎+S‎2‎<‎S‎2‎ C.S‎1‎‎+S‎2‎=‎S‎2‎ D.S‎1‎‎+‎S‎2‎的大小与P点位置有关 ‎13. 计算xx-1‎‎-‎yy-1‎的结果为（ ）‎ A.‎-x+y‎(x-1)(y-1)‎ B.‎x-y‎(x-1)(y-1)‎ C.‎-x-y‎(x-1)(y-1)‎ D.‎x+y‎(x-1)(y-1)‎ ‎14. 如图，在‎⊙O中，AB为直径，‎∠AOC＝‎80‎‎∘‎．点D为弦AC的中点，点E为BC上任意一点．则‎∠CED的大小可能是（ ）‎ A.‎10‎‎∘‎ B.‎20‎‎∘‎ C.‎30‎‎∘‎ D.‎‎40‎‎∘‎ 二、填空题（本大题共5小题，每小题3分，共15分）‎ ‎15. 不等式‎2x+1<0‎的解集是________‎<-‎‎1‎‎2‎ ．‎ ‎16. 若a+b＝‎1‎，则a‎2‎‎-b‎2‎+2b-2‎＝________．‎ ‎17. 点‎(-‎1‎‎2‎, m)‎和点‎(2, n)‎在直线y＝‎2x+b上，则m与n的大小关系是________．‎ ‎18. 如图，在‎△ABC中，D、E为边AB的三等分点，EF // DG // AC，H为AF与DG的交点．若AC＝‎6‎，则DH＝________．‎ ‎19. 我们知道，两点之间线段最短，因此，连接两点间线段的长度叫做两点间的距离；同理，连接直线外一点与直线上各点的所有线段中，垂线段最短，因此，直线外一点到这条直线的垂线段的长度，叫做点到直线的距离．类似地，连接曲线外一点与曲线上各点的所有线段中，最短线段的长度，叫做点到曲线的距离．依此定义，如图，在平面直角坐标系中，点A(2, 1)‎到以原点为圆心，以‎1‎为半径的圆的距离为________．‎ ‎ 9 / 9‎ 三、解答题（本大题共7小题，共63分）‎ ‎20. 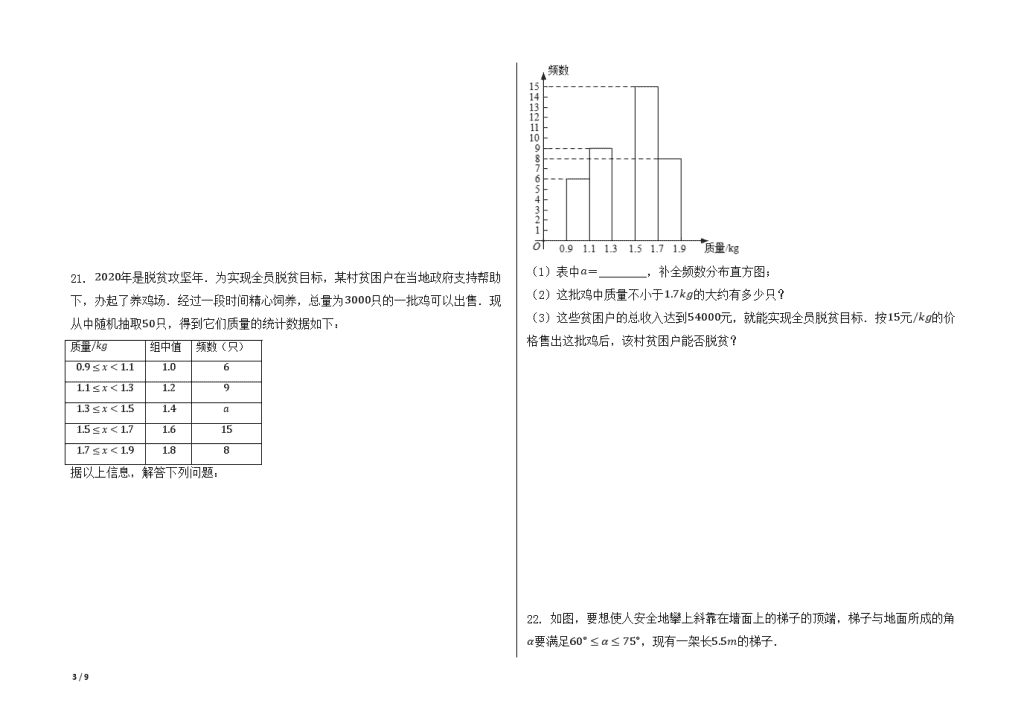计算：‎(‎1‎‎3‎-‎‎1‎‎2‎‎)‎‎2‎‎+‎2‎‎2‎×‎1‎‎6‎-sin‎60‎‎∘‎．‎ ‎21. ‎2020‎年是脱贫攻坚年．为实现全员脱贫目标，某村贫困户在当地政府支持帮助下，办起了养鸡场．经过一段时间精心饲养，总量为‎3000‎只的一批鸡可以出售．现从中随机抽取‎50‎只，得到它们质量的统计数据如下：‎ 质量‎/kg 组中值 频数（只）‎ ‎0.9≤x<1.1‎ ‎1.0‎ ‎6‎ ‎1.1≤x<1.3‎ ‎1.2‎ ‎9‎ ‎1.3≤x<1.5‎ ‎1.4‎ a ‎1.5≤x<1.7‎ ‎1.6‎ ‎15‎ ‎1.7≤x<1.9‎ ‎1.8‎ ‎8‎ 据以上信息，解答下列问题：‎ ‎（1）表中a＝________，补全频数分布直方图；‎ ‎（2）这批鸡中质量不小于‎1.7kg的大约有多少只？‎ ‎（3）这些贫困户的总收入达到‎54000‎元，就能实现全员脱贫目标．按‎15‎元‎/kg的价格售出这批鸡后，该村贫困户能否脱贫？‎ ‎ 9 / 9‎ ‎22. 如图，要想使人安全地攀上斜靠在墙面上的梯子的顶端，梯子与地面所成的角α要满足‎60‎‎∘‎‎≤α≤‎‎75‎‎∘‎，现有一架长‎5.5m的梯子．‎ ‎（1）使用这架梯子最高可以安全攀上多高的墙（结果保留小数点后一位）？‎ ‎（2）当梯子底端距离墙面‎2.2m时，α等于多少度（结果保留小数点后一位）？此时人是否能够安全使用这架梯子？‎ ‎（参考数据：sin‎75‎‎∘‎≈0.97‎，cos‎75‎‎∘‎≈0.26‎，tan‎75‎‎∘‎≈3.73‎，sin‎23.6‎‎∘‎≈0.40‎，cos‎66.4‎‎∘‎≈0.40‎，tan‎21.8‎‎∘‎≈0.40‎．）‎ ‎23. 已知蓄电池的电压为定值，使用蓄电池时，电流I（单位：A）与电阻R（单位：Ω）是反比例函数关系．当R＝‎4Ω时，I＝‎9A．‎ ‎（1）写出I关于R的函数解析式；‎ ‎（2）完成下表，并在给定的平面直角坐标系中画出这个函数的图象；‎ R/Ω ‎…‎ ‎________‎ ‎________‎ ‎________‎ ‎________‎ ‎________‎ ‎________‎ ‎________‎ ‎________‎ ‎…‎ I/A ‎…‎ ‎________‎ ‎________‎ ‎________‎ ‎________‎ ‎________‎ ‎________‎ ‎________‎ ‎________‎ ‎…‎ ‎（3）如果以此蓄电池为电源的用电器的限制电流不能超过‎10A，那么用电器可变电阻应控制在什么范围内？‎ ‎ 9 / 9‎ ‎24. 已知‎⊙‎O‎1‎的半径为r‎1‎，‎⊙‎O‎2‎的半径为r‎2‎．以O‎1‎为圆心，以r‎1‎‎+‎r‎2‎的长为半径画弧，再以线段O‎1‎O‎2‎的中点P为圆心，以‎1‎‎2‎O‎1‎O‎2‎的长为半径画弧，两弧交于点A，连接O‎1‎A，O‎2‎A，O‎1‎A交‎⊙‎O‎1‎于点B，过点B作O‎2‎A的平行线BC交O‎1‎O‎2‎于点C．‎ ‎（1）求证：BC是‎⊙‎O‎2‎的切线；‎ ‎（2）若r‎1‎＝‎2‎，r‎2‎＝‎1‎，O‎1‎O‎2‎＝‎6‎，求阴影部分的面积．‎ ‎25. 已知抛物线y＝ax‎2‎-2ax-3+2a‎2‎(a≠0)‎．‎ ‎（1）求这条抛物线的对称轴；‎ ‎（2）若该抛物线的顶点在x轴上，求其解析式；‎ ‎（3）设点P(m, y‎1‎)‎，Q(3, y‎2‎)‎在抛物线上，若y‎1‎‎<‎y‎2‎，求m的取值范围．‎ ‎ 9 / 9‎ ‎26. 如图，菱形ABCD的边长为‎1‎，‎∠ABC＝‎60‎‎∘‎，点E是边AB上任意一点（端点除外），线段CE的垂直平分线交BD，CE分别于点F，G，AE，EF的中点分别为M，N．‎ ‎（1）求证：AF＝EF；‎ ‎（2）求MN+NG的最小值；‎ ‎（3）当点E在AB上运动时，‎∠CEF的大小是否变化？为什么？‎ ‎ 9 / 9‎ 参考答案与试题解析 ‎2020年山东省临沂市中考数学试卷 一、选择题（本大题共14小题，每小题3分，共42分）在每小题所给出的四个选项中，只有一项是符合题目要求的．‎ ‎1.A ‎2.B ‎3.A ‎4.B ‎5.D ‎6.D ‎7.C ‎8.B ‎9.C ‎10.B ‎11.D ‎12.C ‎13.A ‎14.C 二、填空题（本大题共5小题，每小题3分，共15分）‎ ‎15.‎x ‎16.‎‎-1‎ ‎17.‎m0)‎；‎ ‎3‎‎,‎4‎,‎5‎,‎6‎,‎8‎,‎9‎,‎10‎,‎12‎,‎12‎,‎9‎,‎7.2‎,‎6‎,‎4.5‎,‎4‎,‎3.6‎,‎‎3‎ ‎∵ I≤10‎，I=‎‎36‎R，‎ ‎∴ ‎36‎R‎≤10‎，‎ ‎∴ R≥3.6‎，‎ 即用电器可变电阻应控制在不低于‎3.6‎欧的范围内．‎ ‎24.证明：连接AP，‎ ‎∵ 以线段O‎1‎O‎2‎的中点P为圆心，以‎1‎‎2‎O‎1‎O‎2‎的长为半径画弧，‎ ‎∴ O‎1‎P＝AP＝O‎2‎P=‎‎1‎‎2‎O‎1‎O‎2‎，‎ ‎∴ ‎∠O‎1‎AO‎2‎＝‎90‎‎∘‎，‎ ‎∵ BC // O‎2‎A，‎ ‎∴ ‎∠O‎1‎BC＝‎∠O‎1‎AO‎2‎＝‎90‎‎∘‎，‎ 过点O‎2‎作O‎2‎D⊥BC交BC的延长线于点D，‎ ‎∴ 四边形ABDO‎2‎是矩形，‎ ‎∴ AB＝O‎2‎D，‎ ‎∵ O‎1‎A＝r‎1‎‎+‎r‎2‎，‎ ‎∴ O‎2‎D＝r‎2‎，‎ ‎∴ BC是‎⊙‎O‎2‎的切线；‎ ‎∵ r‎1‎＝‎2‎，r‎2‎＝‎1‎，O‎1‎O‎2‎＝‎6‎，‎ ‎∴ O‎1‎A=‎‎1‎‎2‎O‎1‎O‎2‎，‎ ‎∴ ‎∠AO‎2‎C＝‎30‎‎∘‎，‎ ‎∵ BC // O‎2‎A，‎ ‎∴ ‎∠BCE＝AO‎2‎C＝‎30‎‎∘‎，‎ ‎∴ O‎1‎C＝‎2O‎1‎B＝‎4‎，‎ ‎∴ BC=O‎1‎C‎2‎‎-‎O‎1‎B‎2‎=‎4‎‎2‎‎-‎‎2‎‎2‎=2‎‎3‎，‎ ‎∴ S阴影‎=S‎△O‎1‎BC-SBO‎1‎E=‎1‎‎2‎O‎1‎B⋅BC-‎60π×‎r‎1‎‎2‎‎360‎=‎1‎‎2‎×2×2‎3‎-‎60×π×‎‎2‎‎2‎‎360‎=2‎3‎-‎2‎‎3‎π．‎ ‎25.∵ 抛物线y＝ax‎2‎-2ax-3+2‎a‎2‎＝a(x-1‎)‎‎2‎+2a‎2‎-a-3‎．‎ ‎∴ 抛物线的对称轴为直线x＝‎1‎；‎ ‎∵ 抛物线的顶点在x轴上，‎ ‎∴ ‎2a‎2‎-a-3‎＝‎0‎，‎ 解得a=‎‎3‎‎2‎或a＝‎-1‎，‎ ‎∴ 抛物线为y=‎3‎‎2‎x‎2‎-3x+‎‎3‎‎2‎或y＝‎-x‎2‎+2x-1‎；‎ ‎∵ 抛物线的对称轴为x＝‎1‎，‎ 则Q(3, y‎2‎)‎关于x＝‎1‎对称点的坐标为‎(-1, y‎2‎)‎，‎ ‎∴ 当a>0‎，‎-13‎时，y‎1‎‎<‎y‎2‎．‎ ‎26.连接CF，‎ ‎∵ FG垂直平分CE，‎ ‎∴ CF＝EF，‎ ‎ 9 / 9‎ ‎∵ 四边形ABCD为菱形，‎ ‎∴ A和C关于对角线BD对称，‎ ‎∴ CF＝AF，‎ ‎∴ AF＝EF；‎ 连接AC，交BD于点O，‎ ‎∵ M和N分别是AE和EF的中点，点G为CE中点，‎ ‎∴ MN=‎1‎‎2‎AF，NG=‎1‎‎2‎CF，即MN+NG=‎1‎‎2‎(AF+CF)‎，‎ 当点F与菱形ABCD对角线交点O重合时，‎ AF+CF最小，即此时MN+NG最小，‎ ‎∵ 菱形ABCD边长为‎1‎，‎∠ABC＝‎60‎‎∘‎，‎ ‎∴ ‎△ABC为等边三角形，AC＝AB＝‎1‎，‎ 即MN+NG的最小值为‎1‎‎2‎；‎ 不变，理由是：‎ 延长EF，交DC于H，‎ ‎∵ ‎∠CFH＝‎∠FCE+∠FEC，‎∠AFH＝‎∠FAE+∠FEA，‎ ‎∴ ‎∠AFC＝‎∠FCE+∠FEC+∠FAE+∠FEA，‎ ‎∵ 点F在菱形ABCD对角线BD上，根据菱形的对称性可得：‎ ‎∠AFD‎＝‎∠CFD=‎1‎‎2‎∠AFC，‎ ‎∵ AF＝CF＝EF，‎ ‎∴ ‎∠AEF＝‎∠EAF，‎∠FEC＝‎∠FCE，‎ ‎∴ ‎∠AFD＝‎∠FAE+∠ABF＝‎∠FEA+∠CEF，‎ ‎∴ ‎∠ABF＝‎∠CEF，‎ ‎∵ ‎∠ABC＝‎60‎‎∘‎，‎ ‎∴ ‎∠ABF＝‎∠CEF＝‎30‎‎∘‎，为定值．‎ ‎ 9 / 9‎