2009中考数学分类汇编-多边形的内角和以及平行四边形 17页

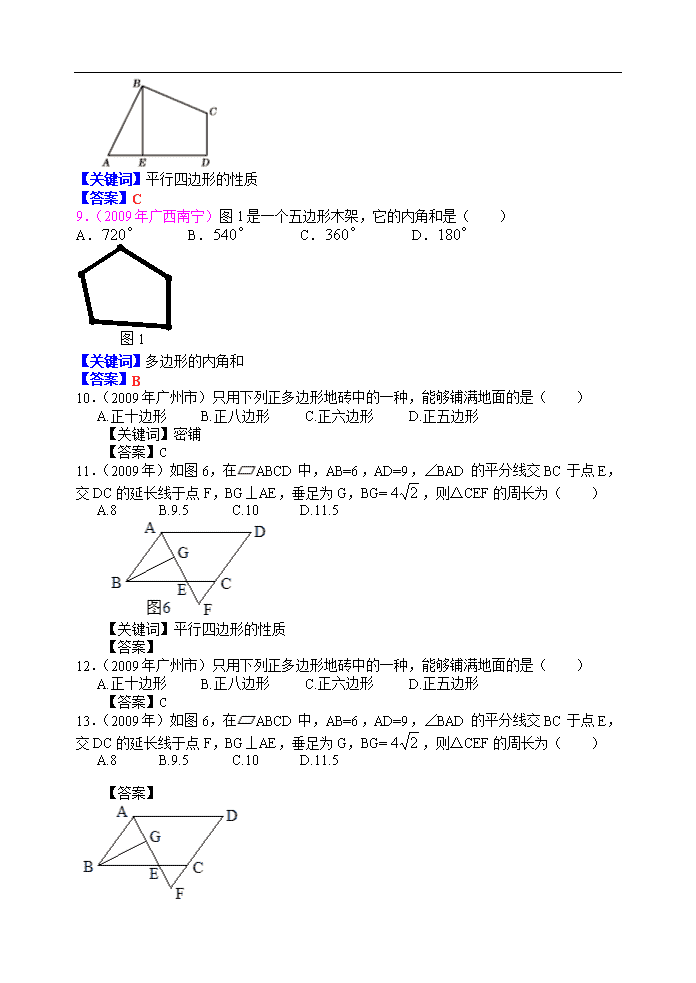
‎18．多边形内角和、平行四边形 一、选择题 ‎1．（2009东营）如图，在□ABCD中，已知AD＝8㎝， AB＝6㎝， DE平分∠ADC交BC边于点E，则BE等于（ ） ‎ A‎.‎‎2cm B‎.‎‎4cm C‎.‎‎6cm D‎.‎‎8cm A B C D E ‎【关键词】平行四边形 ‎【答案】A ‎2．（2009年桂林市、百色市）如图，□ABCD中，AC.BD为对角线，BC=6，‎ BC边上的高为4，则阴影部分的面积为（ ）．‎ ‎ A．3 B．‎6 C．12 D．24‎ ‎【关键词】平行四边形有关的计算 ‎【答案】C A D C B ‎3．（2009年常德市）下列命题中错误的是（　　）‎ A．两组对边分别相等的四边形是平行四边形 B．对角线相等的平行四边形是矩形 ‎ C．一组邻边相等的平行四边形是菱形 ‎ D．一组对边平行的四边形是梯形 ‎【关键词】平行四边形 ‎【答案】 D ‎4． (2009年黄冈市)5．一个多边形的内角和是外角和的2倍，则这个多边形的边数为（ ）‎ A．4 B．‎5 ‎ C．6 D．7‎ ‎【关键词】多边形的内角和 ‎【答案】A 提示：∠BAO+∠BCO=∠ABO+∠CBO=∠ABC=70°，所以∠BOA+∠BOC=360°－140°=220°，所以∠AOC=140°。‎ ‎5．（2009威海）如图，在四边形ABCD中，E是BC边的中点，连结DE并延长，交AB的延长线于F点，．添加一个条件，使四边形ABCD是平行四边形．你认为下面四个条件中可选择的是（　　）‎ A． B． ‎ C． D．‎ E B A F C D ‎【关键词】平行四边形的判定 ‎【答案】D ‎6．（2009年湖南长沙）如图，矩形的两条对角线相交于点，，则矩形的对角线的长是（ ）‎ A．2 B．‎4 ‎ C． D．‎ O D C A B 第14题 ‎【答案】B ‎【解析】本题考查了矩形的性质和等边三角形的判定。根据矩形的性质知：矩形的对角线相等且平分，所以AO=BO。在直角三角形AOB中，又有，所以三角形AOB为等边三角形，所以AO=AB=2，所以AC=2AO=4。‎ ‎7.（2009襄樊市）如图5，在中，于且是一元二次方程的根，则的周长为（ ）‎ A． B． C． D．‎ A D C EC B 图5‎ 解析：本题考查平行四边形及一元二次方程的有关知识，∵是一元二次方程的根，∴，∴AE=EB=EC=1，∴AB=，BC=2，∴的周长为，故选A。‎ ‎【关键词】一元二次方程的解法、平行四边形的性质 ‎【答案】A ‎8．（2009年甘肃白银）如图4，四边形ABCD中，AB=BC，∠ABC=∠CDA=90°，BE⊥AD于点E，且四边形ABCD的面积为8，则BE=（　　）‎ A．2 B．‎3 ‎ C． D．‎ ‎【关键词】平行四边形的性质 ‎【答案】C ‎9．（2009年广西南宁）图1是一个五边形木架，它的内角和是（ ）‎ A． B． C． D．‎ 图1‎ ‎【关键词】多边形的内角和 ‎【答案】B ‎10．（2009年广州市）只用下列正多边形地砖中的一种，能够铺满地面的是（ ）‎ A.正十边形 B.正八边形 C.正六边形 D.正五边形 ‎【关键词】密铺 ‎【答案】C ‎11．（2009年）如图6，在ABCD中，AB=6，AD=9，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE，垂足为G，BG=，则ΔCEF的周长为（ ）‎ A.8 B.‎9.5 C.10 D.11.5‎ ‎【关键词】平行四边形的性质 ‎【答案】‎ ‎12．（2009年广州市）只用下列正多边形地砖中的一种，能够铺满地面的是（ ）‎ A.正十边形 B.正八边形 C.正六边形 D.正五边形 ‎【答案】C ‎13．（2009年）如图6，在ABCD中，AB=6，AD=9，∠BAD的平分线交BC于点E，交DC的延长线于点F，BG⊥AE，垂足为G，BG=，则ΔCEF的周长为（ ）‎ A.8 B.‎9.5 C.10 D.11.5‎ ‎【答案】‎ ‎14．（2009年茂名市）5．已知一个多边形的内角和是540°，则这个多边形是（ ）‎ A．四边形 　　 B．五边形 C．六边形　 　　D．七边形 ‎【答案】‎ ‎15．（2009年茂名）6．杨伯家小院子的四棵小树刚好在其梯形院子各边的中点上，若在四边形种上小草，则这块草地的形状是（ ）‎ A．平行四边形　　　 　B．矩形 C．正方形　　　 D．菱形 Ａ Ｄ Ｈ Ｇ Ｃ Ｆ Ｂ Ｅ ‎【答案】‎ ‎16．（2009年新疆乌鲁木齐市）某多边形的内角和是其外角和的3倍，则此多边形的边数是（ ）．‎ A．5 B．‎6 ‎ C．7 D．8‎ ‎【答案】D ‎17．（2009年上海市)5．下列正多边形中，中心角等于内角的是（ ）‎ A．正六边形 B．正五边形 C．正四边形 C．正三边形 ‎【答案】C ‎18．（2009年黑龙江佳木斯）、如图，在平行四边形ABCD中，E为AD的中点，△DEF的面积为1，则△BCF的面积为 （ ）‎ A．1 B．2‎ C．3 D．4‎ ‎19. （2009年北京市）若一个正多边形的一个外角是40°，‎ 则这个正多边形的边数是 A.10 B‎.9 ‎ C.8 D.6‎ ‎【答案】B ‎20. （2009年北京市）若一个正多边形的一个外角是40°，‎ 则这个正多边形的边数是 A.10 B‎.9 ‎ C.8 D.6‎ ‎【答案】B 一、 填空题 ．（2009年甘肃庆阳）如图7，将正六边形绕其对称中心O旋转后，恰好能与原来的正六边形重合，那么旋转的角度至少是 度．‎ ‎【关键词】旋转；中心对称 ‎【答案】60 ‎ ‎2． (2009年牡丹江市)如图，□ABCD中，、分别为、边上的点，要使需添加一个条件： ．‎ A B C E D F ‎【关键词】平行四边形的性质 ‎【答案】‎ ‎3．（2009年广州市）已知命题“如果一个平行四边形的两条对角线互相垂直，那么这个平行四边形是菱形”，写出它的逆命题：________________________________‎ ‎【关键词】命题 ‎【答案】菱形的两条对角线互相垂直 ‎4．（2009年广西钦州）如图，在□ABCD中，∠A＝120°，则∠D＝_ _°.‎ ‎【关键词】平行四边形 ‎【答案】60‎ ‎5．（2009年哈尔滨）如图，在□ABCD中，BD为对角线，E、F分别是AD.BD的中点，连接EF．若EF＝3，则CD的长为 ． ‎ ‎【关键词】平行四边形有关的计算 ‎【答案】6. 因为EF是△ABD的中位线，则AB=6，又AB=CD，所以CD=6‎ ‎6．（2009年牡丹江）如图，中，、分别为、边上的点，要使需添加一个条件： ．‎ A B C E D F ‎【关键词】平行四边形的性质 ‎【答案】‎ ‎7．（2009年广州市）已知命题“如果一个平行四边形的两条对角线互相垂直，那么这个平行四边形是菱形”，写出它的逆命题：________________________________‎ ‎【答案】菱形的两条对角线互相垂直 ‎8．（09湖南怀化）亲爱的同学们，我们在教材中已经学习了:①等边三角形；②等腰梯形；③平行四边形；④等腰三角形；⑤圆．在以上五种几何图形中，既是轴对称图形， 又是中心对称图形的是 ．‎ ‎【关键词】对称性 ‎【答案】圆（或填⑤）‎ ‎10．（2009年山西省）如图，□ABCD的对角线、相交于点，点是的中点，的周长为‎16cm，则的周长是 cm．‎ A C D B E O ‎【答案】8‎ ‎9．（2009年郴州市）如图，在四边形中，已知，再添加一个条件___________（写出一个即可），则四边形是平行四边形．(图形中不再添加辅助线)‎ D C B A ‎【答案】‎ ‎10.（2009呼和浩特）如图，四边形中，，，，，则该四边形的面积是 ．‎ ‎【答案】‎ A B D C ‎．‎ 三、解答题 ‎1．（2009年湖南长沙）如图，是平行四边形对角线上两点，，求证：．‎ D C A B E F ‎【答案】证明：平行四边形中，，，‎ ‎ ．‎ 又，‎ ‎，‎ ‎，‎ ‎2．（2009柳州）如图6，四边形ABCD中，AB∥CD，∠B=∠D，，‎ 求四边形ABCD的周长．‎ ‎【‎ ‎【答案】20、‎ A D C B 解法一: ∵‎ ‎∴‎ 又∵‎ ‎∴ ‎ ‎∴∥即得是平行四边形 ‎ ‎∴ ‎ ‎∴四边形的周长 ‎ 解法二: ‎ A D C B 连接 ‎∵‎ ‎∴ ‎ 又∵‎ ‎∴≌‎ ‎∴ ‎ ‎∴四边形的周长 ‎ 解法三: ‎ A D C B 连接 ‎∵‎ ‎∴‎ 又∵ ‎ ‎∴‎ ‎∴∥即是平行四边形 ‎∴‎ ‎∴四边形的周长 ‎3.（2009年嘉兴市）在四边形ABCD中，∠D=60°，∠B比∠A大20°，∠C是∠A的2倍，求∠A，∠B，∠C的大小．‎ ‎【关键词】多边形的内角和 ‎【答案】设（度），则，．‎ 根据四边形内角和定理得，． ‎ 解得，．‎ ‎∴，，． ‎ ‎4．（2009年新疆）如图，是四边形的对角线上两点，．‎ 求证：（1）．‎ ‎（2）四边形是平行四边形．‎ A B D E F C ‎【关键词】平行四边形的性质,判定 ‎【答案】证明：（1），．，，．又，．‎ ‎（2）由（1）知，，．四边形是平行四边形（一组对边平行且相等的四边形是平行四边形）‎ ‎5．（2009年南宁市）25．如图13-1，在边长为5的正方形中，点、分别是、边上的点，且，.‎ ‎（1）求∶的值；‎ ‎（2）延长交正方形外角平分线（如图13-2），试判断 的大小关系，并说明理由；‎ ‎（3）在图13-2的边上是否存在一点，使得四边形是平行四边形？若存在，请给予证明；若不存在，请说明理由．‎ A D C B E B C E D A F P F ‎【关键词】平行四边形的判定 ‎【答案】解：（1）‎ 四边形ABCD为正方形 四边形是平行四边形． 解法：在边上存在一点，使四边形是平行四边形 证明：在边上取一点，使，连接、、．‎ 四边形为平行四边形 B C E D A F P ‎5‎ ‎4‎ ‎1‎ M ‎6．（2009年广州市）如图9，在ΔABC中，D、E、F分别为边AB、BC、CA的中点。‎ 证明：四边形DECF是平行四边形。‎ ‎【关键词】平行四边形的判定 ‎【答案】∵D.E、F分别为AB.BC.CA的中点，‎ ‎∴DF∥BC，DE∥AC，‎ ‎∴四边形DECF是平行四边形.‎ ‎7．（2009年包头）已知二次函数（）的图象经过点，，，直线（）与轴交于点．‎ ‎（1）求二次函数的解析式；‎ ‎（2）在直线（）上有一点（点在第四象限），使得为顶点的三角形与以为顶点的三角形相似，求点坐标（用含的代数式表示）；‎ ‎（3）在（2）成立的条件下，抛物线上是否存在一点，使得四边形为平行四边形？若存在，请求出的值及四边形的面积；若不存在，请说明理由．‎ y x O ‎【关键词】二次函数、相似三角形、运动变化、抛物线 解：（1）根据题意，得 y x O B A D C ‎(x=m)‎ ‎(F2)F1‎ E1 (E2)‎ 解得． ‎ ‎．‎ ‎（2）当时，‎ 得或，‎ ‎∵，‎ 当时，得，‎ ‎∴，‎ ‎∵点在第四象限，∴．‎ 当时，得，∴，‎ ‎∵点在第四象限，∴．‎ ‎（3）假设抛物线上存在一点，使得四边形为平行四边形，则 ‎，点的横坐标为，‎ 当点的坐标为时，点的坐标为，‎ ‎∵点在抛物线的图象上，‎ ‎∴，‎ ‎∴，‎ ‎∴，‎ ‎∴（舍去），‎ ‎∴，‎ ‎∴．‎ 当点的坐标为时，点的坐标为，‎ ‎∵点在抛物线的图象上，‎ ‎∴，‎ ‎∴，‎ ‎∴，∴（舍去），，‎ ‎∴，‎ ‎∴．‎ 注：各题的其它解法或证法可参照该评分标准给分．‎ ‎8．（2009年莆田）已知：如图在中，过对角线的中点作直线分别交的延长线、AB、DC、BC的延长线于点E、M、N、F。‎ ‎（1）观察图形并找出一对全等三角形：____________________，请加以证明；‎ E B M O D N F C A E B M O D N F C A ‎（2）在（1）中你所找出的一对全等三角形，其中一个三角形可由另一个三角形经过怎样的变换得到？‎ ‎【关键词】四边形、全等三角形、变换 ‎（1）；‎ 证明：∵四边形是平行四边形 ∴‎ ‎∴‎ 又∵‎ ‎∴‎ 证明：∵四边形是平行四边形 ∴‎ ‎∴‎ 又∵‎ ‎∴‎ ‎；‎ 证明：∵四边形是平行四边形 ∴‎ 又∵‎ ‎∴‎ ‎（2）绕点旋转后得到或以点为中心作对称变换得到． 8分 ‎9．(2009年温州)在所给的9×9方格中，每个小正方形的边长都是1．按要求画平行四边形，使它的四个顶点以及对角线交点都在方格的顶点上．‎ ‎(1)在图甲中画一个平行四边形，使它的周长是整数；(2)在图乙中画一个平行四边形，使它的周长不是整数．(注：图甲、图乙在答题纸上)‎ ‎【关键词】平行四边形的性质，判定 ‎【答案】解：（1）‎ ‎（2）‎ ‎10．（2009年中山）在中，，‎ 以为直径作，‎ ‎（1）求圆心到的距离（用含的代数式来表示）；‎ ‎（2）当取何值时，与相切．‎ A D B C O ‎【关键词】利用平行四边形证明线段相等 ‎【答案】（1）分别过两点作，垂足分别为点，点，‎ 就是圆心到的距离．‎ 四边形是平行四边形，‎ ‎．‎ A D B C O E F A D B C O E F 在中，，‎ ‎，‎ 圆心到CD的距离PF为．‎ ‎（2），‎ 为的直径，且，‎ 当时，与相切于点，‎ 即，‎ 当时，与相切．‎ ‎11．(2009年宁德市)（本题满分8分）如图：点A.D.B.E在同一直线上，AD=BE，AC=DF，AC∥DF，请从图中找出一个与∠E相等的角，并加以证明．（不再添加其他的字母与线段）‎ A F E D C B ‎【关键词】平行四边形的判定 ‎【答案】A F E D C B 解法1：图中∠CBA＝∠E ‎ 证明：∵AD＝BE ‎∴AD＋DB＝BE＋DB即AB＝DE ‎ ‎∵AC∥DF ∴∠A＝∠FDE ‎ 又∵AC＝DF ‎∴△ABC≌△DEF ‎ ‎∴∠CBA＝∠E ‎ A F E D C B 解法2：图中∠FCB＝∠E ‎ 证明：∵AC＝DF，AC∥DF ‎∴四边形ADFC是平行四边形 ‎ ‎ ∴CF∥AD，CF＝AD ‎ ‎∵AD＝BE ∴CF＝BE，CF∥BE ‎ ‎∴四边形BEFC是平行四边形 ‎ ‎∴∠FCB＝∠E ‎ ‎12．（2009年山东青岛市）如图，在梯形ABCD中，，，，，点由B出发沿BD方向匀速运动，速度为‎1cm/s；同时，线段EF由DC出发沿DA方向匀速运动，速度为‎1cm/s，交于Q，连接PE．若设运动时间为（s）（）．解答下列问题：‎ ‎（1）当为何值时，？‎ ‎（2）设的面积为（cm2），求与之间的函数关系式；‎ ‎（3）是否存在某一时刻，使？若存在，求出此时的值；若不存在，说明理由．‎ ‎（4）连接，在上述运动过程中，五边形的面积是否发生变化？说明理由．‎ A E D Q P B F C ‎【关键词】全等三角形的性质与判定、相似三角形判定和性质、平行四边形有关的计算 ‎【答案】‎ A E D Q P B F C N M 解：（1）∵‎ ‎∴．‎ 而，‎ ‎∴，‎ ‎∴．‎ ‎∴当．‎ ‎（2）∵平行且等于，‎ ‎∴四边形是平行四边形．‎ ‎∴．‎ ‎∵，‎ ‎∴．‎ ‎∴．‎ ‎∴．‎ ‎．‎ ‎∴．‎ 过B作，交于，过作，交于．‎ ‎．‎ ‎∵，‎ ‎∴．‎ 又，‎ ‎，‎ ‎，‎ ‎．‎ ‎（3）．‎ 若，‎ 则有，‎ 解得．‎ ‎（4）在和中，‎ ‎∴‎ ‎ ‎ ‎ ．‎ ‎∴在运动过程中，五边形的面积不变．‎ ‎13． (2009年达州)如图10，⊙O的弦AD∥BC,过点D的切线交BC的延长线于点E，AC∥DE交BD于点H，DO及延长线分别交AC.BC于点G、F.‎ ‎(1)求证：DF垂直平分AC；‎ ‎（2）求证：FC＝CE；‎ ‎（3）若弦AD＝5㎝，AC＝8㎝，求⊙O的半径. ‎ ‎【关键词】圆,平行四边形,勾股定理 ‎【答案】‎ ‎（1）∵DE是⊙O的切线，且DF过圆心O ‎∴DF⊥DE 又∵AC∥DE ‎∴DF⊥AC ‎∴DF垂直平分AC ‎ ‎（2）由（1）知：AG=GC 又∵AD∥BC ‎∴∠DAG=∠FCG 又∵∠AGD=∠CGF ‎∴△AGD≌△CGF（ASA）‎ ‎∴AD=FC ‎∵AD∥BC且AC∥DE ‎∴四边形ACED是平行四边形 ‎∴AD=CE ‎∴FC=CE5分 ‎（3）连结AO； ∵AG=GC，AC=‎8cm，∴AG=‎‎4cm 在Rt△AGD中，由勾股定理得 GD=AD2-AG2=52-42=‎3cm ‎ 设圆的半径为r，则AO=r，OG=r-3‎ 在Rt△AOG中，由勾股定理得 AO2=OG2+AG2‎ 有：r2=(r-3)2+42解得 r=256 ‎ ‎∴⊙O的半径为‎256cm.‎