2019年四川省宜宾市中考数学试卷含答案 27页

‎2019年四川省宜宾市中考数学试卷 一、选择题:(本大题共8小题,每小题3分,共24分)在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项填涂在答题卡对应题目上。‎ ‎1．（3分）2的倒数是（　　）‎ A．‎1‎‎2‎ B．﹣2 C．‎-‎‎1‎‎2‎ D．‎‎±‎‎1‎‎2‎ ‎2．（3分）人体中枢神经系统中约含有1千亿个神经元，某种神经元的直径约为52微米，52微米为0.000052米．将0.000052用科学记数法表示为（　　）‎ A．5.2×10﹣6 B．5.2×10﹣5 C．52×10﹣6 D．52×10﹣5‎ ‎3．（3分）如图，四边形ABCD是边长为5的正方形，E是DC上一点，DE＝1，将△ADE绕着点A顺时针旋转到与△ABF重合，则EF＝（　　）‎ A．‎41‎ B．‎42‎ C．5‎2‎ D．2‎‎13‎ ‎4．（3分）一元二次方程x2﹣2x+b＝0的两根分别为x1和x2，则x1+x2为（　　）‎ A．﹣2 B．b C．2 D．﹣b ‎5．（3分）已知一个组合体是由几个相同的正方体叠合在一起组成，该组合体的主视图与俯视图如图所示，则该组合体中正方体的个数最多是（　　）‎ A．10 B．9 C．8 D．7‎ ‎6．（3分）如表记录了两位射击运动员的八次训练成绩：‎ 次数 环数 运动员 第1次 第2次 第3次 第4次 第5次 第6次 第7次 第8次 甲 ‎10‎ ‎7‎ ‎7‎ ‎8‎ ‎8‎ ‎8‎ ‎9‎ ‎7‎ 乙 ‎10‎ ‎5‎ ‎5‎ ‎8‎ ‎9‎ ‎9‎ ‎8‎ ‎10‎ 根据以上数据，设甲、乙的平均数分别为x甲、x乙，甲、乙的方差分别为s甲2，s乙2，则下列结论正确的是（　　）‎ A．x甲‎=‎x乙，s甲2＜s乙2 B．x甲‎=‎x乙，s甲2＞s乙2 ‎ C．x甲‎＞‎x乙，s甲2＜s乙2 D．x甲‎＜‎x乙，s甲2＜s乙2‎ ‎7．（3分）如图，∠EOF的顶点O是边长为2的等边△ABC的重心，∠EOF的两边与△ABC的边交于E，F，∠EOF＝120°，则∠EOF与△ABC的边所围成阴影部分的面积是（　　）‎ A．‎3‎‎2‎ B．‎2‎‎3‎‎5‎ C．‎3‎‎3‎ D．‎‎3‎‎4‎ ‎8．（3分）已知抛物线y＝x2﹣1与y轴交于点A，与直线y＝kx（k为任意实数）相交于B，C两点，则下列结论不正确的是（　　）‎ A．存在实数k，使得△ABC为等腰三角形 ‎ B．存在实数k，使得△ABC的内角中有两角分别为30°和60° ‎ C．任意实数k，使得△ABC都为直角三角形 ‎ D．存在实数k，使得△ABC为等边三角形 二、填空题:(本大题共8小题,每小题3分,共24分)请把答案直接填在答题卡对应题中横上。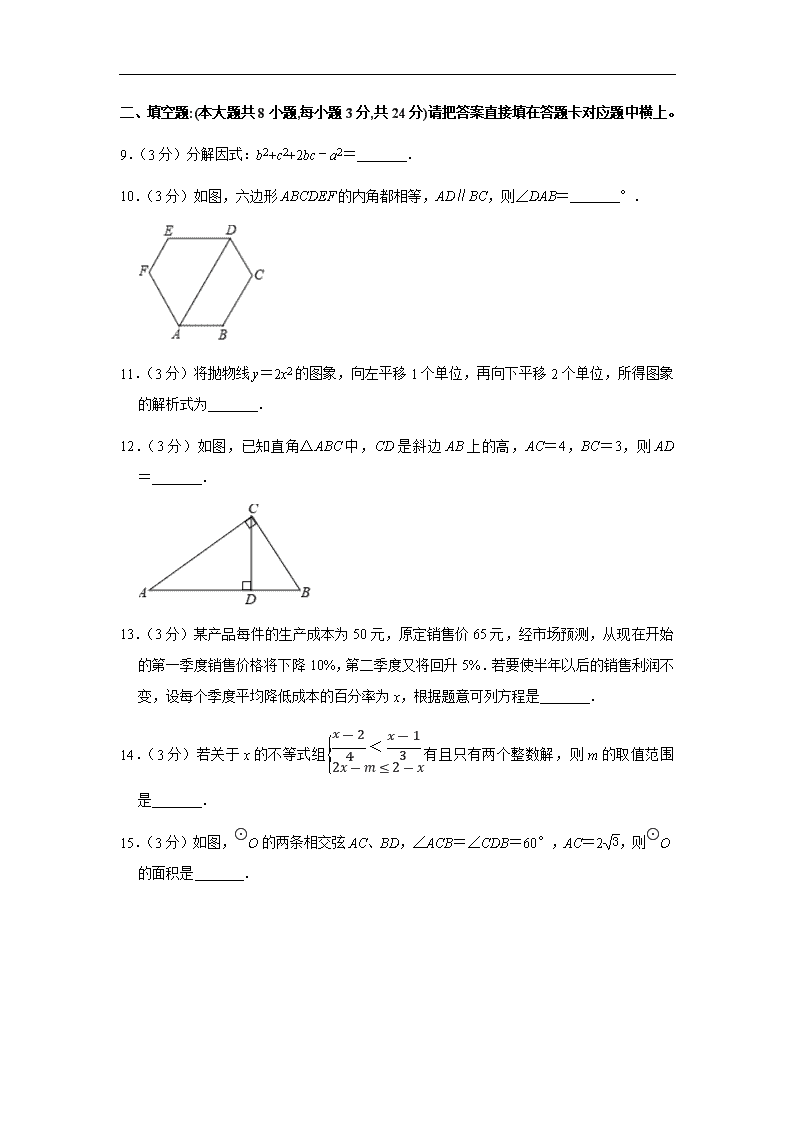‎ ‎9．（3分）分解因式：b2+c2+2bc﹣a2＝　 　．‎ ‎10．（3分）如图，六边形ABCDEF的内角都相等，AD∥BC，则∠DAB＝　 　°．‎ ‎11．（3分）将抛物线y＝2x2的图象，向左平移1个单位，再向下平移2个单位，所得图象的解析式为　 　．‎ ‎12．（3分）如图，已知直角△ABC中，CD是斜边AB上的高，AC＝4，BC＝3，则AD＝　 　．‎ ‎13．（3分）某产品每件的生产成本为50元，原定销售价65元，经市场预测，从现在开始的第一季度销售价格将下降10%，第二季度又将回升5%．若要使半年以后的销售利润不变，设每个季度平均降低成本的百分率为x，根据题意可列方程是　 　．‎ ‎14．（3分）若关于x的不等式组x-2‎‎4‎‎＜‎x-1‎‎3‎‎2x-m≤2-x有且只有两个整数解，则m的取值范围是　 　．‎ ‎15．（3分）如图，⊙O的两条相交弦AC、BD，∠ACB＝∠CDB＝60°，AC＝2‎3‎，则⊙O的面积是　 　．‎ ‎16．（3分）如图，△ABC和△CDE都是等边三角形，且点A、C、E在同一直线上，AD与BE、BC分别交于点F、M，BE与CD交于点N．下列结论正确的是　 　（写出所有正确结论的序号）．‎ ‎①AM＝BN；②△ABF≌△DNF；③∠FMC+∠FNC＝180°；④‎‎1‎MN‎=‎1‎AC+‎‎1‎CE 三、解答题:(本大题共8小题,共72分)解答应写出文字说明、证明过程或演算步骤。‎ ‎17．（10分）（1）计算：（2019‎-‎‎2‎）0﹣2﹣1+|﹣1|+sin245°‎ ‎（2）化简：‎2xyx‎2‎‎-‎y‎2‎‎÷‎（‎1‎x-y‎+‎‎1‎x+y）‎ ‎18．（6分）如图，AB＝AD，AC＝AE，∠BAE＝∠DAC．求证：∠C＝∠E．‎ ‎19．（8分）某校在七、八、九三个年级中进行“一带一路”知识竞赛，分别设有一等奖、二等奖、三等奖、优秀奖、纪念奖．现对三个年级同学的获奖情况进行了统计，其中获得纪念奖有17人，获得三等奖有10人，并制作了如图不完整的统计图．‎ ‎（1）求三个年级获奖总人数；‎ ‎（2）请补全扇形统计图的数据；‎ ‎（3）在获一等奖的同学中，七年级和八年级的人数各占‎1‎‎4‎，其余为九年级的同学，现从获一等奖的同学中选2名参加市级比赛，通过列表或者树状图的方法，求所选出的2人中既有七年级又有九年级同学的概率．‎ ‎20．（8分）甲、乙两辆货车分别从A、B两城同时沿高速公路向C城运送货物．已知A、C两城相距450千米，B、C两城的路程为440千米，甲车比乙车的速度快10千米/小时，甲车比乙车早半小时到达C城．求两车的速度．‎ ‎21．（8分）如图，为了测得某建筑物的高度AB，在C处用高为1米的测角仪CF，测得该建筑物顶端A的仰角为45°，再向建筑物方向前进40米，又测得该建筑物顶端A的仰角为60°．求该建筑物的高度AB．（结果保留根号）‎ ‎22．（10分）如图，已知反比例函数y‎=‎kx（k＞0）的图象和一次函数y＝﹣x+b的图象都过点P（1，m），过点P作y轴的垂线，垂足为A，O为坐标原点，△OAP的面积为1．‎ ‎（1）求反比例函数和一次函数的解析式；‎ ‎（2）设反比例函数图象与一次函数图象的另一交点为M，过M作x轴的垂线，垂足为B，求五边形OAPMB的面积．‎ ‎23．（10分）如图，线段AB经过⊙O的圆心O，交⊙O于A、C两点，BC＝1，AD为⊙O的弦，连结BD，∠BAD＝∠ABD＝30°，连结DO并延长交⊙O于点E，连结BE交⊙O于点M．‎ ‎（1）求证：直线BD是⊙O的切线；‎ ‎（2）求⊙O的半径OD的长；‎ ‎（3）求线段BM的长．‎ ‎24．（12分）如图，在平面直角坐标系xOy中，已知抛物线y＝ax2﹣2x+c与直线y＝kx+b都经过A（0，﹣3）、B（3，0）两点，该抛物线的顶点为C．‎ ‎（1）求此抛物线和直线AB的解析式；‎ ‎（2）设直线AB与该抛物线的对称轴交于点E，在射线EB上是否存在一点M，过M作x轴的垂线交抛物线于点N，使点M、N、C、E是平行四边形的四个顶点？若存在，求点M的坐标；若不存在，请说明理由；‎ ‎（3）设点P是直线AB下方抛物线上的一动点，当△PAB面积最大时，求点P的坐标，并求△PAB面积的最大值．‎ ‎2019年四川省宜宾市中考数学试卷 参考答案与试题解析 一、选择题:(本大题共8小题,每小题3分,共24分)在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项填涂在答题卡对应题目上。‎ ‎1．（3分）2的倒数是（　　）‎ A．‎1‎‎2‎ B．﹣2 C．‎-‎‎1‎‎2‎ D．‎‎±‎‎1‎‎2‎ ‎【解答】解：2的倒数是‎1‎‎2‎，‎ 故选：A．‎ ‎2．（3分）人体中枢神经系统中约含有1千亿个神经元，某种神经元的直径约为52微米，52微米为0.000052米．将0.000052用科学记数法表示为（　　）‎ A．5.2×10﹣6 B．5.2×10﹣5 C．52×10﹣6 D．52×10﹣5‎ ‎【解答】解：0.000052＝5.2×10﹣5；‎ 故选：B．‎ ‎3．（3分）如图，四边形ABCD是边长为5的正方形，E是DC上一点，DE＝1，将△ADE绕着点A顺时针旋转到与△ABF重合，则EF＝（　　）‎ A．‎41‎ B．‎42‎ C．5‎2‎ D．2‎‎13‎ ‎【解答】解：由旋转变换的性质可知，△ADE≌△ABF，‎ ‎∴正方形ABCD的面积＝四边形AECF的面积＝25，‎ ‎∴BC＝5，BF＝DE＝1，‎ ‎∴FC＝6，CE＝4，‎ ‎∴EF‎=FC‎2‎+CE‎2‎=‎52‎=‎2‎13‎．‎ 故选：D．‎ ‎4．（3分）一元二次方程x2﹣2x+b＝0的两根分别为x1和x2，则x1+x2为（　　）‎ A．﹣2 B．b C．2 D．﹣b ‎【解答】解：根据题意得：‎ x1+x2‎=-‎-2‎‎1‎=‎2，‎ 故选：C．‎ ‎5．（3分）已知一个组合体是由几个相同的正方体叠合在一起组成，该组合体的主视图与俯视图如图所示，则该组合体中正方体的个数最多是（　　）‎ A．10 B．9 C．8 D．7‎ ‎【解答】解：从俯视图可得最底层有5个小正方体，由主视图可得上面一层是2个，3个或4个小正方体，‎ 则组成这个几何体的小正方体的个数是7个或8个或9个，‎ 组成这个几何体的小正方体的个数最多是9个．‎ 故选：B．‎ ‎6．（3分）如表记录了两位射击运动员的八次训练成绩：‎ 次数 环数 第1次 第2次 第3次 第4次 第5次 第6次 第7次 第8次 运动员 甲 ‎10‎ ‎7‎ ‎7‎ ‎8‎ ‎8‎ ‎8‎ ‎9‎ ‎7‎ 乙 ‎10‎ ‎5‎ ‎5‎ ‎8‎ ‎9‎ ‎9‎ ‎8‎ ‎10‎ 根据以上数据，设甲、乙的平均数分别为x甲、x乙，甲、乙的方差分别为s甲2，s乙2，则下列结论正确的是（　　）‎ A．x甲‎=‎x乙，s甲2＜s乙2 B．x甲‎=‎x乙，s甲2＞s乙2 ‎ C．x甲‎＞‎x乙，s甲2＜s乙2 D．x甲‎＜‎x乙，s甲2＜s乙2‎ ‎【解答】解：（1）x甲‎=‎‎1‎‎8‎（10+7+7+8+8+8+9+7）＝8；x乙‎=‎‎1‎‎8‎（10+5+5+8+9+9+8+10）＝8；‎ s甲2‎=‎‎1‎‎8‎[（10﹣8）2+（7﹣8）2+（7﹣8）2+（8﹣8）2+（8﹣8）2+（8﹣8）2+（9﹣8）2+（7﹣8）2]＝1；‎ s乙2‎=‎‎1‎‎8‎[（10﹣8）2+（5﹣8）2+（5﹣8）2+（8﹣8）2+（9﹣8）2+（9﹣8）2+（8﹣8）2+（10﹣8）2]‎=‎‎7‎‎2‎，‎ ‎∴x甲‎=‎x乙，s甲2＜s乙2，‎ 故选：A．‎ ‎7．（3分）如图，∠EOF的顶点O是边长为2的等边△ABC的重心，∠EOF的两边与△ABC的边交于E，F，∠EOF＝120°，则∠EOF与△ABC的边所围成阴影部分的面积是（　　）‎ A．‎3‎‎2‎ B．‎2‎‎3‎‎5‎ C．‎3‎‎3‎ D．‎‎3‎‎4‎ ‎【解答】解：连接OB、OC，过点O作ON⊥BC，垂足为N，‎ ‎∵△ABC为等边三角形，‎ ‎∴∠ABC＝∠ACB＝60°，‎ ‎∵点O为△ABC的内心 ‎∴∠OBC＝∠OBA‎=‎‎1‎‎2‎∠ABC，∠OCB‎=‎‎1‎‎2‎∠ACB．‎ ‎∴∠OBA＝∠OBC＝∠OCB＝30°．‎ ‎∴OB＝OC．∠BOC＝120°，‎ ‎∵ON⊥BC，BC＝2，‎ ‎∴BN＝NC＝1，‎ ‎∴ON＝tan∠OBC•BN‎=‎3‎‎3‎×‎1‎=‎‎3‎‎3‎，‎ ‎∴S△OBC‎=‎‎1‎‎2‎BC•ON‎=‎‎3‎‎3‎．‎ ‎∵∠EOF＝∠AOB＝120°，‎ ‎∴∠EOF﹣∠BOF＝∠AOB﹣∠BOF，即∠EOB＝∠FOC．‎ 在△EOB和△FOC中，‎ ‎∠OBE=∠OCF=30°‎OB=OC‎∠EOB=∠FOC‎，‎ ‎∴△EOB≌△FOC（ASA）．‎ ‎∴S阴影＝S△OBC‎=‎‎3‎‎3‎ 故选：C．‎ ‎8．（3分）已知抛物线y＝x2﹣1与y轴交于点A，与直线y＝kx（k为任意实数）相交于B，C两点，则下列结论不正确的是（　　）‎ A．存在实数k，使得△ABC为等腰三角形 ‎ B．存在实数k，使得△ABC的内角中有两角分别为30°和60° ‎ C．任意实数k，使得△ABC都为直角三角形 ‎ D．存在实数k，使得△ABC为等边三角形 ‎【解答】解：A、如图1，可以得△ABC为等腰三角形，正确；‎ B、如图3，∠ACB＝30°，∠ABC＝60°，可以得△ABC的内角中有两角分别为30°和60°，正确；‎ C、如图2和3，∠BAC＝90°，可以得△ABC为直角三角形，正确；‎ D、不存在实数k，使得△ABC为等边三角形，不正确；‎ 本题选择结论不正确的，‎ 故选：D．‎ 二、填空题:(本大题共8小题,每小题3分,共24分)请把答案直接填在答题卡对应题中横上。‎ ‎9．（3分）分解因式：b2+c2+2bc﹣a2＝　（b+c+a）（b+c﹣a）　．‎ ‎【解答】解：原式＝（b+c）2﹣a2＝（b+c+a）（b+c﹣a）．‎ 故答案为：（b+c+a）（b+c﹣a）‎ ‎10．（3分）如图，六边形ABCDEF的内角都相等，AD∥BC，则∠DAB＝　60　°．‎ ‎【解答】解：在六边形ABCDEF中，‎ ‎（6﹣2）×180°＝720°，‎ ‎720°‎‎6‎‎=‎‎120°，‎ ‎∴∠B＝120°，‎ ‎∵AD∥BC，‎ ‎∴∠DAB＝180°﹣∠B＝60°，‎ 故答案为：60°．‎ ‎11．（3分）将抛物线y＝2x2的图象，向左平移1个单位，再向下平移2个单位，所得图象的解析式为　y＝2（x+1）2﹣2　．‎ ‎【解答】解：将抛物线y＝2x2的图象，向左平移1个单位，再向下平移2个单位，‎ 所得图象的解析式为：y＝2（x+1）2﹣2．‎ 故答案为：y＝2（x+1）2﹣2．‎ ‎12．（3分）如图，已知直角△ABC中，CD是斜边AB上的高，AC＝4，BC＝3，则AD＝　‎16‎‎5‎　．‎ ‎【解答】解：在Rt△ABC中，AB‎=AC‎2‎+BC‎2‎=‎5，‎ 由射影定理得，AC2＝AD•AB，‎ ‎∴AD‎=AC‎2‎AB=‎‎16‎‎5‎，‎ 故答案为：‎16‎‎5‎．‎ ‎13．（3分）某产品每件的生产成本为50元，原定销售价65元，经市场预测，从现在开始的第一季度销售价格将下降10%，第二季度又将回升5%．若要使半年以后的销售利润不变，设每个季度平均降低成本的百分率为x，根据题意可列方程是　65×（1﹣10%）×（1+5%）﹣50（1﹣x）2＝65﹣50　．‎ ‎【解答】解：设每个季度平均降低成本的百分率为x，‎ 依题意，得：65×（1﹣10%）×（1+5%）﹣50（1﹣x）2＝65﹣50．‎ 故答案为：65×（1﹣10%）×（1+5%）﹣50（1﹣x）2＝65﹣50．‎ ‎14．（3分）若关于x的不等式组x-2‎‎4‎‎＜‎x-1‎‎3‎‎2x-m≤2-x有且只有两个整数解，则m的取值范围是　﹣2≤m＜1　．‎ ‎【解答】解：‎x-2‎‎4‎‎＜x-1‎‎3‎①‎‎2x-m≤2-x②‎ 解不等式①得：x＞﹣2，‎ 解不等式②得：x‎≤‎m+2‎‎3‎，‎ ‎∴不等式组的解集为﹣2＜x‎≤‎m+2‎‎3‎，‎ ‎∵不等式组只有两个整数解，‎ ‎∴0‎≤m+2‎‎3‎＜‎1，‎ 解得：﹣2≤m＜1，‎ 故答案为﹣2≤m＜1．‎ ‎15．（3分）如图，⊙O的两条相交弦AC、BD，∠ACB＝∠CDB＝60°，AC＝2‎3‎，则⊙O的面积是　4π　．‎ ‎【解答】解：∵∠A＝∠BDC，‎ 而∠ACB＝∠CDB＝60°，‎ ‎∴∠A＝∠ACB＝60°，‎ ‎∴△ACB为等边三角形，‎ ‎∵AC＝2‎3‎，‎ ‎∴圆的半径为2，‎ ‎∴⊙O的面积是4π，‎ 故答案为：4π．‎ ‎16．（3分）如图，△ABC和△CDE都是等边三角形，且点A、C、E在同一直线上，AD与BE、BC分别交于点F、M，BE与CD交于点N．下列结论正确的是　①③④　（写出所有正确结论的序号）．‎ ‎①AM＝BN；②△ABF≌△DNF；③∠FMC+∠FNC＝180°；④‎‎1‎MN‎=‎1‎AC+‎‎1‎CE ‎【解答】证明：①∵△ABC和△CDE都是等边三角形，‎ ‎∴AC＝BC，CE＝CD，∠ACB＝∠ECD＝60°，‎ ‎∴∠ACB+∠ACE＝∠ECD+∠ACE，‎ 即∠BCE＝∠ACD，‎ 在△BCE和△ACD中，‎ BC=AC‎∠BCE=∠ACDCE=CD‎，‎ ‎∴△BCE≌△ACD（SAS），‎ ‎∴AD＝BE，∠ADC＝∠BEC，∠CAD＝∠CBE，‎ 在△DMC和△ENC中，‎ ‎∠MDC=∠NECDC=BC‎∠MCD=∠NCE=60°‎‎，‎ ‎∴△DMC≌△ENC（ASA），‎ ‎∴DM＝EN，CM＝CN，‎ ‎∴AD﹣DM＝BE﹣EN，即AM＝BN；‎ ‎②∵∠ABC＝60°＝∠BCD，‎ ‎∴AB∥CD，‎ ‎∴∠BAF＝∠CDF，‎ ‎∵∠AFB＝∠DFN，‎ ‎∴△ABF∽△DNF，找不出全等的条件；‎ ‎③∵∠AFB+∠ABF+∠BAF＝180°，∠FBC＝∠CAF，‎ ‎∴∠AFB+∠ABC+∠BAC＝180°，‎ ‎∴∠AFB＝60°，‎ ‎∴∠MFN＝120°，‎ ‎∵∠MCN＝60°，‎ ‎∴∠FMC+∠FNC＝180°；‎ ‎④∵CM＝CN，∠MCN＝60°，‎ ‎∴△MCN是等边三角形，‎ ‎∴∠MNC＝60°，‎ ‎∵∠DCE＝60°，‎ ‎∴MN∥AE，‎ ‎∴MNAC‎=DNCD=‎CD-CNCD，‎ ‎∵CD＝CE，MN＝CN，‎ ‎∴MNAC‎=‎CE-MNCE，‎ ‎∴MNAC‎=‎1‎-‎MNCE，‎ 两边同时除MN得‎1‎AC‎=‎1‎MN-‎‎1‎CE，‎ ‎∴‎1‎MN‎=‎1‎AC+‎‎1‎CE．‎ 故答案为①③④‎ 三、解答题:(本大题共8小题,共72分)解答应写出文字说明、证明过程或演算步骤。‎ ‎17．（10分）（1）计算：（2019‎-‎‎2‎）0﹣2﹣1+|﹣1|+sin245°‎ ‎（2）化简：‎2xyx‎2‎‎-‎y‎2‎‎÷‎（‎1‎x-y‎+‎‎1‎x+y）‎ ‎【解答】解：（1）原式＝1‎-‎1‎‎2‎+‎1+（‎2‎‎2‎）2‎ ‎＝2‎‎-‎1‎‎2‎+‎‎1‎‎2‎ ‎＝2‎ ‎（2）原式‎=‎2xy‎(x+y)(x-y)‎÷‎‎2x‎(x+y)(x-y)‎ ‎=‎2xy‎(x+y)(x-y)‎×‎‎(x+y)(x-y)‎‎2x‎ ‎ ‎＝y．‎ ‎18．（6分）如图，AB＝AD，AC＝AE，∠BAE＝∠DAC．求证：∠C＝∠E．‎ ‎【解答】证明：∵∠BAE＝∠DAC ‎∴∠BAE+∠CAE＝∠DAC+∠CAE ‎∴∠CAB＝∠EAD，且AB＝AD，AC＝AE ‎∴△ABC≌△ADE（SAS）‎ ‎∴∠C＝∠E ‎19．（8分）某校在七、八、九三个年级中进行“一带一路”知识竞赛，分别设有一等奖、二等奖、三等奖、优秀奖、纪念奖．现对三个年级同学的获奖情况进行了统计，其中获得纪念奖有17人，获得三等奖有10人，并制作了如图不完整的统计图．‎ ‎（1）求三个年级获奖总人数；‎ ‎（2）请补全扇形统计图的数据；‎ ‎（3）在获一等奖的同学中，七年级和八年级的人数各占‎1‎‎4‎，其余为九年级的同学，现从获一等奖的同学中选2名参加市级比赛，通过列表或者树状图的方法，求所选出的2人中既有七年级又有九年级同学的概率．‎ ‎【解答】解：（1）三个年级获奖总人数为17÷34%＝50（人）；‎ ‎（2）三等奖对应的百分比为‎10‎‎50‎‎×‎100%＝20%，‎ 则一等奖的百分比为1﹣（14%+20%+34%+24%）＝8%，‎ 补全图形如下：‎ ‎（3）由题意知，获一等奖的学生中，七年级有1人，八年级有1人，九年级有2人，‎ 画树状图为：（用A、B、C分别表示七年级、八年级和九年级的学生）‎ 共有12种等可能的结果数，其中所选出的两人中既有七年级又有九年级同学的结果数为4，‎ 所以所选出的两人中既有七年级又有九年级同学的概率为‎1‎‎3‎．‎ ‎20．（8分）甲、乙两辆货车分别从A、B两城同时沿高速公路向C城运送货物．已知A、C两城相距450千米，B、C两城的路程为440千米，甲车比乙车的速度快10千米/小时，甲车比乙车早半小时到达C城．求两车的速度．‎ ‎【解答】解：设乙车的速度为x千米/时，则甲车的速度为（x+10）千米/时．‎ 根据题意，得：‎450‎x+10‎‎+‎1‎‎2‎=‎‎440‎x，‎ 解得：x＝80，或x＝﹣110（舍去），‎ ‎∴x＝80，‎ 经检验，x＝，80是原方程的解，且符合题意．‎ 当x＝80时，x+10＝90．‎ 答：甲车的速度为90千米/时，乙车的速度为80千米/时．‎ ‎21．（8分）如图，为了测得某建筑物的高度AB，在C处用高为1米的测角仪CF，测得该建筑物顶端A的仰角为45°，再向建筑物方向前进40米，又测得该建筑物顶端A的仰角为60°．求该建筑物的高度AB．（结果保留根号）‎ ‎【解答】解：设AM＝x米，‎ 在Rt△AFM中，∠AFM＝45°，‎ ‎∴FM＝AM＝x，‎ 在Rt△AEM中，tan∠AEM‎=‎AMEM，‎ 则EM‎=AMtan∠AEM=‎‎3‎‎3‎x，‎ 由题意得，FM﹣EM＝EF，即x‎-‎‎3‎‎3‎x＝40，‎ 解得，x＝60+20‎3‎，‎ ‎∴AB＝AM+MB＝61+20‎3‎，‎ 答：该建筑物的高度AB为（61+20‎3‎）米．‎ ‎22．（10分）如图，已知反比例函数y‎=‎kx（k＞0）的图象和一次函数y＝﹣x+b的图象都过点P（1，m），过点P作y轴的垂线，垂足为A，O为坐标原点，△OAP的面积为1．‎ ‎（1）求反比例函数和一次函数的解析式；‎ ‎（2）设反比例函数图象与一次函数图象的另一交点为M，过M作x轴的垂线，垂足为B，求五边形OAPMB的面积．‎ ‎【解答】解：（1）∵过点P作y轴的垂线，垂足为A，O为坐标原点，△OAP的面积为1．‎ ‎∴S△OPA‎=‎‎1‎‎2‎|k|＝1，‎ ‎∴|k|＝2，‎ ‎∵在第一象限，‎ ‎∴k＝2，‎ ‎∴反比例函数的解析式为y‎=‎‎2‎x；‎ ‎∵反比例函数y‎=‎kx（k＞0）的图象过点P（1，m），‎ ‎∴m‎=‎2‎‎1‎=‎2，‎ ‎∴P（1，2），‎ ‎∵次函数y＝﹣x+b的图象过点P（1，2），‎ ‎∴2＝﹣1+b，解得b＝3，‎ ‎∴一次函数的解析式为y＝﹣x+3；‎ ‎（2）设直线y＝﹣x+3交x轴、y轴于C、D两点，‎ ‎∴C（3，0），D（0，3），‎ 解y=-x+3‎y=‎‎2‎x得x=1‎y=2‎或x=2‎y=1‎，‎ ‎∴P（1，2），M（2，1），‎ ‎∴PA＝1，AD＝3﹣2＝1，BM＝1，BC＝3﹣2＝1，‎ ‎∴五边形OAPMB的面积为：S△COD﹣S△BCM﹣S△ADP‎=‎1‎‎2‎×‎3×3‎-‎1‎‎2‎×‎1×1‎-‎1‎‎2‎×‎1×1‎=‎‎7‎‎2‎．‎ ‎23．（10分）如图，线段AB经过⊙O的圆心O，交⊙O于A、C两点，BC＝1，AD为⊙O的弦，连结BD，∠BAD＝∠ABD＝30°，连结DO并延长交⊙O于点E，连结BE交⊙O于点M．‎ ‎（1）求证：直线BD是⊙O的切线；‎ ‎（2）求⊙O的半径OD的长；‎ ‎（3）求线段BM的长．‎ ‎【解答】（1）证明：∵OA＝OD，∠A＝∠B＝30°，‎ ‎∴∠A＝∠ADO＝30°，‎ ‎∴∠DOB＝∠A+∠ADO＝60°，‎ ‎∴∠ODB＝180°﹣∠DOB﹣∠B＝90°，‎ ‎∵OD是半径，‎ ‎∴BD是⊙O的切线；‎ ‎（2）∵∠ODB＝90°，∠DBC＝30°，‎ ‎∴OD‎=‎‎1‎‎2‎OB，‎ ‎∵OC＝OD，‎ ‎∴BC＝OC＝1，‎ ‎∴⊙O的半径OD的长为1；‎ ‎（3）∵OD＝1，‎ ‎∴DE＝2，BD‎=‎‎3‎，‎ ‎∴BE‎=BD‎2‎+DE‎2‎=‎‎7‎，‎ ‎∵BD是⊙O的切线，BE是⊙O 的割线，‎ ‎∴BD2＝BM•BE，‎ ‎∴BM‎=BD‎2‎BE=‎3‎‎7‎=‎‎3‎‎7‎‎7‎．‎ ‎24．（12分）如图，在平面直角坐标系xOy中，已知抛物线y＝ax2﹣2x+c与直线y＝kx+b都经过A（0，﹣3）、B（3，0）两点，该抛物线的顶点为C．‎ ‎（1）求此抛物线和直线AB的解析式；‎ ‎（2）设直线AB与该抛物线的对称轴交于点E，在射线EB上是否存在一点M，过M作x轴的垂线交抛物线于点N，使点M、N、C、E是平行四边形的四个顶点？若存在，求点M的坐标；若不存在，请说明理由；‎ ‎（3）设点P是直线AB下方抛物线上的一动点，当△PAB面积最大时，求点P的坐标，并求△PAB面积的最大值．‎ ‎【解答】解：（1）∵抛物线y＝ax2﹣2x+c经过A（0，﹣3）、B（3，0）两点，‎ ‎∴‎9a-6+c=0‎c=-3‎，‎ ‎∴a=1‎c=-3‎，‎ ‎∴抛物线的解析式为y＝x2﹣2x﹣3，‎ ‎∵直线y＝kx+b经过A（0，﹣3）、B（3，0）两点，‎ ‎∴‎3k+b=0‎b=-3‎，解得：k=1‎b=-3‎，‎ ‎∴直线AB的解析式为y＝x﹣3，‎ ‎（2）∵y＝x2﹣2x﹣3＝（x﹣1）2﹣4，‎ ‎∴抛物线的顶点C的坐标为（1，﹣4），‎ ‎∵CE∥y轴，‎ ‎∴E（1，﹣2），‎ ‎∴CE＝2，‎ ‎①如图，若点M在x轴下方，四边形CEMN为平行四边形，则CE＝MN，‎ 设M（a，a﹣3），则N（a，a2﹣2a﹣3），‎ ‎∴MN＝a﹣3﹣（a2﹣2a﹣3）＝﹣a2+3a，‎ ‎∴﹣a2+3a＝2，‎ 解得：a＝2，a＝1（舍去），‎ ‎∴M（2，﹣1），‎ ‎②如图，若点M在x轴上方，四边形CENM为平行四边形，则CE＝MN，‎ 设M（a，a﹣3），则N（a，a2﹣2a﹣3），‎ ‎∴MN＝a2﹣2a﹣3﹣（a﹣3）＝a2﹣3a，‎ ‎∴a2﹣3a＝2，‎ 解得：a‎=‎‎3+‎‎17‎‎2‎，a‎=‎‎3-‎‎17‎‎2‎（舍去），‎ ‎∴M（‎3+‎‎17‎‎2‎，‎-3+‎‎17‎‎2‎），‎ 综合可得M点的坐标为（2，﹣1）或（‎3+‎‎17‎‎2‎‎，‎‎-3+‎‎17‎‎2‎）．‎ ‎（3）如图，作PG∥y轴交直线AB于点G，‎ 设P（m，m2﹣2m﹣3），则G（m，m﹣3），‎ ‎∴PG＝m﹣3﹣（m2﹣2m﹣3）＝﹣m2+3m，‎ ‎∴S△PAB＝S△PGA+S△PGB‎=‎1‎‎2‎PG⋅OB=‎1‎‎2‎×(-m‎2‎+3m)×3=-‎3‎‎2‎m‎2‎+‎9‎‎2‎m=-‎3‎‎2‎(m-‎3‎‎2‎‎)‎‎2‎+‎‎27‎‎8‎，‎ ‎∴当m‎=‎‎3‎‎2‎时，△PAB面积的最大值是‎27‎‎8‎，此时P点坐标为（‎3‎‎2‎‎，-‎‎3‎‎2‎）．‎ 声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布 日期：2019/6/30 10:01:25；用户：中考培优辅导；邮箱：p5193@xyh.com；学号：27411521‎