2010中考数学雄州考试试题 6页

绝密★‎ ‎2010年云南楚雄州高中（中专）招生统一考试 数学试题卷 ‎（全卷三个大题，共24小题，共8页；满分120分，考试时间120分钟）‎ 注意事项：‎ ‎1、本卷为试题卷，考生解题作答必须在答题卷上，答案书写在答题卷相应的位置上，在试题卷、草稿纸上作答无效 ‎2、考试结束后请将试题卷和答题卷一并交回。‎ 一、选择题（本大题共8小题，每小题只有一个正确选项，每小题3分，共24分）‎ ‎1、下列计算正确的是 A. B. C. D. ‎ ‎2、如图是由四个相同的小正方体组成的立体图形，它的左视图为 ‎3、自去年入秋以来，楚雄州遭遇了百年不遇的严重旱灾，截止‎2010年4月19日，楚雄州共收到各级各类抗旱救灾资金108014500元，这个数据用科学记数法表示为 A. B. C. D.‎ ‎4、一元二次方程的解是 A. B. C. D. ‎ ‎5、已知⊙和⊙的半径分别为‎2cm和‎3cm，两圆的圆心距为‎5cm，则两圆的位置关系是 A.外切 B. 外离 C. 相交 D. 内切 ‎6、已知等腰三角形的一个内角为70°，则另外两个内角的度数是 A.55°，55° B. 70°，40° C. 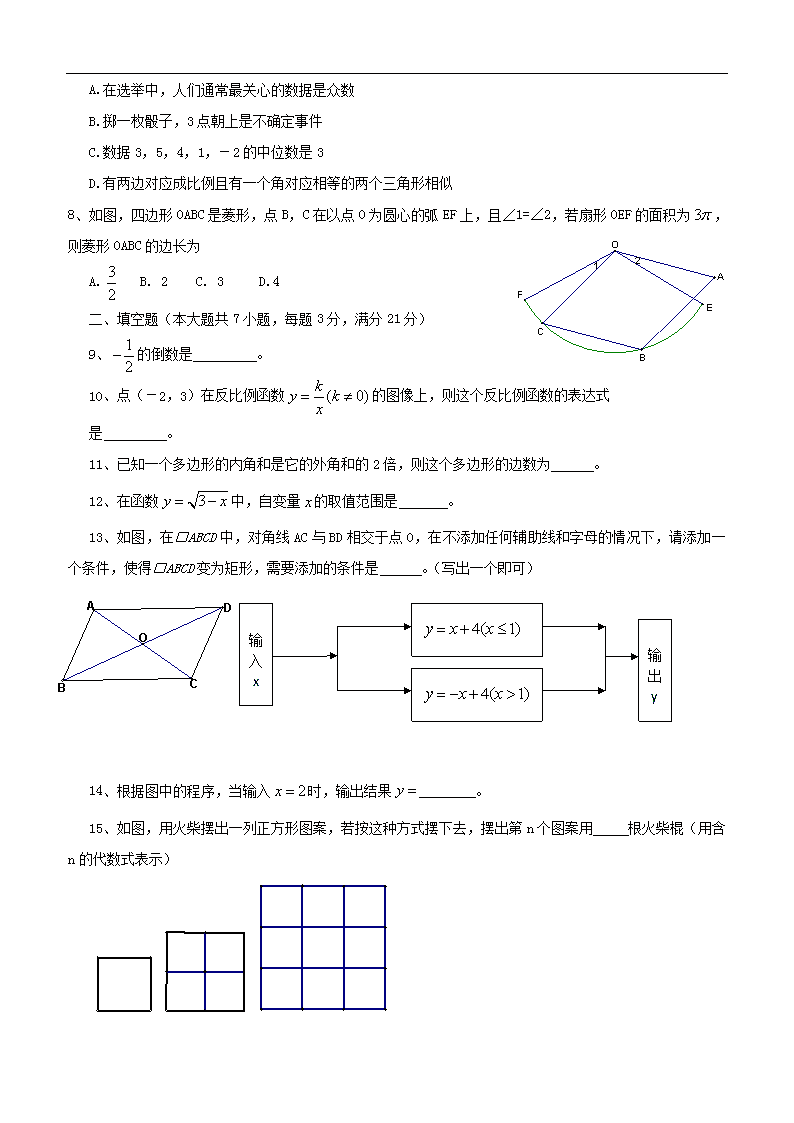55°，55°或70°，40° D.以上都不对 ‎7、下列说法不正确的是 A.在选举中，人们通常最关心的数据是众数 B.掷一枚骰子，3点朝上是不确定事件 C.数据3，5，4，1，－2的中位数是3‎ D.有两边对应成比例且有一个角对应相等的两个三角形相似 ‎8、如图，四边形OABC是菱形，点B，C在以点O为圆心的弧EF上，且∠1=∠2，若扇形OEF的面积为，则菱形OABC的边长为 A. B. ‎2 C. 3 D.4‎ 二、填空题（本大题共7小题，每题3分，满分21分）‎ ‎9、的倒数是 。‎ ‎10、点（－2，3）在反比例函数的图像上，则这个反比例函数的表达式 是 。‎ ‎11、已知一个多边形的内角和是它的外角和的2倍，则这个多边形的边数为 。‎ ‎12、在函数中，自变量的取值范围是 。‎ ‎13、如图，在□ABCD中，对角线AC与BD相交于点O，在不添加任何辅助线和字母的情况下，请添加一个条件，使得□ABCD变为矩形，需要添加的条件是 。（写出一个即可）‎ 输入x 输出y ‎14、根据图中的程序，当输入时，输出结果 。‎ ‎15、如图，用火柴摆出一列正方形图案，若按这种方式摆下去，摆出第n个图案用 根火柴棍（用含n的代数式表示）‎ 三、解答题（本大题共9个小题，满分75分）‎ ‎16、（本小题6分）先化简，再求值：，其中。‎ ‎17、（本小题7分）如图，点A、E、B、D在同一条直线上，AE=DB，AC=DF，AC∥DF.‎ 请探索BC与EF有怎样的位置关系？并说明理由。‎ ‎18、（本小题7分）△ABC在平面直角坐标系中的位置如图所示 ‎（1）作出△ABC关于轴对称的△,并写出点的坐标；‎ ‎（2）作出将△ABC 绕点O顺时针旋转180°后的△‎ ‎19、（本小题8分）小明和小华为了获得一张2010年上海世博园门票，他们各自设计了一个方案：‎ ‎ 小明的方案是：转动如图所示的转盘，当转盘停止转动后，如果指针停在阴影区域，则小明获得门票；如果指针停在白色区域，则小华获得门票（转盘被等分成6个扇区，若指针停在边界处，则重新转动转盘）。‎ 小华的方案是 ‎：有三张卡片，上面分别标有数字1，2，3，将它门背面朝上洗匀后，从中摸出一张，记录下卡片上的数字后放回，重新洗匀后再摸出一张，若摸出两张卡片上的数字之和为偶数，则小华获得门票。‎ ‎（1）在小明的方案中，计算小明获得门票的概率，并说明小明的方案是否公平？‎ ‎（2）用树状图或列表法例举小华设计方案中可能出现的所有结果，计算小华获得门票的概率，并说明小华的方案是否公平？‎ ‎20、（本小题8分）如图，河流的两岸PQ，MN互相平行，河岸PQ上有一排小树，已知相邻两树之间的距离CD=‎50米，某人在河岸MN的A处测的∠DAN=35°，然后沿河岸走了‎120米到达B处，测的∠CBN=70°，求河流的宽度CE（结果保留两个有效数字）。‎ ‎（参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70‎ Sin70°≈0.94，cos70°≈0.34，tan70°≈2.75）‎ ‎21、（本小题9分）在2009年楚雄州“火把节”房交会期间，某房地产公司对参加本次房交会的消费者进行了随机的问卷调查，共发放1000份调查问卷，并全部收回。‎ 根据问卷调查，将消费者年收入的情况整理后，制成表格如下：‎ 年收入 ‎1.2‎ ‎1.8‎ ‎3.0‎ ‎5.0‎ ‎10.0‎ 被调查的消费者数（人）‎ ‎200‎ ‎500‎ a ‎70‎ ‎30‎ 根据调查问卷，将消费者打算购买住房面积的情况整理后，作出部分频数分布直方图和扇形统计图。‎ ‎ ‎ 注：每组包含最小值不包含最大值，且住房面积取整数 根据以上信息回答下列问题：‎ ‎（1）根据表格可得a= ，被调查的1000名消费者的平均年收入为 万元，‎ ‎（2）补全频数分布直方图和扇形统计图。‎ ‎（3）若楚雄州现有购房打算的约有40000人，请估计购房面积在80至120平方米的大约有多少人？‎ ‎22、（本小题8分）已知：如图，抛物线与轴相交于两点A(1,0),B(3,0).与轴相较于点C（0，3）.‎ ‎（1）求抛物线的函数关系式；‎ ‎（2）若点D（）是抛物线上一点，请求出的值，并求处此时△ABD 的面积。‎ ‎23、（本小题9分）今年四月份，李大叔收获洋葱30吨，黄瓜13吨。现计划租用甲、乙两种货车共10辆将这两种蔬菜全部运往外地销售，已知一辆甲种货车可装洋葱4吨和黄瓜1吨，一辆乙种货车可装洋葱和黄瓜各2吨。‎ ‎（1）李大叔安排甲、乙两种货车时有几种方案.请你帮助设计出来；‎ ‎（2）若甲种货车每辆要付运费2000元，乙种货车每辆付运费1300元，请你帮助李大叔算一算应选哪种方案，才能使运费最少？最少运费是多少？‎ ‎24、（本小题13分）已知：如图，⊙A与轴交于C、D两点，圆心A的坐标为（1，0），‎ ‎⊙A的半径为，过点C作⊙A的切线交于点B（－4，0）。‎ ‎（1）求切线BC的解析式；‎ ‎（2）若点P是第一象限内⊙A上一点，过点P作⊙A的切线与直线BC相交于点G，且∠CGP=120°，求点G的坐标；‎ ‎（3）向左移动⊙A（圆心A始终保持在上），与直线BC交于E、F，在移动过程中是否存在点A，使得△AEF是直角三角形？若存在，求出点A 的坐标，若不存在，请说明理由。‎