2020-2021学年辽宁省丹东市东港市八年级上学期期中数学试卷 （解析版） 20页

2020-2021 学年辽宁省丹东市东港市八年级第一学期期中数学试 卷 一、选择题 1．（2 分）满足 的整数 x 有（ ） A．1 个 B．2 个 C．3 个 D．4 个 2．（2 分）若点 A（a，5），在第二象限，则点 A 关于直线 m（直线 m 上各点的横坐标都 是 1）对称的点坐标是（ ） A．（﹣a，5） B．（2﹣a，5） C．（﹣a﹣4，﹣5） D．（﹣a﹣2，﹣5） 3．（2 分）点 A（﹣5，y1）和 B（﹣2，y2）都在直线 y＝﹣3x 上，则 y1 与 y2 的关系是（ ） A．y1≤y2 B．y1＝y2 C．y1＜y2 D．y1＞y2 4．（2 分）一次函数 y＝kx+b 的图象如图所示，则关于 x 的方程 kx+b＝2 的解为（ ） A．x＝1 B．x＝2 C．x＝3 D．无法判断 5．（2 分）如图，是由四个全等的直角三角形与中间一个小正方形拼成的个大正方形，若 大正方形的面积是 17，小正方形的面积是 1，直角三角形的两直角边分别为 a，b，则（a+b） 2 的值是（ ） 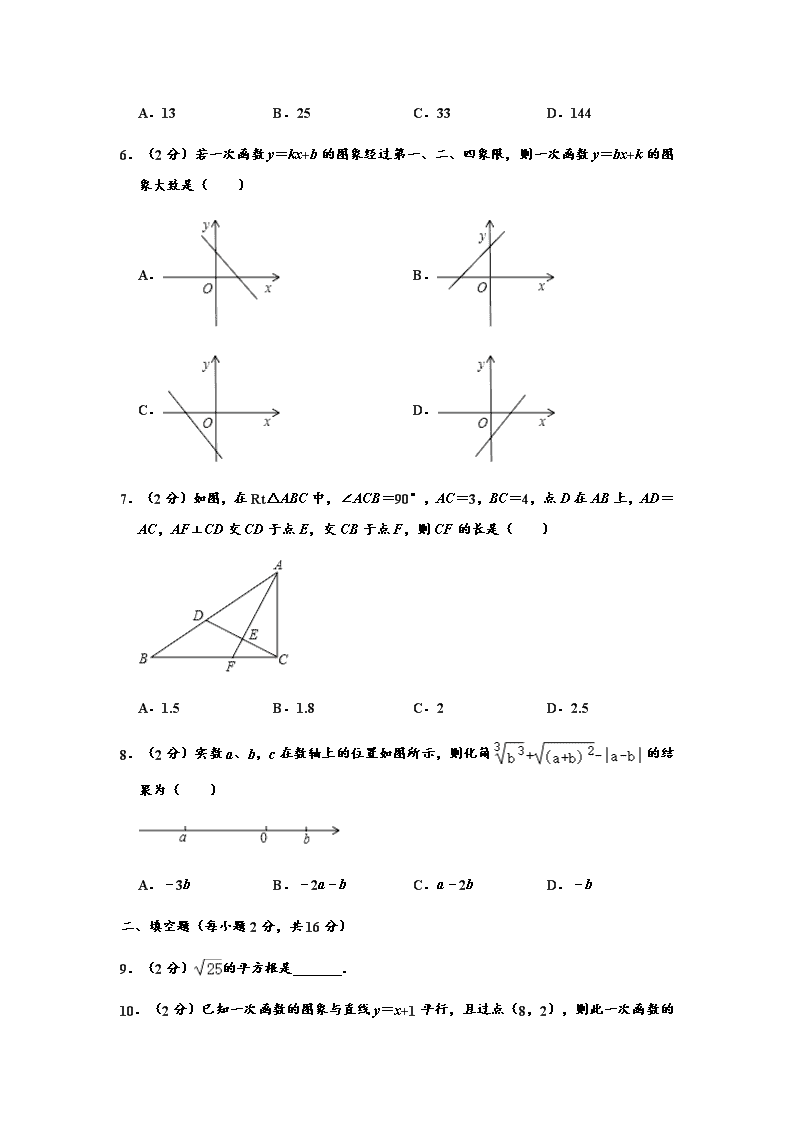A．13 B．25 C．33 D．144 6．（2 分）若一次函数 y＝kx+b 的图象经过第一、二、四象限，则一次函数 y＝bx+k 的图 象大致是（ ） A． B． C． D． 7．（2 分）如图，在 Rt△ABC 中，∠ACB＝90°，AC＝3，BC＝4，点 D 在 AB 上，AD ＝AC，AF⊥CD 交 CD 于点 E，交 CB 于点 F，则 CF 的长是（ ） A．1.5 B．1.8 C．2 D．2.5 8．（2 分）实数 a、b，c 在数轴上的位置如图所示，则化简 的结 果为（ ） A．﹣3b B．﹣2a﹣b C．a﹣2b D．﹣b 二、填空题（每小题 2 分，共 16 分） 9．（2 分） 的平方根是 ． 10．（2 分）已知一次函数的图象与直线 y＝x+1 平行，且过点（8，2），则此一次函数的 表达式为 ． 11．（2 分）平方根等于本身的数是 ． 12．（2 分）△ABC 中，AB＝15，AC＝13，高 AD＝12，则△ABC 的周长是 ． 13．（2 分）在 Rt△ABC 中，两边长分别为 a，b，且满足 ，则该直角 三角形的第三边长为 ． 14．（2 分）式子 成立的条件是 ． 15．（2 分）一个圆桶儿，底面直径为 16cm，高为 18cm，有一只小虫从底部点 A 处爬到上 底 B 处，则小虫所爬的最短路径长是（ π 取 3） ． 16．（2 分）如图，直线 CD 与 x 轴、y 轴正半轴分别交于 C、D 两点，∠OCD＝45°，第 四象限的点 P（m，n）在直线 CD 上，且 mn＝﹣6，则 OP2﹣OC2 的值为 ． 三、计算题（本题共 2 道小题，第 17 题每题 4 分第 18 题每题 4 分，共 16 分） 17．（8 分）（1） ． （2） ． 18．（8 分）（1） ． （2） ． 四.（本题 6 分） 19．（6 分）如图，在正方形网格中，每个小正方形的边长都为 1，点 A、点 B 在网格中的 位置如图所示， （1）建立适当的平面直角坐标系，使点 A、点 B 的坐标分别为（﹣2，3）、（﹣1，﹣4）． （2）点 C 的坐标为（﹣5，﹣1），在平面直角坐标系中标出点 C 的位置，连接 AB、BC、 CA． （3）作出△ABC 关于 y 轴对称的图形△A1B1C1． （4）直接写出△ABC 是何特殊的三角形． 五、解答题：（本题共 2 道小题，每题 8 分，共 16 分） 20．（8 分）已知 5a+2 的立方根是 3，3a+b﹣1 的算术平方根是 4． （1）求 a，b 的值． （2）求 4a﹣b 的平方根． 21．（8 分）如图，在四边形 ABCD 中，∠B＝90°，AB＝BC＝4，CD＝6，DA＝2．求∠ DAB 的度数． 六、（本题共 2 道小题，每题 9 分，共 18 分） 22．（9 分）如图，直线 与 x 轴、y 轴分别交于 A、B 两点，在 y 轴上有一点 N （0，4），动点 M 从点 A 以每秒 1 个单位的速度匀速沿 x 轴向左运动，点 M 的运动时 间为 t 秒． （1）求点 A、点 B 的坐标， （2）当△NOM 的面积为 6 时，求 t 值． （3）在 y 轴右侧，当△NOM≌△AOB 时，若点 G 是线段 ON 上一点，连结 MG，△MGN 沿 MG 折叠，点 N 恰好落在 x 轴上，直接写出此时点 G 的坐标． 23．（9 分）小明和爸爸进行登山锻炼，两人从山脚下出发，沿相同路线匀速上山，小明用 8 分钟登上山顶，此时爸爸距离出发地 280 米，小明登上山顶立即按原路匀速下山，与 爸爸相遇后，和爸爸一起以原下山速度返回出发地．小明、爸爸在锻炼过程中离出发地 的路程 y1（米）、y2（米）与小明出发的时间 x（分）的函数关系如图，根据图象信息解 答下列问题， （1）图中 a＝ ；b＝ ；c＝ ． （2）小明上山速度为 米/分；爸爸上山速度为 米/分， （3）直接写出小明与爸爸何时相距 30 米． 七、（本题 12 分） 24．（12 分）如图，直线 l1 的表达式为 y＝ax+2，且 l1 与 y 轴交于点 D，直线 l2 经过点 A （4，0），B（0，﹣1），两直线交于点 C（m， ）， （1）求直线 l1、l2 的表达式． （2）点 D 坐标为 ． （3）求△BCD 的面积． （4）若有过点 C 的直线 CE 把△BCD 的面积分为 2：1 两部分，请直接写出符合条件的 直线 CE 的表达式． 参考答案 一、选择题（下列各题的备选答案中，只有一个答案是正确的，每小题 2 分，共 16 分） 1．（2 分）满足 的整数 x 有（ ） A．1 个 B．2 个 C．3 个 D．4 个 解：∵1＜ ＜2， ∴﹣2＜﹣ ＜﹣1， 又∵1＜ ＜2，﹣ ＜x＜ ， ∴整数 x 为﹣1，0，1， 故选：C． 2．（2 分）若点 A（a，5），在第二象限，则点 A 关于直线 m（直线 m 上各点的横坐标都 是 1）对称的点坐标是（ ） A．（﹣a，5） B．（2﹣a，5） C．（﹣a﹣4，﹣5） D．（﹣a﹣2，﹣5） 解：∵直线 m 上各点的横坐标都是 1， ∴直线为：x＝1， ∵点 P（a，5）在第二象限， ∴a 到 1 的距离为：1﹣a， ∴点 P 关于直线 m 对称的点的横坐标是：1﹣a+1＝2﹣a， 故 P 点对称的点的坐标是：（2﹣a，5）． 故选：B． 3．（2 分）点 A（﹣5，y1）和 B（﹣2，y2）都在直线 y＝﹣3x 上，则 y1 与 y2 的关系是（ ） A．y1≤y2 B．y1＝y2 C．y1＜y2 D．y1＞y2 解：∵一次函数中一次项系数﹣3＜0，﹣5＜﹣2， ∴y1＞y2． 故选：D． 4．（2 分）一次函数 y＝kx+b 的图象如图所示，则关于 x 的方程 kx+b＝2 的解为（ ） A．x＝1 B．x＝2 C．x＝3 D．无法判断 解：观察图象知道一次函数 y＝kx+b（k、b 为常数，且 k≠0）的图象经过点（1，2）， 所以关于 x 的方程 kx+b＝2 的解为 x＝1， 故选：A． 5．（2 分）如图，是由四个全等的直角三角形与中间一个小正方形拼成的个大正方形，若 大正方形的面积是 17，小正方形的面积是 1，直角三角形的两直角边分别为 a，b，则（a+b） 2 的值是（ ） A．13 B．25 C．33 D．144 解：根据题意，结合勾股定理 a2+b2＝17， 四个三角形的面积＝4× ab＝17﹣1， ∴2ab＝16， 联立解得：（a+b）2＝17+16＝33． 故选：C． 6．（2 分）若一次函数 y＝kx+b 的图象经过第一、二、四象限，则一次函数 y＝bx+k 的图 象大致是（ ） A． B． C． D． 解：一次函数 y＝kx+b 过一、二、四象限， 则函数值 y 随 x 的增大而减小，因而 k＜0； 图象与 y 轴的正半轴相交则 b＞0， 因而一次函数 y＝bx﹣k 的一次项系数 b＞0， y 随 x 的增大而增大，经过一三象限， 常数项 k＜0，则函数与 y 轴负半轴相交， 因而一定经过一三四象限， 故选：D． 7．（2 分）如图，在 Rt△ABC 中，∠ACB＝90°，AC＝3，BC＝4，点 D 在 AB 上，AD ＝AC，AF⊥CD 交 CD 于点 E，交 CB 于点 F，则 CF 的长是（ ） A．1.5 B．1.8 C．2 D．2.5 解：连接 DF，如图所示： ∵在 Rt△ABC 中，∠ACB＝90°，AC＝3，BC＝4， ∴AB＝ ＝5， ∵AD＝AC＝3，AF⊥CD， ∴CE＝DE，BD＝AB﹣AD＝2， ∴CF＝DF， 在△ADF 和△ACF 中， ， ∴△ADF≌△ACF（SSS）， ∴∠ADF＝∠ACF＝90°， ∴∠BDF＝90°， 设 CF＝DF＝x，则 BF＝4﹣x， 在 Rt△BDF 中，由勾股定理得：DF2+BD2＝BF2， 即 x2+22＝（4﹣x）2， 解得：x＝1.5； ∴CF＝1.5； 故选：A． 8．（2 分）实数 a、b，c 在数轴上的位置如图所示，则化简 的结 果为（ ） A．﹣3b B．﹣2a﹣b C．a﹣2b D．﹣b 解：原式＝b+|a+b|﹣|a﹣b| ＝b+（﹣a﹣b）﹣（b﹣a） ＝b﹣a﹣b﹣b+a ＝﹣b， 故选：D． 二、填空题（每小题 2 分，共 16 分） 9．（2 分） 的平方根是 ． 解： ＝5，5 的平方根是 ， 故答案为： ． 10．（2 分）已知一次函数的图象与直线 y＝x+1 平行，且过点（8，2），则此一次函数的 表达式为 y＝x﹣6 ． 解：设所求一次函数的解析式为 y＝kx+b， ∵函数的图象与直线 y＝x+1 平行， ∴k＝1， ∵过点（8，2）， ∴2＝8+b， 解得 b＝﹣6， ∴一次函数的解析式为 y＝x﹣6， 故答案为：y＝x﹣6． 11．（2 分）平方根等于本身的数是 0 ． 解：∵02＝0， ∴平方根等于本身的是 0； 故答案是：0 12．（2 分）△ABC 中，AB＝15，AC＝13，高 AD＝12，则△ABC 的周长是 32 或 42 ． 解：此题应分两种情况说明： （1）当△ABC 为锐角三角形时，在 Rt△ABD 中， BD＝ ＝ ＝9， 在 Rt△ACD 中， CD＝ ＝ ＝5 ∴BC＝5+9＝14 ∴△ABC 的周长为：15+13+14＝42； （2）当△ABC 为钝角三角形时， 在 Rt△ABD 中，BD＝ ＝ ＝9， 在 Rt△ACD 中，CD＝ ＝ ＝5， ∴BC＝9﹣5＝4． ∴△ABC 的周长为：15+13+4＝32 ∴当△ABC 为锐角三角形时，△ABC 的周长为 42；当△ABC 为钝角三角形时，△ABC 的周长为 32． 综上所述，△ABC 的周长是 42 或 32． 故填：42 或 32． 13．（2 分）在 Rt△ABC 中，两边长分别为 a，b，且满足 ，则该直角 三角形的第三边长为 5 或 ． 解：∵a2﹣6a+9+ ＝0， ∴（a﹣3）2+ ＝0， ∴a﹣3＝0，b﹣4＝0， 解得，a＝3，b＝4， 当 4 是直角边时，第三边斜边＝ ＝5， 当 4 是斜边时，第三边＝ ＝ ， 故答案为：5 或 ． 14．（2 分）式子 成立的条件是 a≥4 ． 解：要使 有意义，必须 a﹣4≥0， 解得，a≥4， 故答案为：a≥4． 15．（2 分）一个圆桶儿，底面直径为 16cm，高为 18cm，有一只小虫从底部点 A 处爬到上 底 B 处，则小虫所爬的最短路径长是（ π 取 3） 30cm ． 解：展开圆柱的侧面如图，根据两点之间线段最短就可以得知 AB 最短．由题意，得 AC＝3×16÷2＝24，在 Rt△ABC 中，由勾股定理，得 AB＝ ＝ ＝30cm． 故答案为：30cm． 16．（2 分）如图，直线 CD 与 x 轴、y 轴正半轴分别交于 C、D 两点，∠OCD＝45°，第 四象限的点 P（m，n）在直线 CD 上，且 mn＝﹣6，则 OP2﹣OC2 的值为 12 ． 解：如图，过 P 作 PE⊥y 轴于 E，则 OC∥PE， ∴∠OCD＝∠DPE＝45°， ∵∠DOC＝∠DEP＝90°， ∴OD＝OC，DE＝EP， ∵P（m，n）， ∴m＝OD﹣n， ∴OD＝m+n， 两边同时平方得：OD2＝m2+n2+2mn， ∵mn＝﹣6， ∴m2+n2＝OD2+12， 由勾股定理得：OP2﹣OC2＝m2+（﹣n）2﹣OD2＝OD2+12﹣OD2＝12， 故答案为 12． 三、计算题（本题共 2 道小题，第 17 题每题 4 分第 18 题每题 4 分，共 16 分） 17．（8 分）（1） ． （2） ． 解：（1）原式＝3 ﹣2 ﹣ ＝ ； （2）原式＝ ﹣ ＝ ﹣2 ＝﹣ ． 18．（8 分）（1） ． （2） ． 解：（1）原式＝[（ ﹣ ）（ + ）]2019×（ + ） ＝﹣1×（ + ） ＝﹣ ﹣ ； （2）原式＝4 +3﹣ + ﹣1 ＝5 + ． 四.（本题 6 分） 19．（6 分）如图，在正方形网格中，每个小正方形的边长都为 1，点 A、点 B 在网格中的 位置如图所示， （1）建立适当的平面直角坐标系，使点 A、点 B 的坐标分别为（﹣2，3）、（﹣1，﹣4）． （2）点 C 的坐标为（﹣5，﹣1），在平面直角坐标系中标出点 C 的位置，连接 AB、BC、 CA． （3）作出△ABC 关于 y 轴对称的图形△A1B1C1． （4）直接写出△ABC 是何特殊的三角形． 解：（1）如图所示； （2）如图所示； （3）如图所示：△A1B1C1 即为所求； （4）△ABC 是等腰直角三角形． 五、解答题：（本题共 2 道小题，每题 8 分，共 16 分） 20．（8 分）已知 5a+2 的立方根是 3，3a+b﹣1 的算术平方根是 4． （1）求 a，b 的值． （2）求 4a﹣b 的平方根． 解：（1）∵5a+2 的立方根是 3，3a+b﹣1 的算术平方根是 4， ∴5a+2＝27，3a+b﹣1＝16， ∴a＝5，b＝2； （2）由（1）知 a＝5，b＝2， ∴4a﹣b＝4×5﹣2＝18， ∴4a﹣b 的平方根为±3 ． 21．（8 分）如图，在四边形 ABCD 中，∠B＝90°，AB＝BC＝4，CD＝6，DA＝2．求∠ DAB 的度数． 解：∵∠B＝90°，AB＝BC＝4， ∴AC＝ ，∠DAB＝∠DBA＝45°， ∵（4 ）2+22＝62， ∴AC2+DA2＝CD2， ∴△ACD 是直角三角形， ∵∠DAC 是 CD 所对的角， ∴∠DAC＝90°， ∴∠DAB＝∠DAC+∠BAC＝90°+45°＝135°． 六、（本题共 2 道小题，每题 9 分，共 18 分） 22．（9 分）如图，直线 与 x 轴、y 轴分别交于 A、B 两点，在 y 轴上有一点 N （0，4），动点 M 从点 A 以每秒 1 个单位的速度匀速沿 x 轴向左运动，点 M 的运动时 间为 t 秒． （1）求点 A、点 B 的坐标， （2）当△NOM 的面积为 6 时，求 t 值． （3）在 y 轴右侧，当△NOM≌△AOB 时，若点 G 是线段 ON 上一点，连结 MG，△MGN 沿 MG 折叠，点 N 恰好落在 x 轴上，直接写出此时点 G 的坐标． 解：（1）在 y＝﹣ x+2 中，令 y＝0 可求得 x＝4，令 x＝0 可得 y＝2， ∴A（4，0），B（0，2）． （2）∵A（4，0），B（0，2），N（0，4）， ∴OB＝2，ON＝OA＝4， 由题意可知 OM＝|4﹣t|， ∵△NOM 的面积为 6， ∴ •|4﹣t|×4＝6， ∴t＝1 或 7， 即当 t 的值为 1 或 7 时，△NOM 的面积为 6． （3）如图，由△NOM≌△AOB，得 OM＝OB＝2，且 ON＝4， ∴MN＝ ＝2 ， ∵△MGN 沿 MG 折叠得到△MGH， ∴MH＝MN，NG＝HG， ∴HO＝MH﹣OM＝2 ﹣2， 设 G 点坐标为（0，y）， ∵点 G 是线段 ON 上一点， ∴OG＝y，则 HG＝NG＝4﹣y， 在 Rt△BOH 中，由勾股定理可得（2 ﹣2）2+y2＝（4﹣y）2，解得 y＝ ﹣1， ∴G 点坐标为（0， ﹣1）． 23．（9 分）小明和爸爸进行登山锻炼，两人从山脚下出发，沿相同路线匀速上山，小明用 8 分钟登上山顶，此时爸爸距离出发地 280 米，小明登上山顶立即按原路匀速下山，与 爸爸相遇后，和爸爸一起以原下山速度返回出发地．小明、爸爸在锻炼过程中离出发地 的路程 y1（米）、y2（米）与小明出发的时间 x（分）的函数关系如图，根据图象信息解 答下列问题， （1）图中 a＝ 8 ；b＝ 280 ；c＝ 10 ． （2）小明上山速度为 50 米/分；爸爸上山速度为 35 米/分， （3）直接写出小明与爸爸何时相距 30 米． 【解答】（1）根据题意，可知 a＝8，b＝280， 小明下山用的时间为：24﹣8＝16（分钟），下山的速度为：400÷16＝25（米/分钟）， 设小明与爸爸相遇的时间为 x 分， （280÷8）x＝400﹣25（x﹣8）， 解得，x＝10， 故 c＝10， 故答案为：8；280；10； （2）小明上山速度为 400÷8＝50（米/分）；爸爸上山速 280÷8＝35（米/分）； 故答案为：50；35； （3）根据题意得：（50﹣35）x＝30 或 25（x﹣8）+35x＝400﹣30， 解得 x＝2 或 ， 答：2 分或 分时两人相距 30 米． 七、（本题 12 分） 24．（12 分）如图，直线 l1 的表达式为 y＝ax+2，且 l1 与 y 轴交于点 D，直线 l2 经过点 A （4，0），B（0，﹣1），两直线交于点 C（m， ）， （1）求直线 l1、l2 的表达式． （2）点 D 坐标为 （0，2） ． （3）求△BCD 的面积． （4）若有过点 C 的直线 CE 把△BCD 的面积分为 2：1 两部分，请直接写出符合条件的 直线 CE 的表达式． 解：（1）设直线 l2 的解析式为 y＝kx+b， ∵直线 l2 经过点 A（4，0），B（0，﹣1）， ∴ ，解得 ， ∴直线 l2 的解析式为 y＝ x﹣1， ∵两直线交于点 C（m， ）， ∴﹣ ＝ m﹣1，解得 m＝ ， ∴C（ ，﹣ ）， 把 C 的坐标代入 y＝ax+2 得，﹣ ＝ a+2， 解得 a＝﹣2， ∴直线 l1 的表达式为 y＝﹣2x+2； （2）把 x＝0 代入 y＝﹣2x+2，可得：y＝2， 所以点 D 的坐标为（0，2）， 故答案为：（0，2）； （3）∵B（0，﹣1），D（0，2），C（ ，﹣ ）， ∴BD＝3， ∴S△BCD＝ ＝2； （4）当过点 C 的直线 CE 把△BCD 的面积分为 2：1 两部分时，则 DE：EB＝2：1 或 DE：EB＝1：2， ∵B（0，﹣1），D（0，2）， ∴当 DE：EB＝2：1 时，则点 E 的坐标为（0，0） 当 DE：EB＝1：2 时，则 E 的坐标为（0，1）， 设直线 CE 的解析式为 y＝cx 或 y＝cx+1， 把（ ，﹣ ）代入 y＝cx 得﹣ ＝ c，解得 c＝﹣ 把（ ，﹣ ）代入 y＝cx+1 得﹣ ＝ c+1，解得 c＝﹣ ∴直线 CE 的表达式为：y＝﹣ x 或 y＝﹣ x+1．