中考数学二轮精品练习：解三角形 3页

‎ ‎ 解三角形 ‎ 班级 姓名 学号 ‎ 复习目标：‎ ‎1．能利用三角函数的定义，在一个直角三角形中，利用已知的边和角，求未知的边和角.‎ ‎2．知道坡度、仰角、俯角的含义.‎ ‎3．能将实际问题转化为数学问题 ，建立数学模型，解决问题.‎ 过程设计：‎ 一、知识回顾 ‎1.填空：‎ ‎（1）若地面上的甲看到高山上的乙的仰角为20o，则乙看到甲的俯角为 .‎ ‎（2）已知一斜坡的坡度为1﹕4，水平距离为20m，则该斜坡的垂直高度为 .‎ ‎2.选择：‎ ‎（1）河堤的横断面如图1所示，堤高BC是5m，迎水斜坡AB长13m，那么斜坡AB的坡度等于（ ）‎ A、1﹕3 B、1﹕2.6 C、1﹕2.4 D、1﹕2‎ ‎（2）为了测量学校某教学楼的高度，在距离该教学楼30m的A处，测得楼顶的仰角为a，则教学楼的高为 （ ）‎ ‎30‎ sinα tanα ‎30‎ A．──── B．30 tanα C．30sinα D．────‎ ‎（3）如图2，在梯形ABCD中，AD∥BC，∠B=45 o，∠C=120 o，AB=8，则CD的长为 ( ）‎ A． B．4 C． D．‎ ‎（4）菱形在平面直角坐标系中的位置如图3所示，，则点的坐标为 （ ）‎ A． B． C． D．‎x y O C B A ‎ ‎ 图1 图2 图3‎ 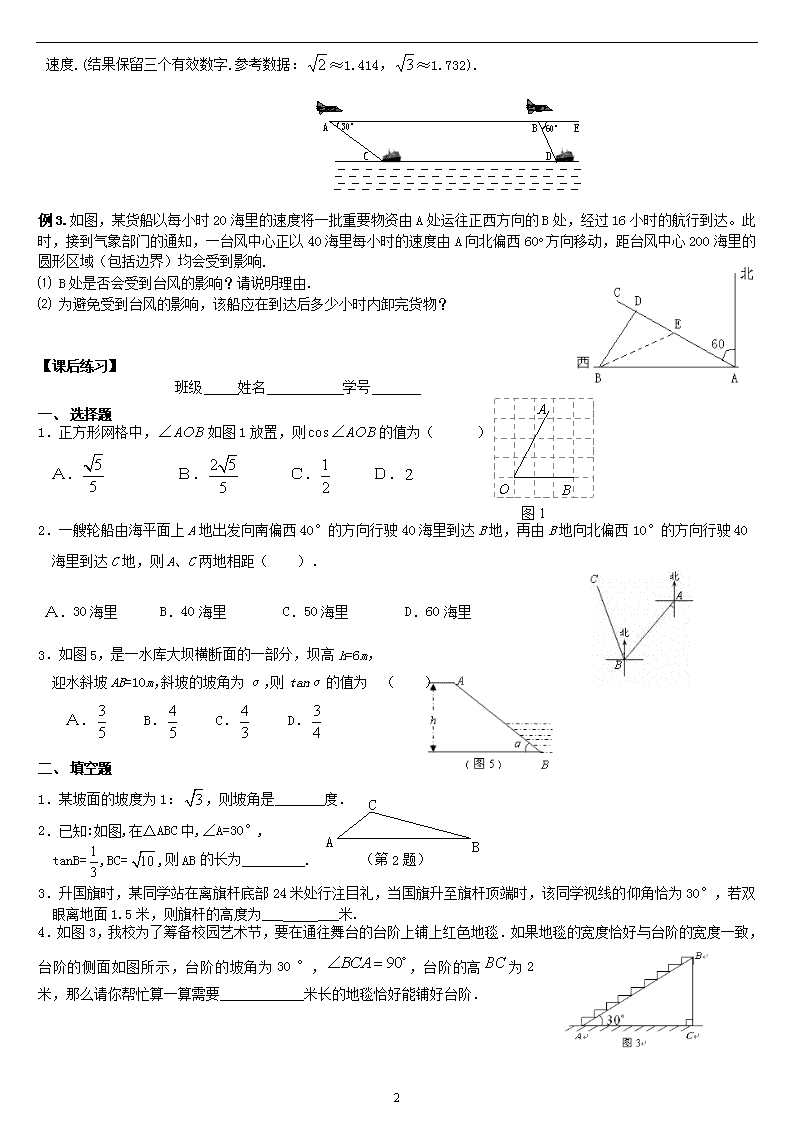二、例题解析 P A B E F ‎30º ‎45º ‎ 例1.如图所示，A、B两城市相距100km. 现计划在这两座城市间修筑一条高速公路（即线段AB），经测量，森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上. 已知森林保护区的范围在以P点为圆心，50km为半径的圆形区域内. 请问：计划修筑的这条高速公路会不会穿越保护区？ 为什么？（参考数据：，）‎ ‎ ‎ 例2 . 法航客机失事引起全球高度关注，为调查失事原因，巴西军方派出侦察机和搜救船在失事海域同时沿同一方向配合搜寻飞机残骸（如图）.在距海面900米的高空A处，侦察机测得搜救船在俯角为30°的海面C处，当侦察机以米/分的速度平行海面飞行20分钟到达B处后，测得搜救船在俯角为60°‎ 3‎ ‎ ‎ 的海面D处，求搜救船搜寻的平均速度.(结果保留三个有效数字.参考数据：≈1.414，≈1.732).‎ ‎ ‎ 例3.如图，某货船以每小时20海里的速度将一批重要物资由A处运往正西方向的B处，经过16小时的航行到达。此时，接到气象部门的通知，一台风中心正以40海里每小时的速度由A向北偏西60o方向移动，距台风中心200海里的圆形区域（包括边界）均会受到影响.‎ ‎⑴ B处是否会受到台风的影响？请说明理由.‎ ‎⑵ 为避免受到台风的影响，该船应在到达后多少小时内卸完货物？‎ ‎【课后练习】‎ 班级 姓名 学号 ‎ A B O 图1‎ 一、 选择题 ‎1．正方形网格中，如图1放置，则的值为（　 　）‎ Ａ． Ｂ． Ｃ． Ｄ．‎ ‎2．一艘轮船由海平面上A地出发向南偏西40°的方向行驶40海里到达B地，再由B地向北偏西10°的方向行驶40海里到达C地，则A、C两地相距（　　）．‎ Ａ．30海里   B．40海里    C．50海里    D．60海里 ‎3．如图5，是一水库大坝横断面的一部分，坝高h=6m，‎ 迎水斜坡AB=10m，斜坡的坡角为α，则tanα的值为 （ ）‎ Ａ． B． C． D．‎ 二、 填空题 ‎1．某坡面的坡度为1：，则坡角是_______度．‎ ‎2．已知:如图,在△ABC中,∠A=30°, ‎ ‎ tanB=,BC=,则AB的长为_________. 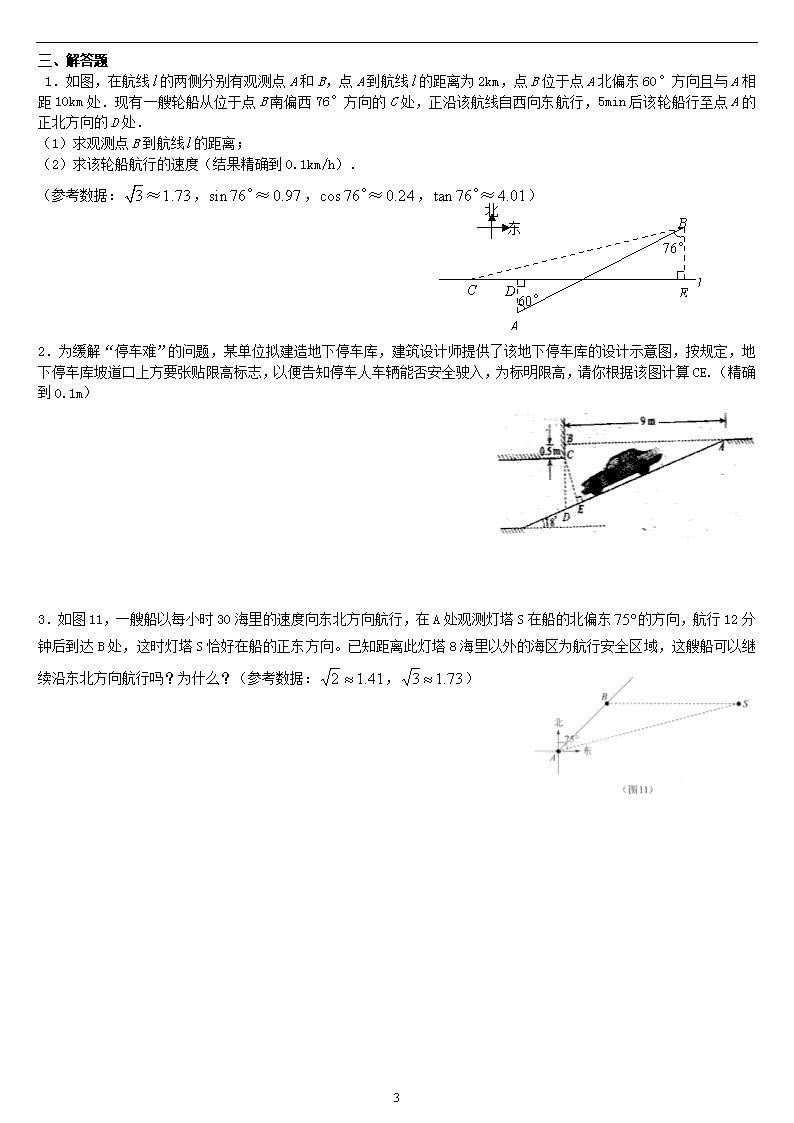（第2题）‎ ‎3．升国旗时，某同学站在离旗杆底部24米处行注目礼，当国旗升至旗杆顶端时，该同学视线的仰角恰为30°，若双眼离地面1.5米，则旗杆的高度为___ ___米.‎ ‎4．如图3，我校为了筹备校园艺术节，要在通往舞台的台阶上铺上红色地毯．如果地毯的宽度恰好与台阶的宽度一致，台阶的侧面如图所示，台阶的坡角为30°，，台阶的高为2米，那么请你帮忙算一算需要 米长的地毯恰好能铺好台阶．‎ 3‎ ‎ ‎ 三、解答题 ‎ ‎ 1．如图，在航线的两侧分别有观测点A和B，点A到航线的距离为2km，点B位于点A北偏东60°方向且与A相距10km处．现有一艘轮船从位于点B南偏西76°方向的C处，正沿该航线自西向东航行，5min后该轮船行至点A的正北方向的D处．‎ ‎（1）求观测点B到航线的距离；‎ ‎（2）求该轮船航行的速度（结果精确到0.1km/h）．‎ 北 东 C D B E A l ‎60°‎ ‎76°‎ ‎（参考数据：，，，）‎ ‎2．为缓解“停车难”的问题，某单位拟建造地下停车库，建筑设计师提供了该地下停车库的设计示意图，按规定，地下停车库坡道口上方要张贴限高标志，以便告知停车人车辆能否安全驶入，为标明限高，请你根据该图计算CE.（精确到0.1m）‎ ‎3．如图11，一艘船以每小时30海里的速度向东北方向航行，在A处观测灯塔S在船的北偏东的方向，航行12分钟后到达B处，这时灯塔S恰好在船的正东方向。已知距离此灯塔8海里以外的海区为航行安全区域，这艘船可以继续沿东北方向航行吗？为什么？（参考数据：，）‎ 3‎