九年级上册青岛版数学课件4-7一元二次方程的应用（1） 24页

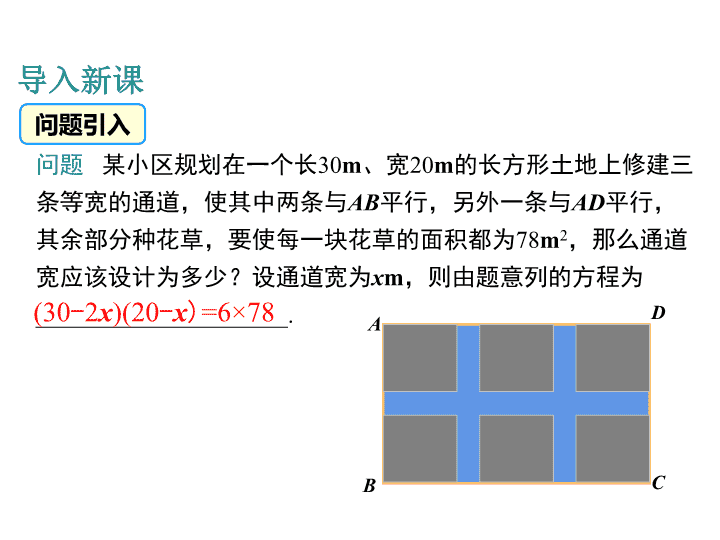
4.7一元二次方程的应用（1） 学习目标 1.掌握面积法建立一元二次方程的数学模型.（难点） 2.能运用一元二次方程解决与面积有关的实际问题. （重点） 导入新课 问题 某小区规划在一个长30m、宽20m的长方形土地上修建三 条等宽的通道，使其中两条与AB平行，另外一条与AD平行， 其余部分种花草，要使每一块花草的面积都为78m2，那么通道 宽应该设计为多少？设通道宽为xm，则由题意列的方程为 _____________________. CB DA(30-2x)(20-x)=6×78 问题引入 讲授新课 引例：要设计一本书的封面,封面长27㎝,宽21cm正中央是一 个与整个封面长宽比例相同的矩形,如果要使四周的边衬所占 面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等 宽,应如何设计四周边衬的宽度？ (精确到0.1cm) 27cm 21cm 合作探究 几何图形与一元二次方程 分析:这本书的长宽之比 ： 正中 央的矩形长宽之比 ： ，上下边衬 与左右边衬之比 ： . 9 7 9 7 27cm 21cm 解：设中央长方形的长和宽分别为9a 和7a由此得到上下边衬宽度之比为： 1 1(27 9 ) : (21 7 ) 2 2 a a  9 7 9(3 ) : 7(3 ) 9: 7. a a    27cm 21cm 解:设上下边衬的9xcm，左右边衬宽 为7xcm依题意得 3(27 18 )(21 14 ) 27 21, 4 x x     解方程得 6 3 3 . 4 x   故上下边衬的宽度为: 6 3 39 1.8, 4    故左右边衬的宽度为: 6 3 37 1.4. 4    方程的哪个根 合乎实际意义? 为什么? 试一试：如果换一种设未知数的方法，是否可以更简 单地解决上面的问题？ 解:设正中央的矩形两边别为9xcm， 7xcm.依题意得 27cm 21cm 39 7 27 21, 4 x x    解得 2 2 3 3 3 3 2 2 x x ， （舍去）. 故上下边衬的宽度为: 3 327 927 9 54 27 32 1.8. 2 2 4 x       3 321 721 7 42 21 32 1.4. 2 2 4 x       故左右边衬的宽度为: 建立一元二 次方程模型 实际问题 实际问题的解 解一元二次 方程 一元二次方程的根 检 验 运用一元二次方程模型解决实际问题的步骤有哪些？ 设未知数 分析数量关系 例1：如图所示，在△ABC中，∠C=90°， AC=6cm， BC=8cm.点P沿AC边从点A向终点C以1cm/s的速度移动；同时 点Q沿CB边从点C向终点B以2cm/s的速度移动，且当其中一点 到达终点时，另一点也随之停止移动.问点P，Q出发几秒后可 使△PCQ的面积为9 cm²？ 根据题意得AP= xcm,PC=(6-x)cm,CQ=2xcm 解：若设出发x s后可使△PCQ的面积为9cm² 整理，得 解得 x1= x2=3 答：点P，Q出发3s后可使△PCQ的面积为9cm². 92)6( 2 1  xx 0962  xx 主要集中在几何图形的面积问题, 这类问题的面 积公式是等量关系. 如果图形不规则应割或补成规则 图形,找出各部分面积之间的关系,再运用规则图形的 面积公式列出方程; 方法点拨 220 32 32 20 540x x x     20 32 x x 解：设道路的宽为x米 例2：如图，在一块宽为20m, 长为32m的矩形地面上 修筑同样宽的两条道路,余下的部分种上草坪,要使草 坪的面积为540㎡,求道路的宽为多少？ 典例精析 还有其他 解法吗？ 20 32 x x 解：设道路的宽为 x 米 20-x 32-x (32-x)(20-x)=540 整理，得x2-52x+100=0 解得 x1=2,x2=50 当x=50时，32-x=-18,不合题意，舍去. ∴取x=2 答：道路的宽为2米. 方法二： 在宽为20m, 长为32m的矩形地面 上修筑同样宽的道路,余下的部分种上草坪, 要使草坪的面积为540㎡,求这种方案下的 道路的宽为多少？ 解：设道路的宽为 x 米 (32-x)(20-x)=540 可列方程为 20 32 x xx 20-x 在宽为20m, 长为32m的矩形地面上修筑同样 宽的道路,余下的部分种上草坪,要使草坪的面积为 540m2,求这种种方案下的道路的宽为多少？ 解：设道路的宽为 x 米 (32-2x)(20-x)=540 可列方程为 32-2x 20 32 x xx x 20 32 2x 2x 32-2x 20-2x 在宽为20m, 长为32m的矩 形地面上修筑同样宽的道路,余下的 部分种上草坪,要使草坪的面积为 540m2,求这种种方案下的道路的宽 为多少？ 解：设道路的宽为 x 米 (32-2x)(20-2x)=540 可列方程为 在宽为20m, 长为32m的矩形地面上修筑四条道路,余下 的部分种上草坪，如果横、纵小路的宽度比为3：2， 且使小路所占面积是矩形面积的四分之一,求道路的宽 为多少？ 小路所占面积是矩形面积 的四分之一 剩余面积是矩形面积的 四分之三 解:设横、竖小路的宽度分别为3x、 2x， 于是可列方程 (30-4x)(20-6x)= —×20×30 20㎝ 30㎝ 3x 2x 30-4x 20-6x 4 3 3x 2x 6x 4x 30-4x 20-6x 我们利用“图形经过移动，它的面积大小不 会改变”的性质，把纵、横两条路移动一下，使 列方程容易些（目的是求出水渠的宽，至于实际 施工，仍可按原图的位置修路）. 方法点拨 解：设AB长是x m. (100-4x)x=400 x2-25x+100=0 x1=5，x2=20 x=20,100-4x=20<25 x=5,100-4x=80>25 x=5(舍去) 答：羊圈的边长AB和BC的长个是20m,20m. 例3：如图：要利用一面墙（墙长为25米）建羊圈，用 100米的围栏围成总面积为400平方米的三个大小相同的 矩形羊圈，求羊圈的边长AB和BC的长个是多少米？ D CB A 25米 变式：如图，一农户要建一个矩形猪舍，猪舍的一边利用长为 12m的住房墙，另外三边用25m长的建筑材料围成，为方便进 出，在垂直于住房墙的一边留一个1m的门，所围矩形猪舍的 长、宽分别为多少时，猪舍面积为80平方米？ 住房墙 1m 解：设矩形猪舍垂直于住房墙的一边长为x m， 由题意得 x(25-2x+1)=80 化简，得 x2-13x+40=0 解得 x1=5 , x2=8 当x=5时，26-2x=16>12 (舍去） 当x=8时，26-2x=10<12 故所围矩形猪舍的长为10m,宽为8m. 则平行于住房墙的一边长(25-2x+1)m. 1. 在一幅长80cm，宽50cm的矩形风景画的四周镶一条金色 纸边，制成一幅矩形挂图，如图所示，如果要使整个挂图 的面积是5400cm2，设金色纸边的宽为xcm，那么x满足的 方程是（ ） A．x2+130x-1400=0 B．x2+65x-350=0 C．x2-130x-1400=0 D．x2-65x-350=0 80cm xx xx 50cm B 当堂练习 2.一块长方形铁板，长是宽的2倍，如果在4个角上截去边 长为5cm的小正方形， 然后把四边折起来，做成一个没 有盖的盒子，盒子的容积是3000 cm3，求铁板的长和宽． 解：设铁板的宽为x cm,则有长为2x cm 5(2x-10)(x-10)=3000 x2-15x-250=0 解得 x1=25 x2=-10(舍去） 所以 2x=50 答：铁板的长50cm,宽为25cm. 3.如图，要设计一个宽20cm,长为30cm的矩形图案，其中有两横 两竖彩条，横竖彩条的宽度之比为2∶ 3 ，若使所有彩条的面积 是原来矩形图案面积的三分之一，应如何设计每个彩条的宽度？ 解：设横向彩条的宽度2xcm ,竖 彩条的宽度3xcm (20-6x)(30-4x)=400 6x2-65x+50=0 1 2 5 , 10( 6 x x  舍去） 5 52 ,3 3 2 x x 则 5 5cm, cm. 3 2 答：每个横竖条的宽度分别是 课堂小结 几何图 形与一 元二次 方程问 题 几何图形 常见几何图形面积 是等量关系. 类 型 课本封面问题 彩条/小路宽 度问题 常采用图形 平移能聚零 为整方便列 方程