人教版2021年中考数数学阶段复习巩固与提升微专题《锐角三角函数》专练 6页

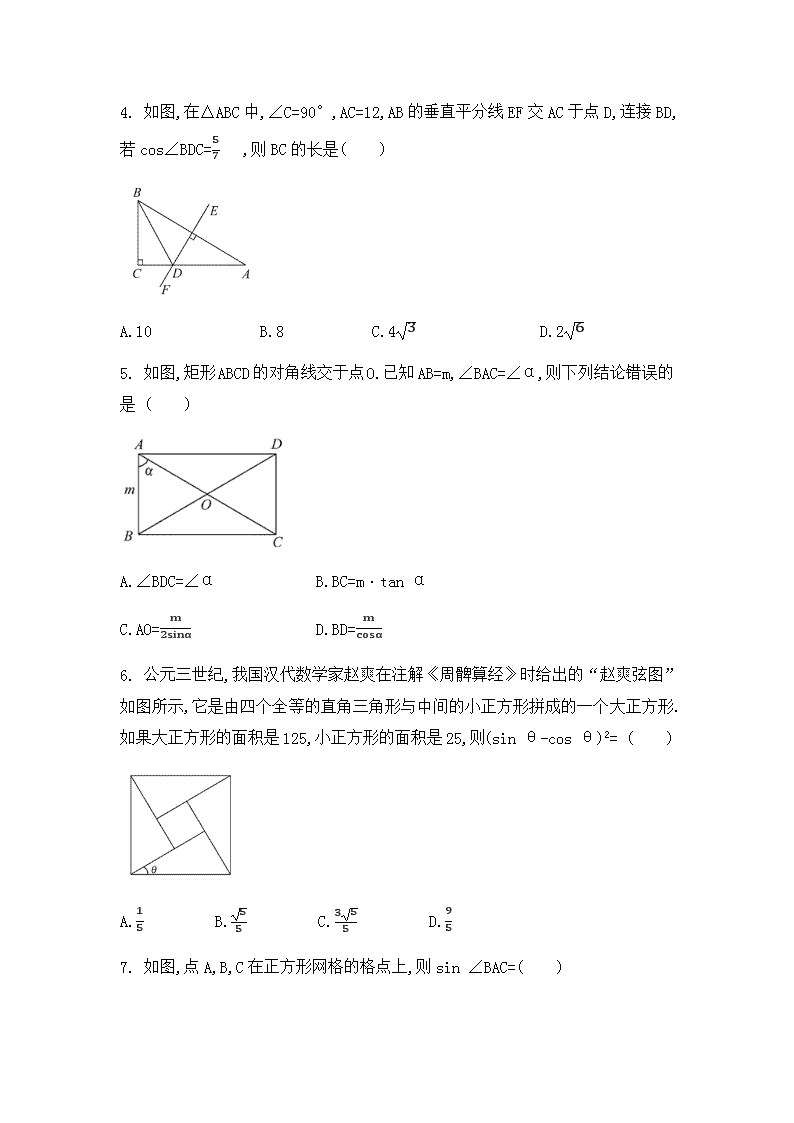
人教版 2021 年中考数数学阶段复习巩固与提升微专题 《锐角三角函数》专练 一．选择题. 1. 如图,△ABC 中,AC=5,cos B= 2 2 ,sin C= 3 5 ,则△ABC 的面积是( ) A. 21 2 B.12 C.14 D.21 2. 如图,在 Rt△ABC 中,∠ACB=90°,CD⊥AB 于 D,下列式子正确的是( ) A.sin A= BD BC B.cos A= AC ADC.tan A= CD AB D.cos B= AC AB3. 如图,在 6×6 的正方形网格中,△ABC 的顶点都在小正方形的顶点上,则 tan∠BAC 的值是( ) A. 4 5 B. 4 3 C. 3 4 D. 3 54. 如图,在△ABC 中,∠C=90°,AC=12,AB 的垂直平分线 EF 交 AC 于点 D,连接 BD, 若 cos∠BDC= 5 7 ,则 BC 的长是( ) A.10 B.8 C.4 3 D.2 65. 如图,矩形 ABCD的对角线交于点O.已知 AB=m,∠BAC=∠α,则下列结论错误的 是 ( ) A.∠BDC=∠α B.BC=m·tan α C.AO= m 2sinα D.BD= m cosα6. 公元三世纪,我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图” 如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形. 如果大正方形的面积是 125,小正方形的面积是 25,则(sin θ-cos θ)2= ( ) A. 1 5 B. 5 5 C. 3 5 5 D. 9 57. 如图,点 A,B,C 在正方形网格的格点上,则 sin ∠BAC=( ) A. 2 6 B. 26 26 C. 26 13 D. 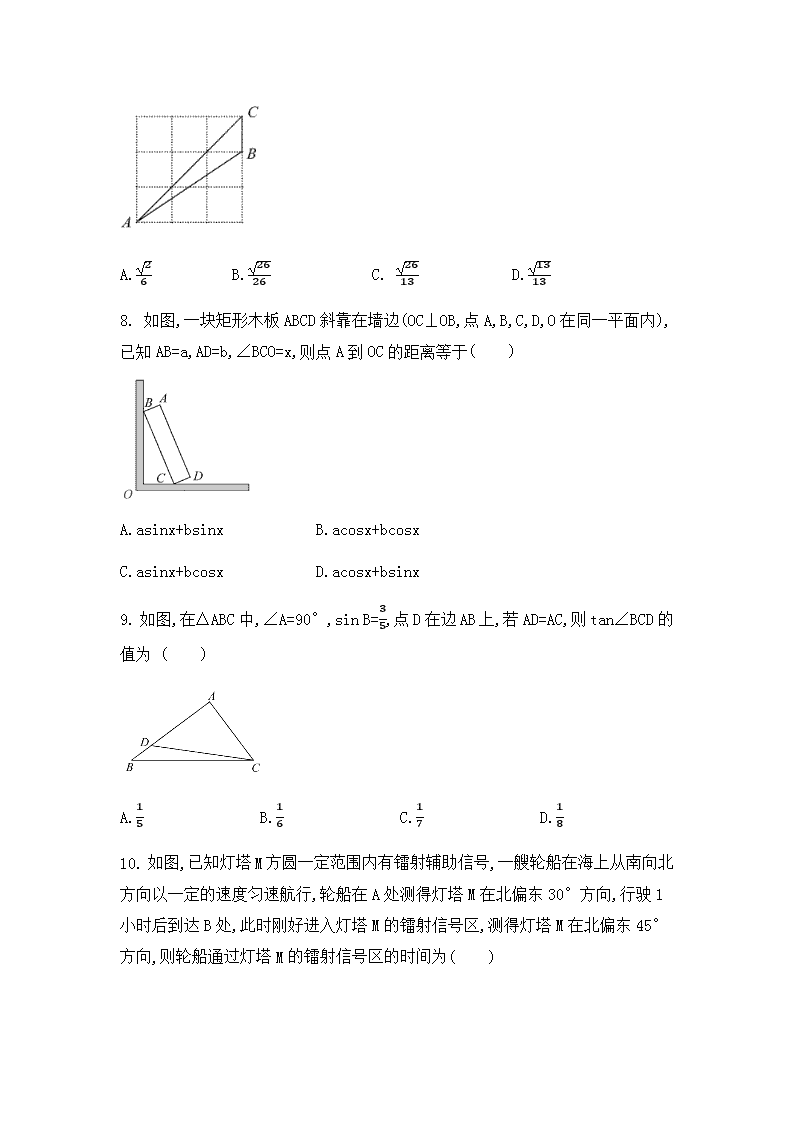13 138. 如图,一块矩形木板 ABCD 斜靠在墙边(OC⊥OB,点 A,B,C,D,O 在同一平面内), 已知 AB=a,AD=b,∠BCO=x,则点 A 到 OC 的距离等于( ) A.asinx+bsinx B.acosx+bcosx C.asinx+bcosx D.acosx+bsinx 9. 如图,在△ABC 中,∠A=90°,sin B= 3 5 ,点 D 在边 AB 上,若 AD=AC,则 tan∠BCD 的值为 ( ) A. 1 5 B. 1 6 C. 1 7 D. 1 810. 如图,已知灯塔 M 方圆一定范围内有镭射辅助信号,一艘轮船在海上从南向 北方向以一定的速度匀速航行,轮船在 A 处测得灯塔 M 在北偏东 30°方向,行驶 1 小时后到达 B 处,此时刚好进入灯塔 M 的镭射信号区,测得灯塔 M 在北偏东 45° 方向,则轮船通过灯塔 M 的镭射信号区的时间为( ) A.( 3 -1)小时 B.( 3 +1)小时 C.2 小时 D. 3 小时 二．填空题. 11. 在直角三角形 ABC 中,若 2AB=AC,则 cos C= . 12. 若∠a 为锐角,且 tan a 是方程 x2-2x-3=0 的一个根,则 sin a 等于 . 13. 三角板是我们学习数学的好帮手,将一对直角三角板如图放置,点 C 在 FD 的 延长线上,点 B 在 ED 上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则 CD 的长度是 . 14. 某型号飞机的机翼形状如图所示,根据图中数据计算 AB 的长为 m.(结果 保留根号) 15. 如图,在 Rt△AOB 中,∠AOB=90°,顶点 A,B 分别在反比例函数 y= 1 x (x>0) 与 y=- 5 x (x<0)的图象上,则 tan∠BAO 的值为 . 16. 在△ABC 中,若∠B=45°,AB=10 2 ,AC=5 5 ,则△ABC 的面积是 . 17. 如图,在 Rt△ABC 中,∠B=90°,AB=5,BC=12,将△ABC 绕点 A 逆时针旋转得到 △ADE,使得点 D 落在 AC 上,则 tan∠ECD 的值为 . 18. 如图,☉O 是正方形 ABCD 的内切圆,切点分别为 E,F,G,H,ED 与☉O 相交于点 M,则 sin∠MFG 的值为 . 三．解答题 19. 计算:|-3|-4sin 45°+ 8 +(π-3)0. 20. 如图,在△ABC 中,AD 是 BC 上的高,tan B=cos∠DAC. (1) 求证:AC=BD; (2)若 sin C= 12 13 ,BC=12,求 AD 的长. 21. 某体育看台侧面的示意图如图所示,观众区 AC 的坡度 i 为 1∶2,顶端 C 离水 平地面 AB 的高度为 10 m,从顶棚的 D 处看 E 处的仰角α=18°30′ ,竖直的立杆 上 C,D 两点间的距离为 4 m,E 处到观众区底端 A 处的水平距离 AF 为 3 m.求: (1)观众区的水平宽度 AB. (2)顶棚的 E 处离地面的高度 EF.(sin 18°30′ ≈0.32,tan 18°30′ ≈0.33, 结果精确到 0.1 m) 22. 图 1 是一台实物投影仪,图 2 是它的示意图,折线 B-A-O 表示固定支架,AO 垂 直水平桌面 OE 于点 O,点 B 为旋转点,BC 可转动,当 BC 绕点 B 顺时针旋转时,投影 探头 CD 始终垂直于水平桌面 OE,经测量:AO=6.8 cm,CD=8 cm,AB=30 cm,BC=35 cm. (1)如图 2,∠ABC=70°,BC∥OE. ①填空:∠BAO= °. ②求投影探头的端点 D 到桌面 OE 的距离. (2)如图 3,将(1)中的 BC 向下旋转,当投影探头的端点 D 到桌面 OE 的距离为 6 cm 时,求∠ABC 的大小.(结果精确到 0.1) (参考数据:sin 70°≈0.94,cos 20°≈0.94,sin 36.8°≈0.60,cos 53.2°≈0.60)