中考数学一轮复习知识点+题型专题讲义04 实数（教师版） 17页

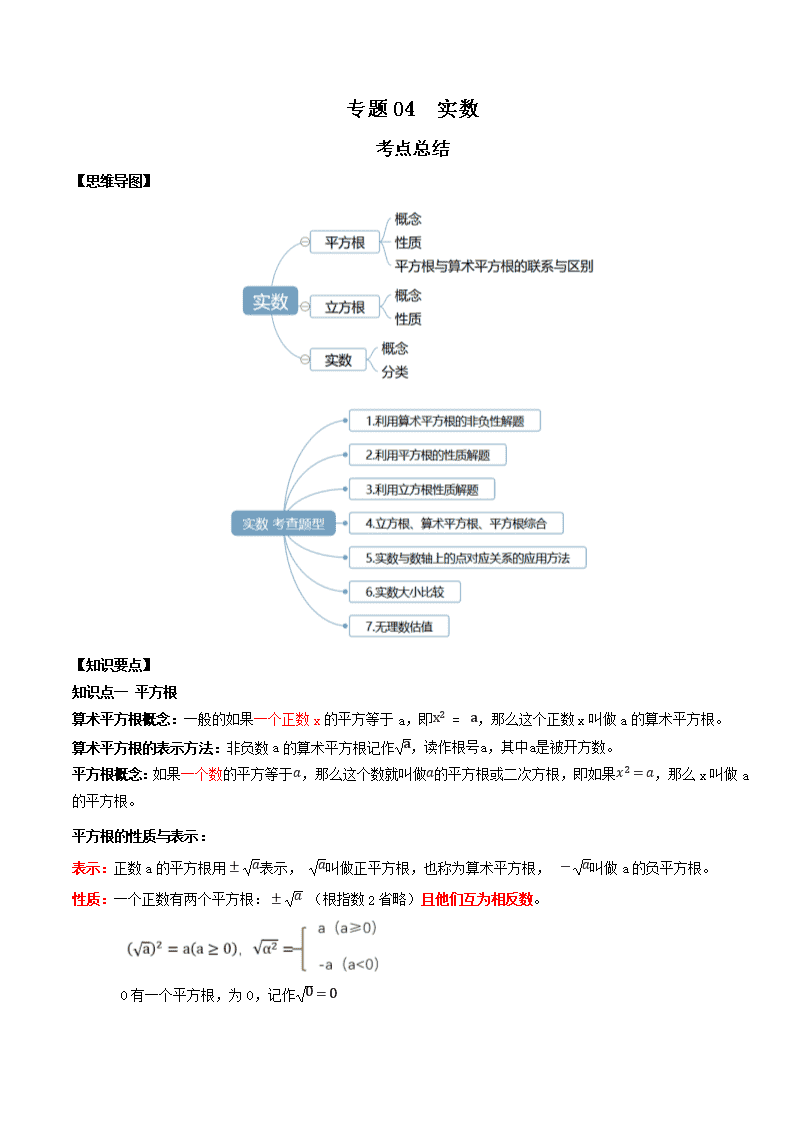
专题 04 实数 考点总结 【思维导图】 【知识要点】 知识点一 平方根 算术平方根概念：一般的如果一个正数 x 的平方等于 a，即 x 2 = a ，那么这个正数 x 叫做 a 的算术平方根。 算术平方根的表示方法：非负数 a 的算术平方根记作 a ，读作根号 a ，其中 a 是被开方数。 平方根概念：如果一个数的平方等于 ，那么这个数就叫做 的平方根或二次方根，即如果 2 = ，那么 x 叫做 a 的平方根。 平方根的性质与表示： 表示：正数 a 的平方根用 表示， 叫做正平方根，也称为算术平方根， 叫做 a 的负平方根。 性质：一个正数有两个平方根： （根指数 2 省略）且他们互为相反数。 0 有一个平方根，为 0，记作 = 负数没有平方根 平方根与算术平方根的区别与联系： 1．（2017·甘肃中考模拟）正数 9 的平方根是( ) A．3 B．±3 C． 3 D．  3 【答案】B 【详解】因为  3 的平方都等于 9，所以答案为 B 2．（2016·山东中考模拟）81 的算术平方根是（ ） A．9 B．±9 C．3 D．±3 【答案】A 【解析】 试题解析：∵92=81， ∴81 的算术平方根是 9． 故选 A． 3．（2018·江苏中考模拟）9 的算术平方根是（ ） A．﹣3 B．±3 C．3 D． 3 【答案】C 【解析】 试题分析：9 的算术平方根是 3．故选 C． 4．（2019·宁波市慈湖中学中考模拟） 16 的平方根是( ) A．﹣4 B．±2 C．±4 D．4 【答案】B 【详解】∵42＝16， ∴ 16 ＝4， ∴ 16 的平方根是±2, 故选 B． 5．（2018·河南中考模拟） 4 的算术平方根为（ ） A． 2 B． 2 C． 2 D． 2 【答案】B 【解析】 ∵ 4 =2， 而 2 的算术平方根是 2 ， ∴ 4 的算术平方根是 2 ， 故选 B． 6．（2019·浙江中考模拟） 16 的算术平方根是（ ） A．4 B．±4 C．2 D．±2 【答案】C 【详解】 16 ＝4， 4 的算术平方根是 2， 所以 16 的算术平方根是 2， 故选 C． 7．（2019·四川中考模拟） 81 的算术平方根是（ ） A．9 B．±9 C．±3 D．3 【答案】D 【详解】∵ 81 =9， 又∵（±3）2=9， ∴9 的平方根是±3， ∴9 的算术平方根是 3． 即 81 的算术平方根是 3． 故选:D． 8．（2019·黑龙江中考模拟） 9 4 的值等于（ ） A． 3 2 B． 3 2  C． 3 2  D． 81 16 【答案】A 【解析】 详解： 9 4 ＝ 3 2 ， 故选：A. 9．（2017·江苏中考真题）若方程 的两根为 和 ，且 ，则下列结论中正确的是 （ ） A． 是 19 的算术平方根 B． 是 19 的平方根 C． 是 19 的算术平方根 D． 是 19 的平方根 【答案】C 【解析】 试题分析：根据平方根的意义，可知 x-5 是 19 的一个平方根，由 a＞b，可知 a-5 是 19 的算术平方根，b-5 是其负的平方根. 故选：C 考查题型一 利用算术平方根的非负性解题 1．（2015·内蒙古中考真题）若 3 2 0,a b    则 a b的值是（ ） A．2 B 、1 C、0 D、 1 【答案】B 【解析】 试题分析：由题意得，3﹣a=0，2+b=0，解得，a=3，b=﹣2，a+b=1，故选 B． 2．（2016·山西中考模拟）若(m1)2 2n  ＝0，则 m＋n 的值是（ ） A．－1 B．0 C．1 D．2 【答案】A 【详解】∵(m1)2 2n  ＝0， ∴m−1=0，n+2=0； ∴m=1，n=−2， ∴m+n=1+(−2)=−1 故选：A. 3．（2018·山东中考模拟）已知 5a  ， 2 7b  ，且 a b a b   ，则 a b的值为（ ） A．2 或 12 B．2 或 12 C． 2 或 12 D． 2 或 12 【答案】A 【解析】 根据 a =5， 2b =7，得 a 5,b 7    ，因为 a b a b   ，则 a 5,b 7   ，则 a b =5+7=12 或-5+7=2. 故选 A. 考查题型二 利用平方根的性质解题 1．（2019·南票区九龙街道初级中学中考模拟）若 a2＝4，b2＝9，且 ab＜0，则 a﹣b 的值为（ ） A．﹣2 B．±5 C．5 D．﹣5 【答案】B 【解析】 ∵a2=4,b2=9， ∴a=±2，b=±3， ∵ab<0， ∴a=2 时,b=−3,a−b=2−(−3)=2+3=5， a=−2 时，b=3，a−b=−2−3=−5， 所以，a−b 的值为 5 或−5. 故选：B. 2．（2019·黑龙江中考模拟）对于实数 a，b 下列判断正确的是（ ） A．若 a b ，则 a b B．若 2 2a b ，则 a b C．若 2a b ，则 a b D．若 a b ，则 a b 【答案】D 【详解】解：A 也可能是 a=-b，故 A 错误；B， 2 2a b 只能说明|a|＞b，故 B 错误； C，a，b 也可能互为相反数；D，都表示算术平方根，故 D 正确； 3．（2018·江苏中考模拟）如果 a，b 分别是 2016 的两个平方根，那么 a+b﹣ab=___． 【答案】2016 【详解】∵a，b 分别是 2016 的两个平方根， ∴ 2016 2016a b  ， ， ∵a，b 分别是 2016 的两个平方根， ∴a+b=0， ∴ab=a×（﹣a）=﹣a2=﹣2016， ∴a+b﹣ab=0﹣（﹣2016）=2016， 故答案为：2016． 知识点二 立方根和开立方 立方根概念：如果一个数的立方等于 ，即 = ，那么 x 叫做 的立方根或三次方根， 表示方法：数 a 的立方根记作 ，读作三次根号 a 立方根的性质：任何实数都有唯一确定的立方根。正数的立方根是一个正数。负数的立方根是一个负数。 ０的立方根是０. 开立方概念：求一个数的立方根的运算。 开平方的表示： = = = （a 取任何数） 这说明三次根号内的负号可以移到根号外面。 注意:０的平方根和立方根都是０本身。 次方根(扩展) 概念：如果一个数的 次方（ 是大于１的整数）等于 ，这个数就叫做 的 次方根。 当 为奇数时，这个数叫做 的奇次方根。 当 为偶数时，这个数叫做 的偶次方根。 性质： 正数的偶次方根有两个： ；０的偶次方根为０： = ；负数没有偶次方根。 正数的奇次方根为正。０的奇次方根为０。负数的奇次方根为负。 1．（2019·江苏中考模拟）﹣8 的立方根是( ) A．±2 B．2 C．﹣2 D．24 【答案】C 【详解】∵23=8， ∴8 的立方根是 2， 故选 B． 2．（2018·湖南中考真题）下列各式中正确的是 ( ) A． 9 3  B．  23 3   C． 3 9 3 D． 12 3 3  【答案】D 【详解】A.原式=3，不符合题意； B.原式=|-3|=3，不符合题意； C.原式不能化简，不符合题意； D.原式=2 3 - 3 = 3 ，符合题意， 故选 D． 3．（2011·山东中考模拟） 3 8 的相反数是（ ） A．﹣2 B．2 C．﹣4 D．4 【答案】B 【详解】 3 8 的相反数是- 3 8 =2 故选 B. 4．（2019·山东中考真题）下列计算正确的是（ ） A． 2( 3) 3   B． 3 35 5  C． 36= 6 D． 0.36=-0.6 【答案】D 【详解】解：A. 2( 3) 3  ，故此选项错误； B. 3 35 5   ，故此选项错误； C. 36 6 ，故此选项错误； D. 0.36 0.6   ，正确． 故选：D． 5．（2019·湖南中考模拟）下列说法正确的是（ ） A．一个有理数的平方根有两个，它们互为相反数 B．负数没有立方根 C．无理数都是开不尽的方根数 D．无理数都是无限小数 【答案】D 【详解】（1）由平方根的性质可以得知，负有理数没有平方根，0 的平方根是 0，∴A 错误． （2）∵任何实数都有立方根，∴B 答案错误． （3）∵无理数的定义是无限不循环小数叫做无理数，∴C 答案错误． ∴D 答案正确． 故选 D． 6．（2019·浙江中考模拟）下列计算正确的是（ ） A． 16 =﹣4 B． 16 =±4 C． 2( 4) =﹣4 D． 33 ( 4) =﹣4 【答案】D 【解析】 根据二次根式的意义，可知被开方数为非负数，因此 A 不正确；根据算术平方根是平方根中带正号的，故 B 不正确；根据二次根式的性质 2 {0 a a a a    ( 0) ( 0) ( 0) a a a  ＞ ＜ 可知  24 =4，故 C 不正确；根据立方根的意 义可知  33 4 =-4，故 D 正确. 故选 D 7．（2013·广东中考模拟）一个立方体的体积为 64，则这个立方体的棱长的算术平方根为（ ） A．±4 B．4 C．±2 D．2 【答案】D 【解析】 ∵立方体的体积为 64， ∴它的棱长= 3 64=4 ， ∴它的棱长的平方根为： 2 . 故选 D. 8．（2019·来宾市第四中学中考模拟）下列说法①﹣5 的绝对值是 5；②﹣1 的相反数是 1；③0 的倒数是 0； ④64 的立方根是±4，⑤ 1 3 是无理数，⑥4 的算术平方根是 2，其中正确的个数为（ ） A．2 B．3 C．4 D．5 【答案】B 【详解】①﹣5 的绝对值是 5，正确；②﹣1 的相反数是 1，正确；③0 没有倒数，错误；④64 的立方根是 4， 错误，⑤ 1 3 不是无理数，是有理数，错误，⑥4 的算术平方根是 2，正确， 故选 B． 考查提醒三 利用立方根的性质解题 1．下列各组数中互为相反数的是（ ） A．－2 与 2（-2) B．－2 与 3 8 C．2 与（- 2 ）2 D．|- 2 |与 2 【答案】A 【解析】 选项 A. －2 与 22)（ =2， 选项 B. －2 与 3 8 =-2， 选项 C. 2 与（- 2 ）2=2, 选项 D. |- 2 |= 2 与 2 , 故选 A. 2.（2018·福建中考模拟）若实数 x y， 满足 2(2 3) 9 4 0x y    ，则 xy 的立方根为__________． 【答案】 3 2  【详解】由题意得：2x-3=0，9+4y=0， 解得：x= 3 2 ，y= 9 4  ， ∴xy= 27 8  ， ∴xy 的立方根是 3 2  ， 故答案为： 3 2  . 考查题型四 立方根、算术平方根、平方根的综合 1．（2018·合肥市第四十五中学初一期中）已知 a+3 和 2a﹣15 是某正数的两个平方根，b 的立方根是﹣2，c 算术平方根是其本身，求 2a+b﹣3c 的值． 【答案】当 a＝4，b＝﹣8，c＝0，2a+b﹣3c＝0；当 a＝4，b＝﹣8，c＝1，2a+b﹣3c＝﹣3． 【详解】∵某正数的两个平方根分别是 a+3 和 2a﹣15，b 的立方根是﹣2．c 算术平方根是其本身 ∴a+3+2a﹣15＝0，b＝﹣8，c＝0 或 1， 解得 a＝4． 当 a＝4，b＝﹣8，c＝0，2a+b﹣3c＝8﹣8﹣0＝0； 当 a＝4，b＝﹣8，c＝1，2a+b﹣3c＝8﹣8﹣3＝﹣3． 2．已知 知 的算术平方根是 4， 知 晦 的立方根是 2 ，求 知 的平方根． 【答案】 【详解】根据题意得： x 知 = ， x 知 y 晦 = ， 解得： x = ， y = ， 则 x 知 y = 知 = ㌳ ，9 的平方根为 ． 所以 x 知 y 的平方根为 ． 3.已知 2 1a  的算术平方根足3，3 1a b  的立方根是 2 ，求 2a b 的平方根． 【答案】± 17 【详解】解：由题意得：2a-1=9，3a+b-1=8， 解得：a=5，b=-6， 则 a-2b=5-2×(-6)=17，17 的平方根是± 17 4.已知 a+1 的算术平方根是 1，﹣27 的立方根是 b﹣12，c﹣3 的平方根是±2，求 a+b+c 的平方根． 【答案】±4． 【详解】解：∵a+1 的算术平方根是 1， ∴a+1=1，即 a=0； ∵﹣27 的立方根是 b﹣12， ∴b﹣12=﹣3，即 b=9； ∵c﹣3 的平方根是±2， ∴c﹣3=4，即 c=7； ∴a+b+c=0+9+7=16， 则 a+b+c 的平方根是±4． 5．（2019·贵州省毕节梁才学校初二期中）已知 2x  是49的算术平方根，2 10x y  的立方根是2，求 2 2x y 的平方根． 【答案】±13． 【详解】解：∵x+2 是 49 的算术平方根， ∴x+2=7， 解得 x=5， ∵ 2 10x y  的立方根是 2， ∴ 2 10x y  =8， 解得 y=12， ∴ 2 2x y = 2 25 12 =169， ∵（±13）2=169， ∴ 2 2x y 的平方根是±13． 知识点三 实数 无理数的概念：无限不循环小数叫做无理数。 实数概念：有理数和无理数统称为实数 实数的分类： 1.按属性分类： 2.按符号分类 实数和数轴上的点的对应关系（重点）： 实数和数轴上的点一一对应，即每一个实数都可以用数轴上的一个点表示．数轴上的每一个点都可以表示 一个实数． 2 的画法：画边长为 1 的正方形的对角线 在数轴上表示无理数通常有两种情况： 1.尺规可作的无理数，如 2 2.尺规不可作的无理数 ，只能近似地表示，如π，1.010010001…… 实数大小比较的方法（常用）：1）平方法 2）根号法 3）求差法 实数的三个非负性及性质： 1.在实数范围内，正数和零统称为非负数。 2.非负数有三种形式 ①任何一个实数 a 的绝对值是非负数，即|a|≥0； ②任何一个实数 a 的平方是非负数，即 2 ≥0； ③任何非负数的算术平方根是非负数，即 ≥0 3.非负数具有以下性质 ①非负数有最小值零； ②非负数之和仍是非负数； ③几个非负数之和等于 0，则每个非负数都等于 0 1．（2019·四川中考模拟）下列实数 0， 2 3 ， 3 ，π，其中，无理数共有（ ） A．1 个 B．2 个 C．3 个 D．4 个 【答案】B 【详解】解：无理数有： 3 ， π. 故选 B. 2．（2013·贵州中考真题）下列各数中，3 14159， 3 8， 131131113 ， ， 25， 1 7 ，无理数的个数 有（ ） A．1 个 B．2 个 C．3 个 D．4 个 【答案】B 【解析】 试题分析：无限不循环小数为无理数，由此可得出无理数的个数，因此，由定义可知无理数有：0.131131113…， ﹣π，共两个。故选 B。 3．（2018·山东中考真题）下列各数：-2，0， 1 3 ，0.020020002…， ， 9 ，其中无理数的个数是（ ） A．4 B．3 C．2 D．1 【答案】C 【解析】 2 是有理数，0 是有理数， 1 3 是有理数，0.020020002…是无理数， 是无理数， 9 是有理数，所以无理 数有 2 个，故选 C. 4．（2019·山东中考模拟）在实数 5 ，22 7 ，π﹣2， 3 27 ，0.121 221 222 1…（两个”1”之间依次多一个“2”） 中，有理数有（ ） A．1 个 B．2 个 C．3 个 D．4 个 【答案】B 【详解】 22 7 ， 3  27 =-3 是有理数； 5 ，π﹣2，0.121 221 222 1…（两个”1”之间依次多一个“2”）是无理数. 故选 B. 5．（2018·贵州中考模拟）下列说法： ①  210 10   ； ②数轴上的点与实数成一一对应关系； ③﹣2 是 16 的平方根； ④任何实数不是有理数就是无理数； ⑤两个无理数的和还是无理数； ⑥无理数都是无限小数， 其中正确的个数有( ) A．2 个 B．3 个 C．4 个 D．5 个 【答案】C 【详解】①∵  210 10  ，∴  210 10   是错误的； ②数轴上的点与实数成一一对应关系，故说法正确； ③∵ 16 ＝4，故-2 是 16 的平方根，故说法正确； ④任何实数不是有理数就是无理数，故说法正确； ⑤两个无理数的和还是无理数，如 2 和 2 是错误的； ⑥无理数都是无限小数，故说法正确； 故正确的是②③④⑥共 4 个； 故选 C. 6．（2018·四川中考模拟） 2( 2) 的相反数是（ ） A．2 B．﹣2 C．4 D．﹣ 2 【答案】A 【解析】  2 2 的相反数是 2 2 ，即 2. 故选 A. 7．（2018·山东中考模拟）1﹣ 2 的相反数是（ ） A．1﹣ 2 B． 2 ﹣1 C． 2 D．﹣1 【答案】B 【详解】根据 a 的相反数为-a 即可得，1﹣ 2 的相反数是 2 ﹣1. 故选 B. 8．（2018·黑龙江中考模拟）实数 3 的绝对值是 ( ) A．3 B． 3 C． 3 D． 3 3  【答案】B 【详解】解： 3 = 3 故选 B. 9．（2018·四川中考模拟） 3 2 的绝对值是（ ） A． 3 2 B． 3 2 C． 2 3 D． 3 2  【答案】C 【解析】 ∵ 3 2 0  ， ∴  3 2 = 3 2 =2 3    . 故选 C. 考查题型五 实数与数轴上的点的对应关系的应用方法 1．（2013·湖北中考模拟）实数 a、b 在数轴上的位置如图所示，且|a|＞|b|，则化简 2a a b  的结果为（ ） A．2a+b B．-2a+b C．b D．2a-b 【答案】C 【解析】 ∵由数轴可知，b＞0＞a，且 |a|＞|b|， ∴  2a a b a a b b       . 故选 C． 2．（2013·广西中考模拟）如图，数轴上点 P 表示的数可能是（ ）. A． B． C． D． 2【答案】B 【详解】由图象可知，2＜p＜3． ∵ 2.236，∴数轴上点 P 表示的数可能是 ． 故选 B． 3．（2018·天津中考模拟）在如图所示的数轴上，点 B 与点 C 关于点 A 对称，A、B 两点对应的实数分别是 3 和﹣1，则点 C 所对应的实数是( ) A．1+ 3 B．2+ 3 C．2 3 ﹣1 D．2 3 +1 【答案】D 【详解】设点 C 所对应的实数是 x．根据中心对称的性质，对称点到对称中心的距离相等，则有  x 3= 3 1   ，解得 x=2 3+1. 故选 D. 考查题型六 实数大小比较 1．（2018·湖南中考模拟） 2 6 、 27 、5 三个数的大小关系是（ ） A． 2 6 5 27  B． 27 5 2 6  C． 2 6 27 5  D． 27 2 6 5  【答案】A 【详解】这一组数据可化为 24 、 27 、 25 ． ∵27＞25＞24，∴ 27 ＞ 25 ＞ 24 ，即 2 6 ＜5＜ 27 ． 故选 A． 2.（2018·天津中考模拟）比较 32 5 7， ， 的大小，正确的是( ) A． 3 7 2 5  B． 32 5 7  C． 32 7 5  D． 35 7 2  【答案】A 【详解】∵2 4 5 ＜ ，∴2 5＜ ； ∵ 3 37 8 2＜ ，∴ 3 7 2＜ ，∴ 3 7 2 5＜ ＜ ． 故选 A． 3．（2019·天津中考模拟）若 a 30 ， b 6  ， 3c 65 则下列关系正确的为( ) A． a b c  B． c b a  C． b a c  D． b c a  【答案】C 【详解】∵25<30<36， ∴5< 30 <6，即 5a>c， 故选 C. 考查题型七 无理数估算方法 1.（2019·辽宁中考模拟）估计 5 6 ﹣ 24 的值应在（ ） A．5 和 6 之间 B．6 和 7 之间 C．7 和 8 之间 D．8 和 9 之间 【答案】C 【详解】5 6 ﹣ 24 =5 6 2 6 3 6= 54  ， ∵49<54<64， ∴7< 54 <8， ∴5 6 ﹣ 24 的值应在 7 和 8 之间， 故选 C． 2.（2019·天津中考模拟）3+ 10 的结果在下列哪两个整数之间（ ） A．6 和 7 B．5 和 6 C．4 和 5 D．3 和 4 【答案】A 【详解】解：∵3＜ 10 ＜4， ∴6＜3+ 10 ＜7， 故选：A． 3．（2018·海南中考模拟）若 m 27 2  ，则估计 m 的值所在范围是 ( ) A．1 m 2  B． 2 m 3  C．3 m 4  D． 4 m 5  【答案】C 【详解】因为，5 27 6  , 所以，3 27 2 4   , 即3 m 4  故选 C