2021中考数学复习微专题 几何图形必考综合题型突破与提升专练(有答案） 14页

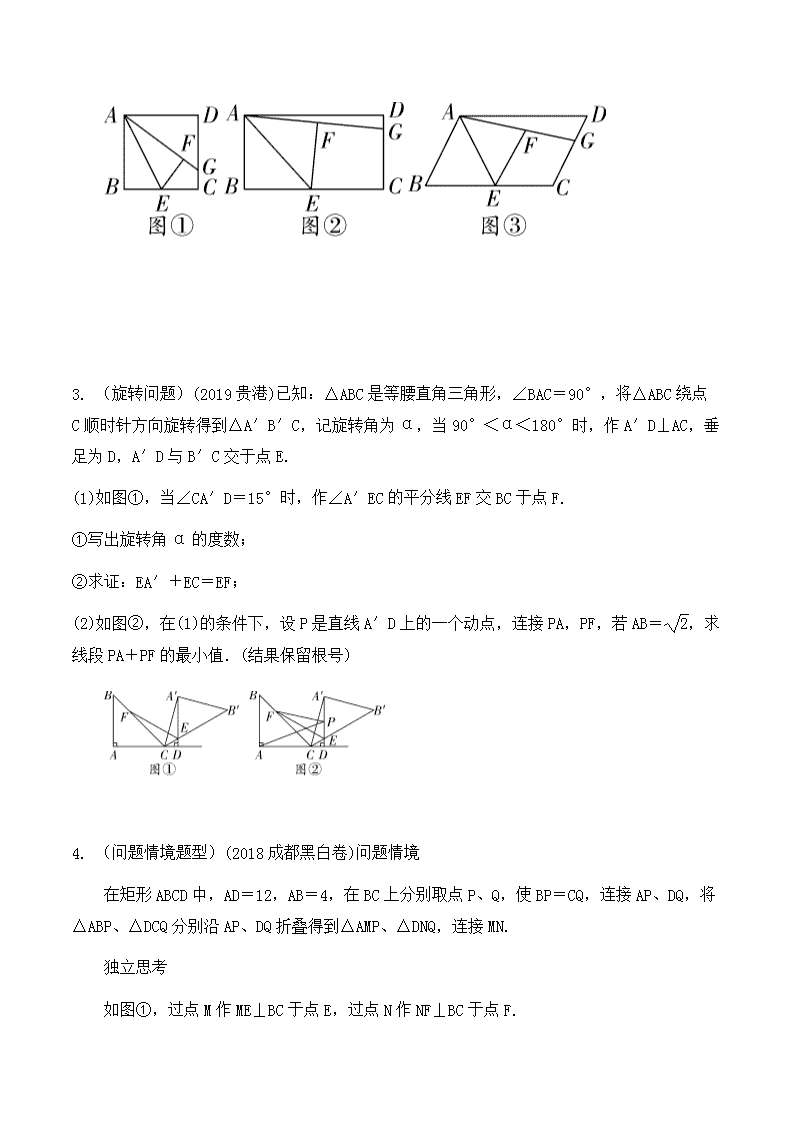
中考数学复习微专题：几何图形必考综合题型突破与提升专练 1. 动点问题(2019 衢州)如图，在 Rt△ABC 中，∠C＝90°，AC＝6，∠BAC＝60°，AD 平分∠BAC 交 BC 于点 D，过点 D 作 DE∥AC 交 AB 于点 E.点 M 是线段 AD 上的动点，连接 BM 并延长分别交 DE，AC 于点 F，G. (1)求 CD 的长； (2)若点 M 是线段 AD 的中点，求EF DF 的值； (3)请问当 DM 的长满足什么条件时，在线段 DE 上恰好只有一点 P，使得∠CPG＝60°？ 2. （图形形状变化问题） (2017 成都黑白卷)如图，在正方形 ABCD 中，点 E 是 BC 的中点， 将△ABE 沿 AE 折叠后得到△AFE，点 F 在正方形 ABCD 的内部，延长 AF 交 CD 于点 G. (1)猜想并证明线段 FG 与 CG 的数量关系； (2)若将图①中的正方形改成矩形，其他条件不变，如图②，那么线段 FG 与 CG 之间的数量关 系是否改变？请证明你的结论； (3)若将图①中的正方形改成平行四边形，其他条件不变，如图③，那么线段 FG 与 CG 之间的 数量关系是否会改变？请证明你的结论． 3. （旋转问题）(2019 贵港)已知：△ABC 是等腰直角三角形，∠BAC＝90°，将△ABC 绕点 C 顺时针方向旋转得到△A′B′C，记旋转角为α，当 90°＜α＜180°时，作 A′D⊥AC，垂足 为 D，A′D 与 B′C 交于点 E. (1)如图①，当∠CA′D＝15°时，作∠A′EC 的平分线 EF 交 BC 于点 F. ①写出旋转角α的度数； ②求证：EA′＋EC＝EF； (2)如图②，在(1)的条件下，设 P 是直线 A′D 上的一个动点，连接 PA，PF，若 AB＝ 2，求 线段 PA＋PF 的最小值．(结果保留根号) 4. （问题情境题型）(2018 成都黑白卷)问题情境 在矩形 ABCD 中，AD＝12，AB＝4，在 BC 上分别取点 P、Q，使 BP＝CQ，连接 AP、DQ，将 △ABP、△DCQ 分别沿 AP、DQ 折叠得到△AMP、△DNQ，连接 MN. 独立思考 如图①，过点 M 作 ME⊥BC 于点 E，过点 N 作 NF⊥BC 于点 F. (1)求证：ME＝NF； (2)试探究线段 MN 与 BC 满足的位置关系，并说明理由； (3)若 BP＝3，求 MN 的长； 拓展延伸 (4)如图②，当点 P 与点 Q 重合时，直接写出 MN 的长． 5. （几何探究类问题）(2018 成都黑白卷)如图，在△ABC 中，AB＝AC，过点 C 作 CG⊥BA，交 BA 的延长线于点 G，将一等腰三角尺的一条直角边与 AC 在同一直线上，该三角尺的直角顶点 为 F. (1)如图①，当另一条直角边恰好经过点 B 时，求证 BF＝CG； (2)将三角尺沿 AC 方向平移到图②位置时，另一条直角边交 BC 于点 D，过点 D 作 DE⊥BA 于点 E，试探究线段 DE、DF 与 CG 之间满足的等量关系，并说明理由； (3)如图③，将三角尺继续沿 AC 方向平移(点 F 不与点 C 重合)时，若 AG∶AB＝5∶13，BC＝4 13， 求 DE＋DF 的值． 参考答案 1. 解：(1)∵AD 平分∠BAC，∠BAC＝60°， ∴∠DAC＝1 2∠BAC＝30°. 在 Rt△ADC 中，DC＝AC·tan30°＝2 3； (2)∵∠BAC＝60°， ∴在 Rt△ABC 中，BC＝AC· tan∠BAC＝6 3， ∴BD＝BC－DC＝4 3. ∵DE∥AC， ∴∠EDA＝∠DAC，∠DFM＝∠AGM. ∵AM＝DM， ∴△DFM≌△AGM(AAS)， ∴DF＝AG. ∵DE∥AC， ∴△BFE∽△BGA，△BDE∽△BCA. ∴EF AG＝BE BA＝BD BC， ∴EF DF ＝EF AG ＝BD BC ＝4 3 6 3 ＝2 3 ； (3)过 C，P，G 作外接圆，圆心为 Q， ∵∠CPG＝60°， ∴△CQG 是顶角为 120°的等腰三角形． ①当⊙Q 与 DE 相切时，如解图①，过 Q 点作 QH⊥AC 于点 H，并延长 HQ 与 DE 交于点 P， 连接 QC，QG. 设⊙Q 的半径 QP＝r， 则 QH＝1 2 r，PH＝r＋1 2 r＝CD＝2 3， 解得 r＝4 3 3 ， ∴CG＝2CH＝2QC·cos30°＝2×4 3 3 × 3 2 ＝4，∴AG＝2. ∵DE∥AC， ∴∠EDA＝∠DAC， 又∵∠DMP＝∠AMG， ∴△DFM∽△AGM， ∴DM AM ＝DF AG ＝4 3 ，则DM AD ＝4 7 . 由(1)可得 DC＝2 3， ∴在 Rt△ACD 中，AD＝2CD＝4 3， ∴DM＝16 3 7 ； 第 1 题解图① ②当⊙Q 经过点 E 时，如解图②，过 C 点作 CK⊥AB，垂足为 K. 设⊙Q 的半径 QC＝QE＝r， ∵AC＝6，∠BAC＝60°，CK＝AC·sin∠BAC＝3 3，AK＝AC·cos∠BAC＝3， ∴QK＝3 3－r. ∵AE＝ CD sin∠BAC ＝4， ∴EK＝AE－AK＝1. ∴在 Rt△EQK 中，12＋(3 3－r)2＝r2，解得 r＝14 3 9 ， ∴CG＝2×14 3 9 × 3 2 ＝14 3 . ∵△DFM∽△AGM， ∴同(3)①得 DM＝14 3 5 ； 第 1 题解图② ③当⊙Q 经过点 D 时，如解图③，此时点 M 与点 G 重合，且恰好在点 A 处，可得 DM＝2CD ＝4 3. ∴综上所述，当 DM＝16 3 7 或14 3 5