数学华东师大版九年级上册教案23-2 相似图形 3页

1 23.2 相似图形 教学目标 1.了解相似多边形和相似比的概念； 2.会根据条件判断两个多边形是否为相似多边形； 3.掌握相似多边形的性质，能根据相似比进行相关的计算. 教学重难点 【教学重点】 相似多边形和相似比的概念，根据条件判断两个多边形是否为相似多边形. 【教学难点】 相似多边形的性质，能根据相似比进行相关的计算. 课前准备 无 教学过程 一、情景导入 观察以下三组图形，每一组图形的对应边、对应角有什么关系呢？ 二、合作探究 探究点一：相似多边形的判定 下列图形都相似吗？为什么？ （1）所有正方形；（2）所有矩形；（3）所有菱形；（4）所有等边三角形；（5）所有等腰三 角形；（6）所有等腰梯形；（7）所有等腰直角三角形；（8）所有正五边形. 解析：利用定义判断边数相同的多边形是否相似，要从两方面进行判断：（1）对应角相等； （2）对应边成比例，两者缺一不可. 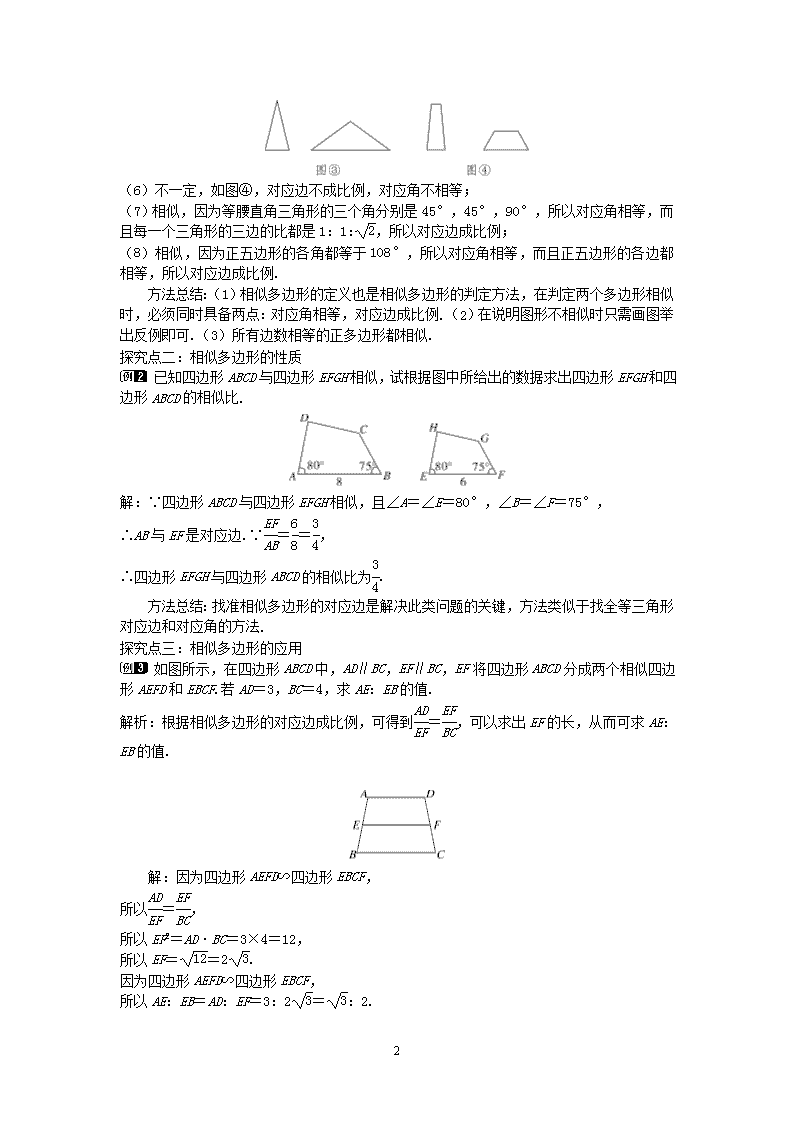解：（1）相似，因为正方形每个角都等于 90°，所以对应角相等，而每个正方形的边长都 相等，所以对应边成比例； （2）不一定，虽然矩形的每个角都等于 90°，对应角相等，但是对应边不一定成比例，如 图①； （3）不一定，每个菱形的四条边长都相等，所以两菱形的对应边一定成比例，但是它们的 对应角不一定相等，如图②，显然两个菱形的对应角是不相等的； （4）相似，因为每个等边三角形的三条边都相等，所以两个等边三角形的对应边一定成比 例，并且对应角都等于 60°； （5）不一定，如图③，对应边不成比例，对应角不相等； 2 （6）不一定，如图④，对应边不成比例，对应角不相等； （7）相似，因为等腰直角三角形的三个角分别是 45°，45°，90°，所以对应角相等，而 且每一个三角形的三边的比都是 1：1： 2，所以对应边成比例； （8）相似，因为正五边形的各角都等于 108°，所以对应角相等，而且正五边形的各边都 相等，所以对应边成比例. 方法总结：（1）相似多边形的定义也是相似多边形的判定方法，在判定两个多边形相似 时，必须同时具备两点：对应角相等，对应边成比例.（2）在说明图形不相似时只需画图举 出反例即可.（3）所有边数相等的正多边形都相似. 探究点二：相似多边形的性质 已知四边形 ABCD 与四边形 EFGH 相似，试根据图中所给出的数据求出四边形 EFGH 和四 边形 ABCD 的相似比. 解：∵四边形 ABCD 与四边形 EFGH 相似，且∠A＝∠E＝80°，∠B＝∠F＝75°， ∴AB 与 EF 是对应边.∵EF AB ＝6 8 ＝3 4 ， ∴四边形 EFGH 与四边形 ABCD 的相似比为3 4 . 方法总结：找准相似多边形的对应边是解决此类问题的关键，方法类似于找全等三角形 对应边和对应角的方法. 探究点三：相似多边形的应用 如图所示，在四边形 ABCD 中，AD∥BC，EF∥BC，EF 将四边形 ABCD 分成两个相似四边 形 AEFD 和 EBCF.若 AD＝3，BC＝4，求 AE：EB 的值. 解析：根据相似多边形的对应边成比例，可得到AD EF ＝EF BC ，可以求出 EF 的长，从而可求 AE： EB 的值. 解：因为四边形 AEFD∽四边形 EBCF， 所以AD EF ＝EF BC ， 所以 EF2＝AD·BC＝3×4＝12， 所以 EF＝ 12＝2 3. 因为四边形 AEFD∽四边形 EBCF， 所以 AE：EB＝AD：EF＝3：2 3＝ 3：2. 3 方法总结：若两个多边形相似，则它们对应的边成比例，根据此特性，可列等式或比例 式求解. 在 AB＝20m，AD＝30m 的矩形花坛 ABCD 的四周建筑小路. （1）如果四周的小路的宽均相等，如图①，那么小路四周所围成的矩形 A′B′C′D′和矩 形 ABCD 相似吗？请说明理由； （2）如果对应着的两条小路的宽均相等，如图②，试问小路的宽 x 与 y 的比值是多少时， 能使小路四周所围成的矩形 A′B′C′D′和矩形 ABCD 相似？ 解析：（1）根据两矩形的对应边是否成比例来判断两矩形是否相似； （2）根据矩形相似的条件列出等量关系式，从而求出 x 与 y 的比值. 解：（1）矩形 A′B′C′D′和矩形 ABCD 不相似.理由如下： 假设两个矩形相似，不妨设小路宽为 xm， 则30＋2x 30 ＝20＋2x 20 ，解得 x＝0. ∵由题意可知，小路宽不可能为 0， ∴矩形 A′B′C′D′和矩形 ABCD 不相似； （2）当 x 与 y 的比值为 3：2 时，小路四周所围成的矩形 A′B′C′D′和矩形 ABCD 相似. 理由如下： 若矩形 A′B′C′D′和矩形 ABCD 相似， 则30＋2x 30 ＝20＋2y 20 ，所以x y ＝3 2 . ∴当 x 与 y 的比值为 3：2 时，小路四周所围成的矩形 A′B′C′D′和矩形 ABCD 相似. 方法总结：因为矩形的四个角均是直角，所以在有关矩形相似的问题中，只需看对应边 是否成比例，若成比例，则相似，否则不相似. 三、板书设计 相似多边形 相似多边形：各角分别相等、各边 成比例的两个多边形 相似比：相似多边形对应边的比 性质：相似多边形的对应角相等，对 应边成比例 判定：各角分别相等，各边成比例， 二者缺一不可 四、教学反思 在探索相似多边形本质特征的过程中，让学生运用“观察－比较－猜想”分析问题，进一步 发展学生观察、分析、判断、归纳、类比、反思、交流等方面的能力，提高数学思维水平， 体会反例的作用，培养与他人交流、合作的意识和品质.