- 357.50 KB
- 2021-11-11 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
1.2 二次函数的图象
第1课时 二次函数y=ax2(a≠0)的图象及特征
知识点 二次函数y=ax2(a≠0)的图象及特征
二次函数y=ax2(a≠0)的图象是一条____________________________________________,
它的对称轴是________,图象的顶点坐标是________.当a>0时,抛物线开口________;当a<0时,抛物线开口________.
1.用描点法画二次函数图象的一般步骤:
(1)________;(2)________;(3)________.
2.(1)在同一直角坐标系中,画出下列函数的图象:
①y=x2;②y=-x2.
(2)根据(1)中所画的函数图象完成下列表格.
二次函数
图象的开口
方向
图象的对
称轴
图象的顶点
坐标
5
y=x2
y=-x2
类型 y=ax2型二次函数图象的特征
例1 [教材例1针对练] 已知二次函数y=ax2(a≠0)的图象经过点(1,-3).
(1)求a的值,并写出这个二次函数的表达式;
(2)你能说出这条抛物线的哪些特征(至少三条)?
【归纳总结】二次函数y=ax2(a≠0)的图象的特征
(1)图象是一条抛物线.
(2)对称轴是y轴,顶点是坐标原点.
(3)当a>0时,抛物线的开口向上,顶点是抛物线的最低点;当a<0时,抛物线的开口向下,顶点是抛物线的最高点.
[拓展] |a|越大,抛物线的开口越小;|a|相等时,抛物线的形状相同.
5
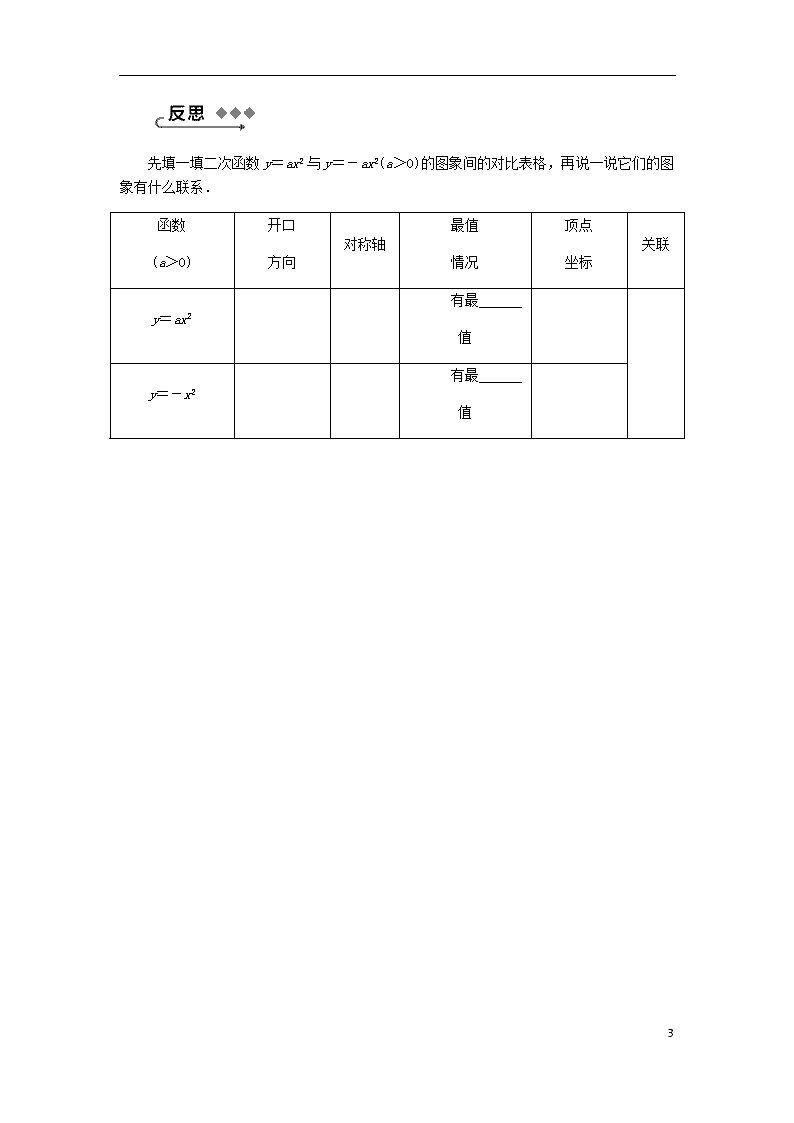
先填一填二次函数y=ax2与y=-ax2(a>0)的图象间的对比表格,再说一说它们的图象有什么联系.
函数
(a>0)
开口
方向
对称轴
最值
情况
顶点
坐标
关联
y=ax2
有最
值
y=-x2
有最
值
5
详解详析
【学知识】
知识点 抛物线 y轴 (0,0) 向上 向下
1.[答案] 列表 描点 连线
2.[解析] (1)按照画函数图象的步骤:列表、描点、连线便可正确画出图象,而二次函数y=ax2(a≠0)中自变量x的取值范围是全体实数,且它的图象关于y轴对称,所以列表时为了计算与描点方便,可以“0”为中心选x的值,尽可能取整数且不宜太大.(2)根据(1)中所画的函数图象填表即可.
解:(1)①列表如下:
x
…
-3
-2
-1
0
1
2
3
…
y=x2
…
3
0
3
…
②列表如下:
x
…
-3
-2
-1
0
1
2
3
…
y=-x2
…
-3
-
-
0
-
-
-3
…
描点、连线如图所示.
(2)填表如下:
二次函数
图象的开
图象的
图象的顶
5
口方向
对称轴
点坐标
y=x2
上
y轴
(0,0)
y=-x2
下
y轴
(0,0)
【筑方法】
例1 解:(1)把(1,-3)代入y=ax2得a=-3,所以这个二次函数的表达式为y=-3x2.
(2)答案不唯一,如开口向下,对称轴是y轴,顶点为坐标原点等.
【勤反思】
[小结] y轴 (0,0) 开口向上 开口向下 越小
[反思]
函数
(a>0)
开口
方向
对称轴
最值
情况
顶点
坐标
关联
y=ax2
向上
y轴
有最
小__值
(0,0)
①关于x轴
对称;
②形状相同
y=-ax2,向下,y轴,有最大值,(0,0)
5
相关文档
- 初中数学中考复习课件章节考点专题2021-11-1121页
- 初中数学中考复习课件章节考点专题2021-11-1136页
- 2020届初中物理章节复习 第11章 功2021-11-1118页
- 2020届初中物理章节复习 第17章 欧2021-11-119页
- 初中数学中考复习课件章节考点专题2021-11-1136页
- 2020届初中生物中考一轮复习考点测2021-11-114页
- 2020秋初中《道德与法治》知识点归2021-11-1128页
- 初中中考物理复习课件:第18讲 电功2021-11-1166页
- 初中地理复习专题 中国地理 陕南地2021-11-118页
- 普兰店市 17届 初中毕业升学考试试2021-11-116页