2019年辽宁锦州中考真题数学试卷 7页

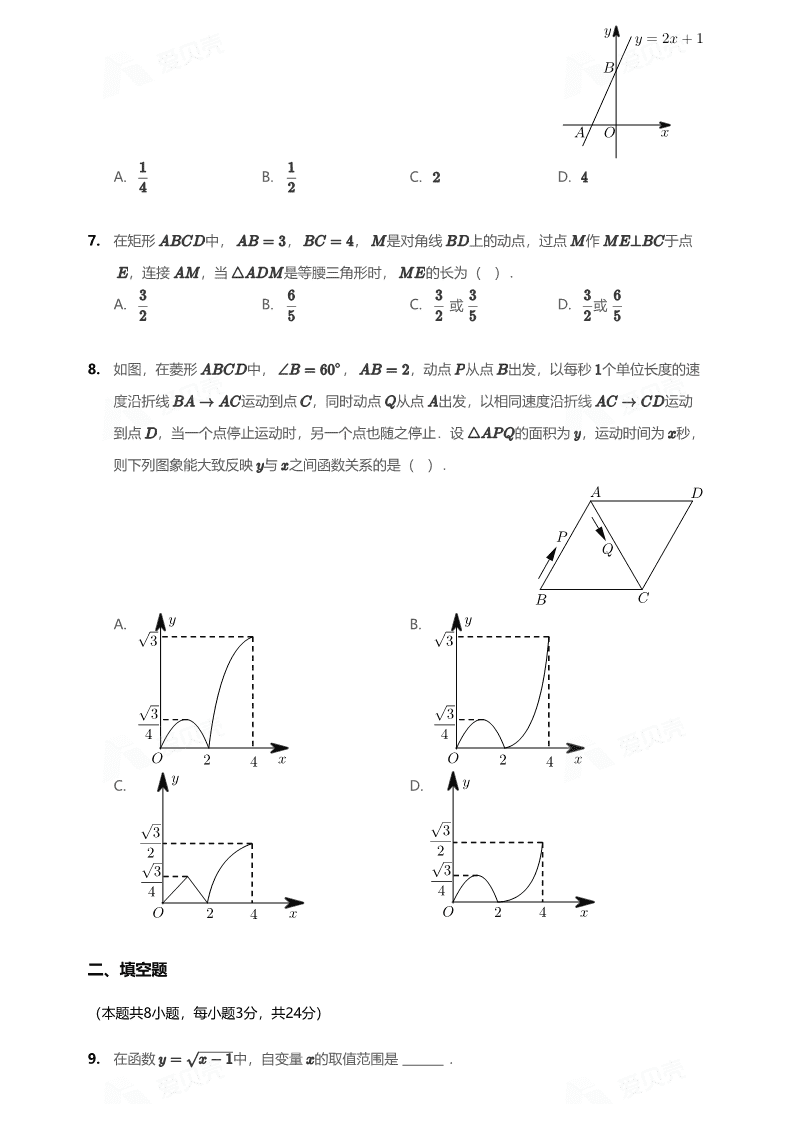
/ 2019年辽宁锦州中考真题数学试卷 一、选择题 （本题共8小题，每小题2分，共16分） 1. A. B. C. D. 的相反数是（ ）． 2. A. B. C. D. 下列既是轴对称图形又是中心对称图形的是（ ）． 3. A. 甲 B. 乙 C. 丙 D. 丁 甲、乙、丙、丁四名同学进行跳高测试，每人 次跳高成绩的平均数都是 ，方差分别是 ， ， ， ，则这四名同学跳高成绩最稳定的是（ ）． 甲 乙 丙 丁 4. A. B. C. D. 下列运算正确的是（ ）． 5. A. B. C. D. 如图， 与 交于点 ， ， ， ，则 的度数为（ ）． 6. 如图，一次函数 的图象与坐标轴分别交于 ， 两点， 为坐标原点，则 的 面积为（ ）． / A. B. C. D. 7. A. B. C. 或 D. 或 在矩形 中， ， ， 是对角线 上的动点，过点 作 于点 ，连接 ，当 是等腰三角形时， 的长为（ ）． 8. A. B. C. D. 如图，在菱形 中， ， ，动点 从点 出发，以每秒 个单位长度的速 度沿折线 运动到点 ，同时动点 从点 出发，以相同速度沿折线 运动 到点 ，当一个点停止运动时，另一个点也随之停止．设 的面积为 ，运动时间为 秒， 则下列图象能大致反映 与 之间函数关系的是（ ）． 二、填空题 （本题共8小题，每小题3分，共24分） 9. 在函数 中，自变量 的取值范围是 ． / 10. 为了落实“优化税收营商环境，助力经济发展和民生改善”的政策，国家税务总局统计数据显 示， 年 至 月合计减税 亿元，将 亿元用科学记数法表示为 元． 11. 在一个不透明的袋子中装有 个白球和若干个红球，这些球除颜色外都相同．每次从袋子中随机 摸出一个球，记下颜色后再放回袋中，通过多次重复试验发现摸出红球的频率稳定在 附近， 则袋子中红球约有 个． 12. 如图，正六边形 内接于⊙ ，边长 ，则扇形 的面积为 ． 13. 甲、乙两地相距 ，如果乘高铁列车从甲地到乙地比乘特快列车少用 ，已知高铁列车的 平均速度是特快列车的 倍，设特快列车的平均速度为 ，根据题意可列方程 为 ． 14. 如图，将一个含 角的三角尺 放在直角坐标系中，使直角顶点 与原点 重合，顶点 ， 分别在反比例函数 和 的图象上，则 的值为 ． 15. 如图，在矩形 中， ， ， 是 边的中点， 是 边上的动点，将 沿 所在直线折叠，得到 ，连接 ，则 的最小值是 ． / 16. 如图，边长为 的等边 ， 边在 轴上，点 在 轴的正半轴上，以 为边作等边 ，边 与 交于点 ，以 为边作等边 ，边 与 交于点 ， 为边作等边 ，边 与 交于点 依此规律继续作等边 ，记 的面积为 ， 的面积为 ， 的面积为 的面积为 ，则 ，( ，且 为整数）. 三、解答题 （本题共9小题，共80分） 17. 先化简，再求值： ，其中 ﹒． 18. （ 1 ） （ 2 ） （ 3 ） 为了响应“学习强国，阅读兴辽”的号召，某校鼓励学生利用课余时间广泛阅读，学校打算购进 一批图书．为了解学生对图书类别的喜欢情况，校学生会随机抽取部分学生进行问卷调查，规定 被调查学生从“文学、历史、科学、生活”中只选择自己最喜欢的一类，根据调查结果绘制了下 面不完整的统计图． 文学 历史 科学 生活 类别 人数 文学 生活 历史 科学 请根据图表信息，解答下列问题． 此次共调查了学生 人． 请通过计算补全条形统计图． 若该校共有学生 人，请估计这所学校喜欢“科学”类书的学生人数． 19. / （ 1 ） （ 2 ） 对垃圾进行分类投放，能提高垃圾处理和再利用的效率，减少污染，保护环境．为了检查垃圾分 类的落实情况，某居委会成立了甲、乙两个检查组，采取随机抽查的方式分别对辖区内的 ， ， ， 四个小区进行检查，并且每个小区不重复检查． 甲组抽到 小区的概率是 ． 请用列表或画树状图的方法求甲组抽到 小区，同时乙组抽到 小区的概率． 20. （ 1 ） （ 2 ） 某市政部门为了保护生态环境，计划购买 ， 两种型号的环保设备．已知购买一套 型设备和 三套 型设备共需 万元，购买三套 型设备和两套 型设备共需 万元． 求 型设备和 型设备的单价各是多少万元． 根据需要市政部门采购 型和 型设备共 套，预算资金不超过 万元，问最多可购 买 型设备多少套？ 21. 如图，某学校体育场看台的顶端 到地面的垂直距离 为 ，看台所在斜坡 的坡比 ，在点 处测得旗杆顶点 的仰角为 ，在点 处测得旗杆顶点 的仰角为 ，且 ， ， 三点在同一水平线上，求旗杆 的高度．（结果精确到 ，参考数据： ， ） 22. （ 1 ） （ 2 ） 如图， ， 是以 为直径的⊙ 上的点，且 ，弦 交 于点 ， 平分 ， 于点 ． 求证： 是⊙ 的切线． 若 ， ，求 的长． 23. / （ 1 ） （ 2 ） （ 3 ） 年在法国举办的女足世界杯，为人们奉献了一场足球盛宴．某商场销售一批足球文化衫，已 知该文化衫的进价为每件 元，当售价为每件 元时，每个月可售出 件．根据市场行情， 现决定涨价销售，调查表明，每件商品的售价每上涨 元，每个月会少售出 件，设每件商品的 售价为 元，每个月的销量为 件． 求 与 之间的函数关系式． 当每件商品的售价定为多少元时，每个月的利润恰好为 元．﹐ 当每件商品的售价定为多少元时，每个月获得利润最大？最大月利润为多少？ 24. 图 1 2 （ 1 ） （ 2 ） 已知，在 中， ， 是 边上一点，连接 ，分别以 和 为直 角边作 和 ，使 ，点 ， 在 下方，连接 ． 如图 ，当 ， ， 时，求证： ． ． 如图 ，当 ， ， 时，猜想 和 之间的数量关 系？并说明理由． 图 25. 如图 ，在平面直角坐标系中，一次函数 的图象与 轴交于点 ，与 轴交于 点，抛物线 经 ， 两点，在第一象限的抛物线上取一点 ，过点 作 轴于点 ，交直线 于点 ． / （ 1 ） （ 2 ） （ 3 ） 图 求抛物线的函数表达式． 是否存在点 ，使得 和 相似？若存在，请求出点 的坐标，若不存在， 请说明理由． 如图 ， 是第一象限内抛物线上的动点（不与点 重合），点 是线段 上的动点连 接 ， ，当四边形 是平行四边形且周长最大时，请直接写出点 的坐标． 图