2017-2018学年湖北省孝感市云梦县九年级上期中考试数学试题含答案 10页

‎2017-2018学年湖北省孝感市云梦县九年级（上）期中数学试卷 ‎　‎ 一、选择题（每小题3分，共30分）‎ ‎1．下列图形是我国国产品牌汽车的标识，在这些汽车标识中，是中心对称图形的是（　　）‎ ‎2．若抛物线y=（x﹣m）2+（m﹣1）的顶点在第一象限，则m的取值范围为（　　）‎ A．m＞0 B．m＞1 C．m＞﹣1 D．0＜m＜1[来源:学_科_网Z_X_X_K]‎ ‎3．在某次同学聚会上，每两个人都握一次手，所有人共握手45次，设有x人参加这次聚会，则列出方程正确的是（　　）‎ A．x（x+1）=45 B．x（x﹣1）=45 C．=45 D．=45‎ ‎4．已知x=2是一元二次方程（m﹣2）x2+4x﹣m2=0的一个根，则m的值为（　　）[来源:学,科,网]‎ A．2 B．0或2 C．0或4 D．0‎ ‎5．已知点A（a，1）与点A′（4，b）关于原点对称，则a、b的值分别为（　　）‎ A．a=﹣4，b=﹣1 B．a=﹣1，b=﹣4 C．a=1，b=4 D．a=4，b=1‎ ‎6．我们知道方程x2+2x﹣3=0的解是x1=1，x2=﹣3，现给出另一个方程（2x+3）2+2（2x+3）﹣3=0，它的解是（　　）‎ A．x1=1，x2=3 B．x1=1，x2=﹣3 C．x1=﹣1，x2=3 D．x1=﹣1，x2=﹣3[来源:Zxxk.Com][来源:Z§xx§k.Com]‎ ‎7．若方程ax2+bx+c=0的两个根是﹣4和2，那么二次函数y=ax2+bx+c的图象的对称轴是直线（　　）‎ A．x=﹣2 B．x=﹣1 C．x=0 D．x=1‎ ‎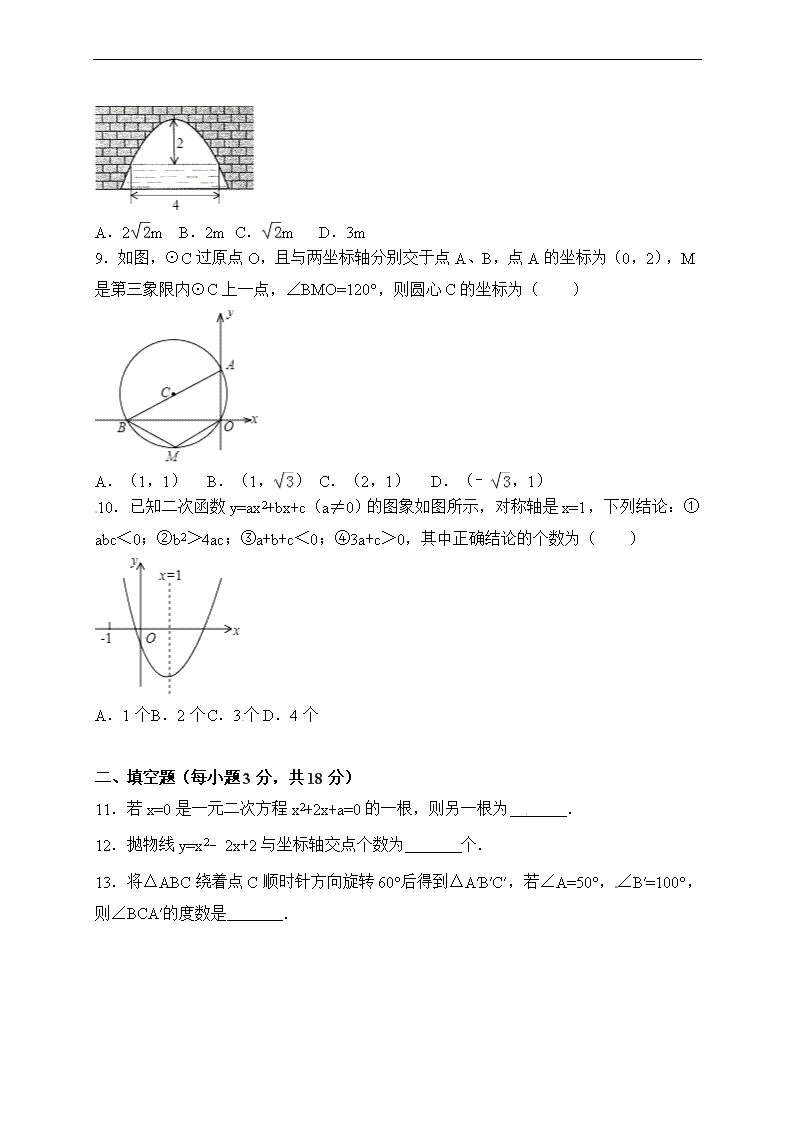8．如图，是一个横断面为抛物线形状的拱桥，当水面宽4m时，拱顶（拱桥洞的最高点）离水面2m，当水面上升1m时，水面的宽为（　　）‎ A．2m B．2m C．m D．3m ‎9．如图，⊙C过原点O，且与两坐标轴分别交于点A、B，点A的坐标为（0，2），M是第三象限内⊙C上一点，∠BMO=120°，则圆心C的坐标为（　　）‎ A．（1，1） B．（1，） C．（2，1） D．（﹣，1）‎ ‎10．已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，对称轴是x=1，下列结论：①abc＜0；②b2＞4ac；③a+b+c＜0；④3a+c＞0，其中正确结论的个数为（　　）‎ ‎[来源:学科网ZXXK]‎ A．1个 B．2个 C．3个 D．4个 ‎　‎ 二、填空题（每小题3分，共18分）‎ ‎11．若x=0是一元二次方程x2+2x+a=0的一根，则另一根为　 　．‎ ‎12．抛物线y=x2﹣2x+2与坐标轴交点个数为　 　个．‎ ‎13．将△ABC绕着点C顺时针方向旋转60°后得到△A′B′C′，若∠A=50°，∠B′=100°，则∠BCA′的度数是　 　．‎ ‎14．若实数x满足x2﹣2x﹣1=0，则2x3﹣7x2+4x﹣2017=　 　．‎ ‎15．如图，MN是半径为1的⊙O的直径，点A在⊙O上，∠AMN=30°，B为AN弧的中点，P是直径MN上一动点，则PA+PB的最小值为　 　．‎ ‎16．如图，点B的坐标是（0，1），AB⊥y轴，垂足为B，点A在直线y=x，将△ABO绕点A顺时针旋转到△AB1O1的位置，使点B的对应点B1落在直线y=x上，再将△AB1O1绕点B1顺时针旋转到△A1B1O2的位置，使点O1的对应点O2落在直线y=x上，依次进行下去…，则点O100的纵坐标是　 　．‎ ‎　‎ 三、解答题（本题8个小题，满分72分）‎ ‎17．（6分）用指定的方法解下列方程：‎ ‎（1）2x2﹣4x+1=0（公式法）‎ ‎（2）2x2+5x﹣3=0（配方法）‎ ‎18．（8分）如图，分别画出△ABC绕点O逆时针旋转90°和180°后的图形．‎ ‎19．（8分）如图，二次函数y=ax2+bx+c（a≠0）的图象的顶点C的坐标为（﹣1，﹣3），与x轴交于A（﹣3，0）、B（1，0），根据图象回答下列问题：‎ ‎（1）写出方程ax2+bx+c=0的根；‎ ‎（2）写出不等式ax2+bx+c＞0的解集；‎ ‎（3）若方程ax2+bx+c=k有实数根，写出实数k的取值范围．‎ ‎20．（8分）已知关于x的一元二次方程x2﹣6x+m+4=0有两个实数根x1，x2．‎ ‎（1）求m的取值范围；‎ ‎（2）若x1，x2满足2x1=|x2|+3，求m的值．‎ ‎21．（10分）如图，AB是⊙O的直径，弦CD⊥AB于点E，点F在⊙O上，FD恰好经过圆心O，连接FB．21教育网 ‎（1）若∠F=∠D，求∠F的度数；‎ ‎（2）若CD=24，BE=8，求⊙O的半径．‎ ‎22．（10分）某城市中心地带有一楼盘，开发商准备以每平方7000元的价格出售，由于国家出台了有关调控房地产的政策，开发商决定下调售价，有两种方案：‎ 方案一：经过连续两次下调售价，以每平方米5670元的价格销售；‎ 方案二：先下调5%，再下调15%；‎ ‎（1）求方案一中平均每次下调的百分率；‎ ‎（2）请问哪种方案对购房者更优惠？为什么？‎ ‎23．（10分）如图，△ABC中，∠ACB=90°，AC=BC=2，将△ABC绕点C逆时针旋转得到△A1B1C，旋转角α（0°＜α＜90°），连接BB1，设CB1交AB于D，AlB1分别交AB，AC于E，F．21cnjy.com ‎（1）求证：△BCD≌△A1CF；‎ ‎（2）若旋转角α为30°，‎ ‎①请你判断△BB1D的形状；‎ ‎②求CD的长．‎ ‎24．（12分）如图，抛物线y=﹣x2+bx+c与x轴交于A、B两点，与y轴交于点C，已知A（﹣1，0），C（0，3）‎ ‎（1）求该抛物线的表达式；‎ ‎（2）求BC的解析式；‎ ‎（3）点M是对称轴右侧点B左侧的抛物线上一个动点，当点M运动到什么位置时，△BCM的面积最大？求△BCM面积的最大值及此时点M的坐标．‎ ‎　‎