- 392.50 KB
- 2021-11-11 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
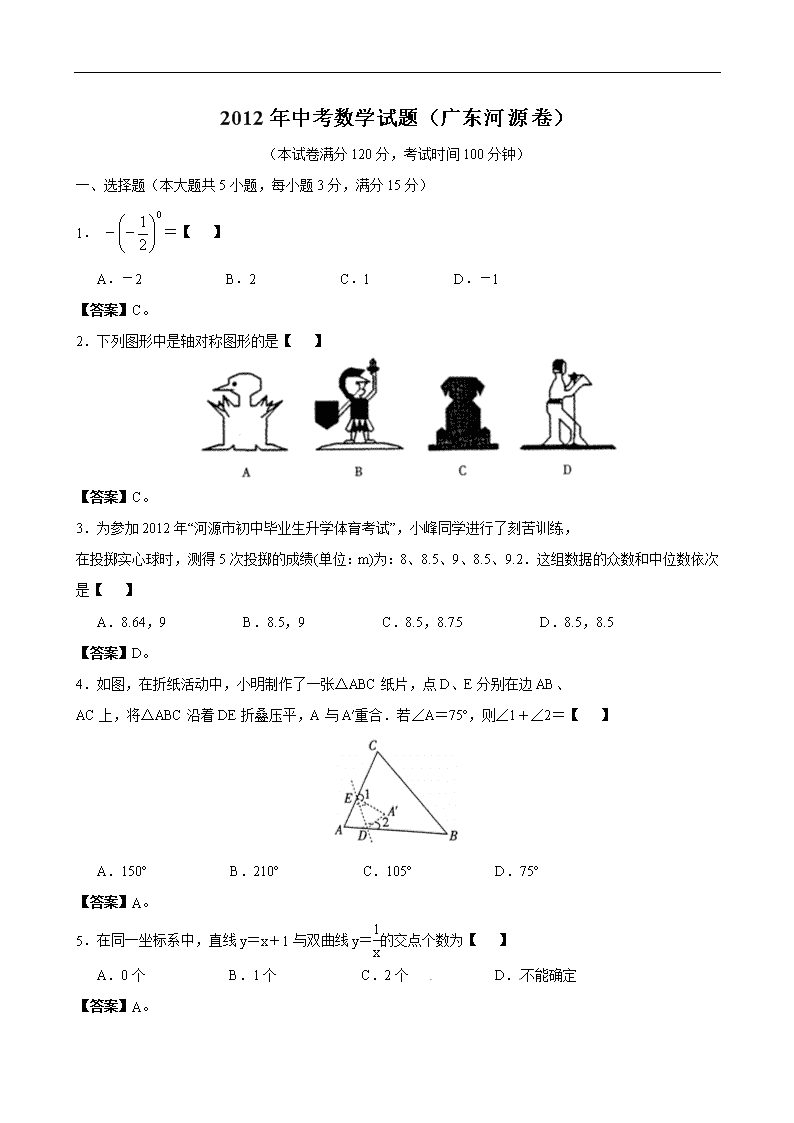
2012 年中考数学试题(广东河源卷)
(本试卷满分 120 分,考试时间 100 分钟)
一、选择题(本大题共 5 小题,每小题 3 分,满分 15 分)
1. =【 】
A.-2 B.2 C.1 D.-1
【答案】C。
2.下列图形中是轴对称图形的是【 】
【答案】C。
3.为参加 2012 年“河源市初中毕业生升学体育考试”,小峰同学进行了刻苦训练,
在投掷实心球时,测得 5 次投掷的成绩(单位:m)为:8、8.5、9、8.5、9.2.这组数据的众数和中位数依次
是【 】
A.8.64,9 B.8.5,9 C.8.5,8.7 5 D.8.5,8.5
【答案】D。
4.如图,在折纸活动中,小明制作了一张△ABC 纸片,点 D、E 分别在边 AB、
AC 上,将△ABC 沿着 DE 折叠压平,A 与 A′重合.若∠A=75º,则∠1+∠2=【 】
A.150º B.210º C.105º D.75º
【答案】A。
5.在同一坐标系中,直线 y=x+1 与双曲线 y=1
x的交点个数为【 】
A.0 个 B.1 个 C.2 个 D. 不能确定
【答案】A。
0
2
1
−−
二、填空题(本大题共 5 小题,每小题 4 分 ,满分 20 分)
6.若代数式-4x6y 与 x2ny 是同类项,则 常数 n 的值为 ▲ .
【答案】3。
7.某市水资源十分丰富,水力资源的理论发电量约为 775 000 千瓦,这个数据用
科学记数法表示为 ▲ 千瓦.
【答案】7.75×105。
8.正六 边形的内角和为 ▲ 度.
【答案】720。
9.春蕾数学兴趣小组用一块正方形木板在阳光下做投 影实验,这块正方形木板在
地面上形成的投影可能是 ▲ (写出符合题意的两个图形即可).
【答案】正方形、菱形(答案不唯一)。
10.如图,连接在一起的两个正方 形的边长都为 1cm,一个微型机器人由点 A 开
始按 ABCDEFCGA…的顺序沿正方形的边 循环移动.①第一次到达点 G 时,微型机器人移动了 ▲
cm;
②当微型机器人移动了 2012cm 时 ,它停在 ▲ 点.
【答案】7;E。
三、解答题(一)(本大题共 5 小题,每小题 6 分,满分 30 分)
11.计算: .
【答案】解:原式= 。
12.解不等式组:{x+3>0,
2(x-1)+3 ≥ 3x.
解不等式组: ,并判断﹣1、 这两个数是否为该不等式组的解.
【答案】解: ,
1
3
160sin2123
−
++−−
33 2 3+2 +3= 3 2 3+ 3+3=32
− ⋅ −
( )
x+3 0
2 x 1 +3 3x
> − ≥
2
( )
x+3 0
2 x 1 +3 3x
> − ≥
①
②
由①得 x>﹣3;由②得 x≤1。
∴原不等式组的解集为:﹣3<x≤1,
13.我市某中学准备在校园内空地上种植桂花树、香樟树、木棉树和柳树,为了解
学生喜爱的树种情况,随机调查了该校部分学生,并将调查结果整理后制成了如下统计图:[来源:学_科_网 Z_X_X_K]
请呢根 据统计图提供的信息,解答以下问题(直接填写答案):
(1)该中学一共随机调查了 人;
(2)条形统计图中的 m= ,m= ;
(3)如果在该校随机调查一位学生,那么该学生喜爱香樟树的概率是 .
【答案】解:(1)200。
(2)70;30。
(3) 。
14.如图,在边长为 1 的小正方形组成的网格中,△AOB 的 三个顶点均在格点上,
点 A、B 的坐标分别为(3,2)、(1,3).△AOB 绕点 O 逆时针旋 转 90º 后得到△A1OB1.
(1)点 A 关于 O 点中心对称的点的坐标为 ;
(2)点 A1 的坐标为 ;
(3)在旋转过程中,点 B 经过的路径为弧 BB1,那么弧 BB1 的长为 .
7
20
【答案】解:(1) (﹣3,﹣2)。
(2) (﹣2,3)。
(3) 。
15.如图,已知 AB=CD,∠B=∠C,AC 和 BD 交于点 O,E 是 AD 的中点,连接 OE.
(1)求证:△AOD≌△DOC;
(2)求∠AEO 的度数.
【答案】解:(1)证明:在△AOB 和△COD 中,∵∠B=∠C,∠AOB=∠DOC,AB=DC,
∴△AOB≌△COD(AAS)。
(2)∵△AOB≌△COD,∴AO=DO。
∵E 是 AD 的中点,∴OE⊥AD。∴∠AEO=90°。
四、解答题(二)(本大题共 4 小题,每小题 7 分,满分 28 分)
16.如图所示的曲线 是函数 y=m-5
x (m 为常数)图象的一支.
(1)求常数 m 的取值范围;
(2)若该函数的图象与正比例函数 y=2x 的图象在第一象限的交点为 A(2,n),求点 A 的坐标及反比例
函数的解析式.
【答案】解:(1)∵函数 y=m-5
x (m 为常数)图象的一支在第一象限,
∴m-5>0,解得 m>5。
(2)∵函数 y=m-5
x 的图象与正比例函数 y=2x 的图象在第一象限的交点为 A(2,n),
∴ ,解得 。
10
2
π
m 5n= 2
n=4
−
n=4
m=13
∴ 点 A 的坐标为(2,4);反比例函数的解析式为 y= 。
17.解方程: 4
x2-1+x+2
1-x=-1.
【答案】解:方程两边都乘以(x+1)(x﹣1),得 4﹣(x+1)(x+2)=﹣(x2﹣1),
整理,得,3x=1,解得 。[来源:Z,xx,k.Com]
经检验, 是原方程的根。
∴原方程的解是 。
18.如图,AC 是⊙O 的直径,弦 BD 交 AC 于点 E.
(1)求证:△ADE∽△BCE;
(2)若 AD2=AC·AE,求证:BC=CD.
【答案】证明:(1)∵∠A 与∠B 都是弧 所对的圆周角, ∴∠A=∠B,
又∵∠AED =∠BEC,∴△ADE∽△BCE。
(2)∵AD2=AE•AC,∴ 。
又∵∠A=∠A,∴△ADE∽△ACD。∴∠AED=∠ADC。
又∵AC 是⊙O 的直径,∴ ∠ADC=90°。∴∠AED=90°。
∴直径 AC⊥BD,∴CD=CB。
8
x
1x= 3
1x= 3
1x= 3
CD
AE AD=AD AC
19.一辆警车在高速公路的 A 处加满油,以每小时 60 千米的速度匀速行驶.已知警车一次加满油后,油
箱内的余油量 y( 升)与行驶的时间 x(小时)的函数关系的图象是如图所示的直线 l 的一部分.
(1)求直线 l 的 函数表达式;[来源:学_科_网]
(2)如果警车要回到 A 处,且要求警车的余油量不能少于 1 0 升,那么警车可以以行驶到离 A 处的最远
距离是多少?
【答案 】解:(1)设直线 l 的解析式是 y=kx+b,由图示,直线经过(1,45),(3,42)两点,得
,解得 。
∴直线 l 的解析式是:y=﹣6x+60。
(2)由题意得:y=﹣6x+60≥10,解得 x≤ 。
∴警车最远的距离可以到: 千米。
五、解答题(三)(本大题共 3 小题,每小题 9 分,满分 27 分)
20.如图,已知△ABC,按如下步骤作图:①分别以 A、C 为圆心,以大于 1
2AC 的长为半径在 AC 的两边
作弧,交于点 M、N;②连接 MN,分别交 AB、AC 于点 D、O;③过点 C 作 CE∥AB 交 MN 于点
E,连接 AE、CD.
(1)求证:四边形 ADEC 是菱形;
(2)当∠ACB=90º,BC=6,△ACD 的周长为 18 时,求四边形 ADEC 的面积.
k+b=45
3k+b=42
k= 6
b=60
−
25
3
25 160 =2503 2
× ×
【答案】(1)证明:由作法可知:直线 DE 是线段 AC 的垂直平分线,
∴AC⊥DE,即∠AOD=∠COE=90°,且 AD=CD,AO=CO。
又∵CE∥AB,∴∠ADO =∠CEO。[来源:学科网 ZXXK]
∴△AOD≌△COE(AAS)。∴OD=OE。∴四边形 ADCE 是菱形。
(2)解:当∠ACB=90°时,
由(1)知 AC⊥DE,∴OD∥BC。
∴△ADO∽△ABC。∴ 。
又∵BC=6,∴OD=3。
又∵△ ADC 的周长为 18,∴AD+AO=9, 即 AD=9﹣AO。
∴ ,解得 AO=4
∴ 。
21.(1)已知方程 x2+px+q =0(p2-4q≥0)的两根为 x1、x2,求证:x1+x2=-p,x1·x2=q.
(2)已知抛物线 y=x2+px+q 与 x 轴交于点 A、B,且过点(―1,―1),设线段 AB 的长为 d,当 p 为
何值时,d2 取得最小值并求出该最小值.
【答案】(1)证明:∵a=1,b=p,c=q,p2﹣4q≥0,
∴ 。
(2)解:把(﹣1,﹣1)代入 y=x2+px+q 得 p﹣q=2,即 q=p﹣2。
设抛物线 y=x2+px+q 与 x 轴交于 A、B 的坐标分别为(x1,0)、(x2,0)。
∵d=|x1﹣x2|,
∴d2=(x1﹣x2)2=(x1+x2)2﹣4 x1•x2=p2﹣4q=p2﹣4p+8=(p﹣2)2+4。
∴当 p=2 时,d 2 的最小值是 4。
OD AO 1
CB AC 2
= =
( )22 2 2OD= AD AO 9 AO AO 3− = − − =
ADCE ADO
1 1S 4S 4 OD AO=4 3 4 242 2∆= = ⋅ ⋅ ⋅ × × × =
1 2 1 2
b cx x = p x x =qa a
+ = − − ⋅ =,
22.如图,矩形 OABC 中,A(6,0)、C(0,2 3)、 D(0,3 3),射线 l 过点 D 且与 x 轴平行, 点 P、Q 分
别是 l 和 x 轴的正半轴上的动点,满足∠PQO=60º.
(1)点 B 的坐标是 ,∠CAO= º,当点 Q 与点 A 重合时,点 P 的坐标为 ;
(2)设点 P 的横坐标为 x,△OPQ 与矩形 OABC 重叠部分的面积为 S,试求 S 与 x 的函数关系式和相应
的自 变量 x 的取值范围.
【答案】解:(1)(6,2 )。 30。(3,3 )。
(2)当 0≤x≤3 时,
如图 1,OI=x,IQ=PI•tan60°=3,OQ=OI+IQ=3+x;
由题意可知直线 l∥BC∥OA,
可得 ,∴EF= (3+x),
此时重叠部分是梯形,其面积为:
当 3<x≤5 时,如图 2,
当 5<x≤9 时,如图 3,
3 3
EF PE DC 3 1= =OQ PO DO 33 3
= = 1
3
EFQO
1 4 3 4 3S S EF OQ OC 3 x x 4 32 3 3
= = + ⋅ = + +梯形 ( ) ( )=
( )
HAQEFQO EFQO
2 2
1S S S S AH AQ2
4 3 3 3 13 3 3x 4 3 x 3 x x3 2 2 3 2
∆= − = − ⋅ ⋅
= + − − − + − =
梯形 梯形
。
1 2S BE OA OC 3 12 x2 3
2 3= x 12 33
= + ⋅ = −
− +
( ) ( )
。
当 x>9 时,如图 4,
。[来源:学科网]
综上所述,S 与 x 的函数关系式为:
。
1 1 18 3 54 3S OA AH 6 =2 2 x x
= ⋅ = ⋅ ⋅
( )
( )
( )
( )
2
4 3 x 4 3 0 x 33
3 13 3 3x x 3 x 52 3 2S
2 3 x 12 3 5 x 93
54 3 x 9x
<
<
>
+ ≤ ≤
− + − ≤=
− + ≤
相关文档
- 2019年山东省滨州市中考数学试题(A2021-11-1125页
- 2014年湖南省长沙市中考数学试题(含2021-11-117页
- 2019山东省青岛市中考数学试题(解析2021-11-1131页
- 2018中考数学试题分类:考点15 反2021-11-1114页
- 2012年江苏省南通市中考数学试题(含2021-11-1114页
- 2013年绍兴市中考数学试题及答案(2021-11-1110页
- 2016年全国各地中考数学试题分类解2021-11-1118页
- 2018年江苏省无锡市中考数学试题含2021-11-1112页
- 2019四川省广安市中考数学试题(解析2021-11-1125页
- 2019广东省深圳中考数学试题(word版2021-11-1112页