- 1.17 MB
- 2021-11-11 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
第
13
课时
二次函数的图象与性质
第三单元 函数及其图象
考点一 二次函数的概念
考点聚焦
一般地
,
形如
①
(
a
,
b
,
c
是常数
,
a
≠0)
的函数
,
叫做二次函数
.
y=ax
2
+
bx
+
c
【
温馨提示
】
函数
y=ax
2
+
bx
+
c
未必是二次函数
,
当
②
时
,
y=ax
2
+
bx
+
c
是二次函数
.
a
≠0
函数
y=ax
2
+
bx
+
c
(
a
,
b
,
c
为常数
,
a
≠0)
a>
0
a<
0
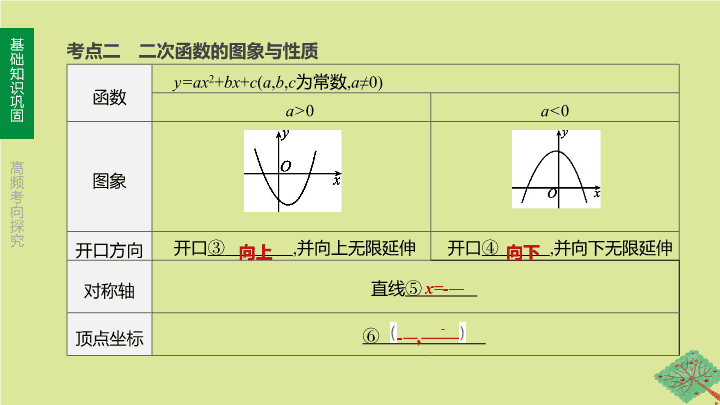
图象
开口方向
开口
③
,
并向上无限延伸
开口
④
,
并向下无限延伸
对称轴
直线
⑤
顶点坐标
⑥
考点二 二次函数的图象与性质
向上
向下
(续表)
减小
增大
增大
减小
(续表)
小
大
考点三 二次函数
y
=
ax
2
+
bx
+
c
(
a
,
b
,
c
为常数
,
a
≠0)
的图象与系数的关系
上
下
y
左
右
(
续表
)
(0,0)
正半轴
负半轴
两
(
续表
)
a
-
b
+
c
-1
考点四 二次函数图象的画法
考点五 二次函数的表示及解析式的求法
1
.
二次函数的三种表示方法
(1)
一般式
:
㉔
.
(2)
顶点式
:
y=a
(
x
-
h
)
2
+
k
(
a
≠0),
其中二次函数图象的顶点坐标是
㉕
.
(3)
两点式
:
y=a
(
x
-
x
1
)(
x
-
x
2
)(
a
≠0),
其图象与
x
轴的交点的坐标为
㉖
.
y=ax
2
+
bx
+
c
(
a
≠0)
(
h
,
k
)
(
x
1
,0),(
x
2
,0)
2
.
二次函数解析式的确定
用待定系数法求二次函数的解析式时
,
注意解析式的设法
,
常见情况如下
:
条件
设法
顶点在原点
y=ax
2
(
a
≠0)
顶点在
y
轴上
y=ax
2
+
c
(
a
≠0,
y
轴为对称轴
)
顶点在
x
轴上
y=a
(
x
-
h
)
2
(
a
≠0,
直线
x=h
是对称轴
)
抛物线过原点
y=ax
2
+
bx
(
a
≠0)
顶点
(
h
,
k
)
y=a
(
x
-
h
)
2
+
k
(
a
≠0)
抛物线与
x
轴的
交点
为
(
x
1
,0),(
x
2
,0)
y=a
(
x
-
x
1
)(
x
-
x
2
)(
a
≠0)
考点六 二次函数图象的平移
抛物线
y=ax
2
+
bx
+
c
(
a
≠0)
可用配方法化成
y=a
(
x
-
h
)
2
+
k
(
a
≠0)
的形式
,
任意抛物线
y=a
(
x
-
h
)
2
+
k
(
a
≠0)
均可由抛物线
y=ax
2
(
a
≠0)
平移得到
,
具体平移方法如图
13-1
所示
(
假设
h
,
k
均为正数
):
图
13-1
【
温馨提示
】
平移规则为
“
上加下减
,
左加右减
”
.
题组一 必会题
对点演练
1
.
[2018·
岳阳
]
抛物线
y=
3(
x
-2)
2
+5
的顶点坐标是
(
)
A
.
(-2,5) B
.
(-2,-5)
C
.
(2,5) D
.
(2,-5)
C
2
.
[2019·
重庆
B
卷
]
抛物线
y=
-3
x
2
+6
x
+2
的对称轴是
(
)
A
.
直线
x=
2 B
.
直线
x=
-2
C
.
直线
x=
1 D
.
直线
x=
-1
C
3
.
一条抛物线和抛物线
y=
-2
x
2
的形状、开口方向完全相同
,
顶点坐标是
(-1,3),
则该抛物线的解析式为
(
)
A
.y=
-2(
x
-1)
2
+3
B
.y=
-2(
x
+1)
2
+3
C
.y=
-(2
x
+1)
2
+3
D
.y=
-(2
x
-1)
2
+3
B
4
.
[2019·
雅安
]
在平面直角坐标系中
,
对于二次函数
y=
(
x
-2)
2
+1,
下列说法中错误的是
(
)
A
.y
的最小值为
1
B
.
图象顶点坐标为
(2,1),
对称轴为直线
x=
2
C
.
当
x<
2
时
,
y
的值随
x
值的增大而增大
,
当
x
≥2
时
,
y
的值随
x
值的增大而减小
D
.
它的图象可以由
y=x
2
的图象向右平移
2
个单位长度
,
再向上平移
1
个单位长度得到
C
5
.
[2019·
河南
]
已知抛物线
y=
-
x
2
+
bx
+4
经过
(-2,
n
)
和
(4,
n
)
两点
,
则
n
的值为
(
)
A
.
-2 B
.
-4
C
.
2 D
.
4
[
答案
]B
6
.
[2019·
攀枝花
]
在同一坐标系中
,
二次函数
y=ax
2
+
bx
与一次函数
y=bx
-
a
的图象可能是
(
)
C
图
13-2
题组二 易错题
【
失分点
】
考虑二次函数的增减性时
,
要关注自变量的取值及对称轴的位置
,
因为二次函数的增减性是分区域的
.
7
.
[2019·
温州
]
已知二次函数
y=x
2
-4
x
+2,
关于该函数在
-1≤
x
≤3
的取值范围内
,
下列说法正确的是
(
)
A
.
有最大值
-1,
有最小值
-2
B
.
有最大值
0,
有最小值
-1
C
.
有最大值
7,
有最小值
-1
D
.
有最大值
7,
有最小值
-2
[
答案
]D
[
解析
]
∵二次函数
y=x
2
-4
x
+2
=
(
x
-2)
2
-2,
∴该函数在
-1≤
x
≤3
的取值范围内
,
当
x=
2
时
,
y
有最小值
-2;
当
x=
-1
时
,
y
有最大值
7
.
故选
D
.
8
.
[2018·
潍坊
]
已知二次函数
y=
-(
x
-
h
)
2
(
h
为常数
),
当自变量
x
的值满足
2≤
x
≤5
时
,
与其对应的函数值
y
的最大值为
-1,
则
h
的值为
(
)
A
.
3
或
6 B
.
1
或
6
C
.
1
或
3 D
.
4
或
6
[
答案
]B
[
解析
]
二次函数
y=
-(
x
-
h
)
2
,
当
x=h
时
,
有最大值
0,
而当自变量
x
的值满足
2≤
x
≤5
时
,
与其对应的函数值
y
的最大值为
-1,
故
h<
2
或
h>
5
.
当
h<
2
时
,2≤
x
≤5
时
,
y
随
x
的增大而减小
,
故当
x=
2
时
,
y
有最大值
,
此时
-(2-
h
)
2
=
-1,
解得
:
h
1
=
1,
h
2
=
3(
舍去
),
此时
h=
1;
当
h>
5
时
,2≤
x
≤5
时
,
y
随
x
的增大而增大
,
故当
x=
5
时
,
y
有最大值
,
此时
-(5-
h
)
2
=
-1,
解得
:
h
1
=
6,
h
2
=
4(
舍去
),
此时
h=
6
.
综上可知
,
h=
1
或
6,
故选
B
.
9
.
一元二次方程
x
2
+(
m
-5)
x
+1-
m=
0
的一根大于
3,
另一根小于
3,
则
m
的取值范围
为
.
考向一 二次函数的图象与性质
图
13-3
解
:(1)
y=x
2
-2
x
-8
=
(
x
-1)
2
-9,
开口向上
,
对称轴为直线
x=
1,
顶点为
D
(1,-9)
.
例
1
对于抛物线
y=x
2
-2
x
-8
.
(2)
求出它与
y
轴的交点
C
的坐标
;
图
13-3
(2)
令
x=
0,
则
y=
-8,
∴
C
(0,-8)
.
例
1
对于抛物线
y=x
2
-2
x
-8
.
(3)
求出它与
x
轴的交点
A
,
B
的坐标
(
A
在
B
左侧
);
图
13-3
(3)
令
y=
0,
则
x
2
-2
x
-8
=
0,
∴
x
1
=
-2,
x
2
=
4,
∴
A
(-2,0),
B
(4,0)
.
例
1
对于抛物线
y=x
2
-2
x
-8
.
(4)
画出它的图象
;
图
13-3
(4)
如图
:
例
1
对于抛物线
y=x
2
-2
x
-8
.
(5)
当
x
为何值时
,
y
随
x
的增大而增大
;
图
13-3
(5)
当
x
≥1
时
,
y
随
x
的增大而增大
.
例
1
对于抛物线
y=x
2
-2
x
-8
.
(6)
求
CB
和
AD
的长
;
图
13-3
例
1
对于抛物线
y=x
2
-2
x
-8
.
(7)
求
△
CDB
的面积
.
图
13-3
|
考向精练
|
1
.
[2019·
呼和浩特
3
题
]
二次函数
y=ax
2
与一次函数
y=ax
+
a
在同一坐标系中的大致图象可能是
(
)
D
图
13-4
2
.
[2013·
呼和浩特
8
题
]
在同一平面直角坐标系中
,
函数
y=mx
+
m
和
y=
-
mx
2
+2
x
+2(
m
是常数
,
m
≠0)
的图象可能是
(
)
图
13-5
D
3
.
[2019·
烟台
]
已知二次函数
y=ax
2
+
bx
+
c
的
y
与
x
的部分对应值如下表
:
下列结论
:
①抛物线的开口向上
;
②抛物线的对称轴为直线
x=
2;
③当
0
0;
④抛物线与
x
轴的两个交点间的距离是
4;
⑤若
A
(
x
1
,2),
B
(
x
2
,3)
是抛物线上两点
,
则
x
1
x
2
,
所以结论⑤错误
.
4
.
当
a
≤
x
≤
a
+1
时
,
函数
y=x
2
-2
x
+1
的最小值为
1,
则
a
的值为
(
)
A
.
-1 B
.
2
C
.
0
或
2 D
.
-1
或
2
[
答案
] D
[
解析
]
y=x
2
-2
x
+1
=
(
x
-1)
2
,
该函数在实数范围内最小值为
0,
但题中说当
a
≤
x
≤
a
+1
时
,
函数
y=x
2
-2
x
+1
的最小值为
1,
因此
,
当
x=a
或
x=a
+1
时
,
函数值为
1,
令
y=
1,
可得
x
1
=
0,
x
2
=
2,
再由该函数的增减性可知
a
+1
=
0,
或
a=
2,
即
a=
-1
或
2,
故选
D
.
5
.
已知二次函数
y=
-(
x
-1)
2
+2,
当
t
1
时
,
y
随
x
的增大而减小
,
而
t
0;
③
a
-
b
+
c<
0;
④
m>
-2
.
其中正确结论的个数是
(
)
A
.
1 B
.
2 C
.
3 D
.
4
图
13-6
[
答案
] B
[
解析
]
直接利用抛物线与
x
轴交点个数以及抛物线与方程之间的关系、函数图象与各系数之间的关系分析
.
图象与
x
轴有两个交点
,
则
b
2
-4
ac>
0,
故①错误
;
∵图象开口向上
,
∴
a>
0,
∵对称轴在
y
轴右侧
,
∴
a
,
b
异号
,
∴
b<
0,
∵图象与
y
轴交于负半轴
,
∴
c<
0,
∴
abc>
0,
故②正确
;
当
x=
-1
时
,
a
-
b
+
c>
0,
故③错误
;
抛物线
y=ax
2
+
bx
+
c
顶点坐标的纵坐标为
-2,
∵关于
x
的一元二次方程
ax
2
+
bx
+
c
-
m=
0
有两个不相等的实数根
,
∴
m>
-2,
故④正确
.
故选
B
.
【
方法点析
】
解此类问题的一般步骤
:
①根据抛物线的开口方向判定
a
的符号
:
开口向上
,
则
a>
0;
开口向下
,
则
a<
0
.
②根据对称轴的位置和
a
的符号判定
b
的符号
:
对称轴在
y
轴左侧
,
则
a
,
b
同号
;
对称轴在
y
轴右侧
,
则
a
,
b
异号
.
③由抛物线与
y
轴的交点判断
c
的符号
:
交点在
y
轴正半轴
,
则
c>
0;
交点在
y
轴负半轴
,
则
c<
0
.
④根据
a
,
b
,
c
的符号判定
ab
,
bc
,
ac
,
abc
的符号
.
⑤根据抛物线与
x
轴的交点个数判定
b
2
-4
ac
与
0
的大小关系
.
⑥特殊等式的判断
:
见到
a
+
b
+
c
(
或
4
a
+2
b
+
c
),
则令
x=
1(
或
x=
2),
看抛物线上对应点的纵坐标位置
;
见到
a
-
b
+
c
(
或
4
a
-2
b
+
c
),
则令
x=
-1(
或
x=
-2),
看抛物线上对应点的纵坐标的位置
,
根据位置判定其符号
.
|
考向精练
|
1
.
[2019·
玉泉区模拟
]
已知二次函数
y=ax
2
+
bx
+
c
(
a
≠0)
的图象如图
13-7
所示
,
有下列
4
个结论
:
①
a<
0;
②
b>
0;
③
b
4
ac
;
③
a
+
b
+2
c<
0;
④
3
a
+
c>
0
.
其中正确的是
(
)
A
.
①④
B
.
②④
C
.
①②③
D
.
①②③④
图
13-8
[
答案
] D
3
.
[2019·
赤峰
]
二次函数
y=ax
2
+
bx
+
c
(
a
≠0)
的图象如图
13-9
所示
,
下列结论
:
①
b>
0;
②
a
-
b
+
c=
0;
③一元二次方程
ax
2
+
bx
+
c
+1
=
0(
a
≠0)
有两个不相等的实数根
;
④当
x<
-1
或
x>
3
时
,
y>
0
.
上述结论中正确的是
.
(
填上所有正确结论的序号
)
图
13-9
[
答案
]
②③④
[
解析
]
由图可知
,
对称轴为直线
x=
1,
与
x
轴的一个交点为
(3,0),
∴
b=
-2
a
,
与
x
轴另一个交点的坐标为
(-1,0),
①∵
a>
0,
∴
b<
0,
∴①错误
;
②当
x=
-1
时
,
y=
0,
∴
a
-
b
+
c=
0,
②正确
;
③一元二次方程
ax
2
+
bx
+
c
+1
=
0
的根可以看作抛物线
y=ax
2
+
bx
+
c
与直线
y=
-1
的交点的横坐标
,
由图象可知抛物线
y=ax
2
+
bx
+
c
与直线
y=
-1
有两个不同的交点
,
∴一元二次方程
ax
2
+
bx
+
c
+1
=
0(
a
≠0)
有两个不相等的实数根
,
∴③正确
;
④由图象可知
,
当
y>
0
时
,
x<
-1
或
x>
3,
∴④正确
.
故答案为②③④
.
考向三 二次函数图象的平移与旋转
例
3
[2019·
绍兴
]
在平面直角坐标系中
,
抛物线
y=
(
x
+5)(
x
-3)
经过变换后得到抛物线
y=
(
x
+3)(
x
-5),
则这个变换可以是
(
)
A
.
向左平移
2
个单位
B
.
向右平移
2
个单位
C
.
向左平移
8
个单位
D
.
向右平移
8
个单位
[
答案
]
B
[
解析
]
y=
(
x
+5)(
x
-3)
=
(
x
+1)
2
-16,
顶点坐标是
(-1,-16)
.
y=
(
x
+3)(
x
-5)
=
(
x
-1)
2
-16,
顶点坐标是
(1,-16)
.
所以将抛物线
y=
(
x
+5)(
x
-3)
向右平移
2
个单位长度得到抛物线
y=
(
x
+3)(
x
-5),
故选
B
.
|
考向精练
|
1
.
将二次函数
y=x
2
-2
x
+1
的图象绕它的顶点
A
旋转
180°,
则旋转后的抛物线所对应的函数解析式为
(
)
A
.y=
-
x
2
+2
x
+1 B
.y=
-
x
2
-2
x
+1
C
.y=
-
x
2
+2
x
-1 D
.y=x
2
+2
x
+1
C
2
.
在平面直角坐标系中
,
如果抛物线
y=
3
x
2
不动
,
而把
x
轴
,
y
轴分别向上
,
向右平移
3
个单位
,
那么在新坐标系中抛物线的解析式为
.
y=
3(
x
+3)
2
-3
3
.
已知抛物线
y=a
(
x
-
h
)
2
的对称轴为直线
x=
-2,
且过点
(1,-3)
.
(1)
求抛物线的解析式
;
(2)
求将
(1)
中抛物线向右平移
3
个单位得到的抛物线的解析式
;
(3)
若
(2)
中抛物线的顶点不动
,
将抛物线沿
x
轴翻折
,
写出翻折后抛物线的解析式
.
考向四 二次函数解析式的确定
例
4
根据条件求解析式
.
(1)
已知二次函数图象经过点
(2,-5),(-1,4),(-2,3),
求解析式
;
(2)
已知二次函数图象经过点
(-2,3),
且顶点为
(-1,4),
求解析式
;
(3)
已知二次函数图象经过点
(-3,0),(1,0),(0,3),
求解析式
;
(4)
已知二次函数图象经过点
(-2,3),(-1,4),(0,3),
求解析式
;
(5)
已知二次函数图象经过点
(-3,0),(-1,4),(1,0),
求解析式
.
例
4
根据条件求解析式
.
(2)
已知二次函数图象经过点
(-2,3),
且顶点为
(-1,4),
求解析式
;
(2)
∵顶点为
(-1,4),
∴设解析式为
y=a
(
x
+1)
2
+4
.
将
(-2,3)
代入得
a=
-1,
∴
y=
-(
x
+1)
2
+4
.
例
4
根据条件求解析式
.
(3)
已知二次函数图象经过点
(-3,0),(1,0),(0,3),
求解析式
;
(3)
∵二次函数图象与
x
轴交于
(-3,0),(1,0)
两点
,
∴设解析式为
y=a
(
x
+3)(
x
-1),
将
(0,3)
代入得
a=
-1,
∴
y=
-(
x
+3)(
x
-1),
即
y=
-
x
2
-2
x
+3
.
例
4
根据条件求解析式
.
(4)
已知二次函数图象经过点
(-2,3),(-1,4),(0,3),
求解析式
;
(4)
设对称点式为
y=a
(
x
+2)(
x
-0)+3,
将
(-1,4)
代入得
a=
-1,
∴
y=
-(
x
+2)
x
+3,
即
y=
-
x
2
-2
x
+3
.
例
4
根据条件求解析式
.
(5)
已知二次函数图象经过点
(-3,0),(-1,4),(1,0),
求解析式
.
(5)
设交点式为
y=a
(
x
+3)(
x
-1),
将
(-1,4)
代入得
a=
-1,
∴
y=
-
x
2
-2
x
+3
.
|
考向精练
|
2
.
[2019·
泰州
]
如图
13-10,
在平面直角坐标系
xOy
中
,
二次函数图象的顶点坐标为
(4,-3),
该图象与
x
轴相交于点
A
,
B
,
与
y
轴相交于点
C
,
其中点
A
的横坐标为
1
.
(1)
求该二次函数的表达式
;
(2)
求
tan
∠
ABC.
图
13-10
2
.
[2019·
泰州
]
如图
13-10,
在平面直角坐标系
xOy
中
,
二次函数图象的顶点坐标为
(4,-3),
该图象与
x
轴相交于点
A
,
B
,
与
y
轴相交于点
C
,
其中点
A
的横坐标为
1
.
(2)
求
tan
∠
ABC.
图
13-10