中考数学专题复习练习：二次函数与圆 5页

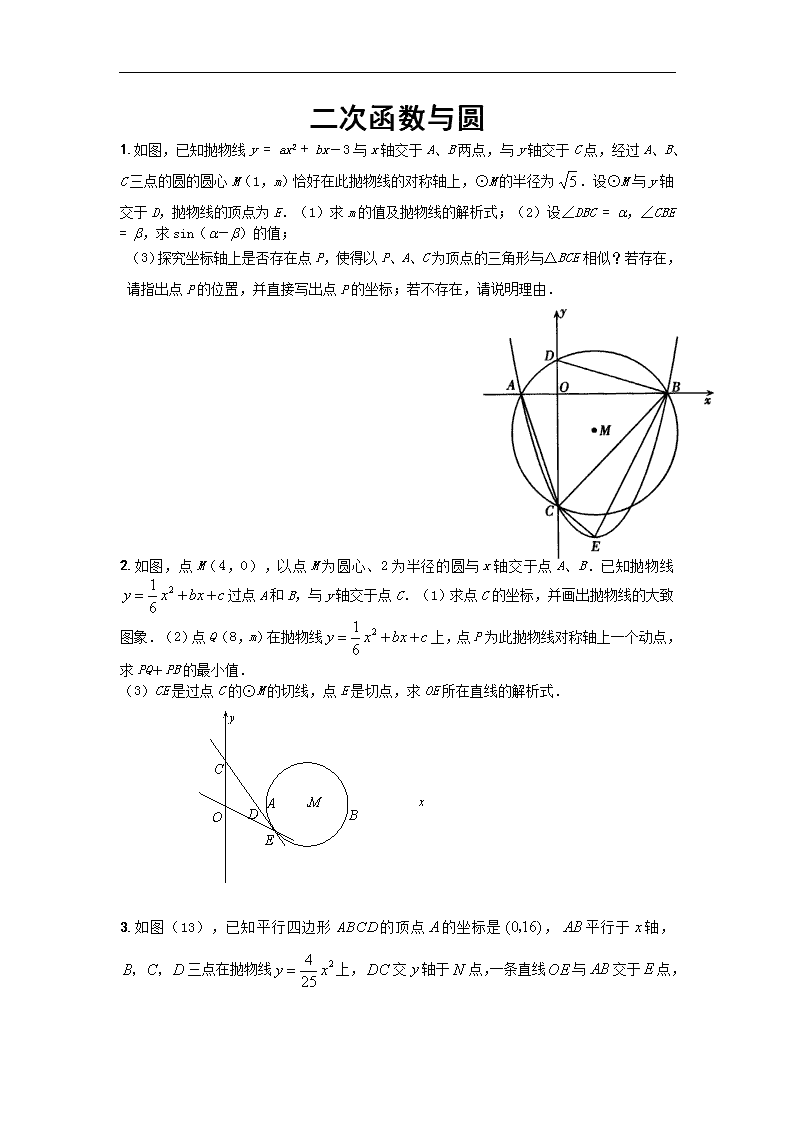
二次函数与圆 ‎1.如图，已知抛物线y = ax2 + bx－3与x轴交于A、B两点，与y轴交于C点，经过A、B、C三点的圆的圆心M（1，m）恰好在此抛物线的对称轴上，⊙M的半径为．设⊙M与y轴交于D，抛物线的顶点为E．（1）求m的值及抛物线的解析式；（2）设∠DBC = a，∠CBE = b，求sin（a－b）的值；‎ ‎（3）探究坐标轴上是否存在点P，使得以P、A、C为顶点的三角形与△BCE相似？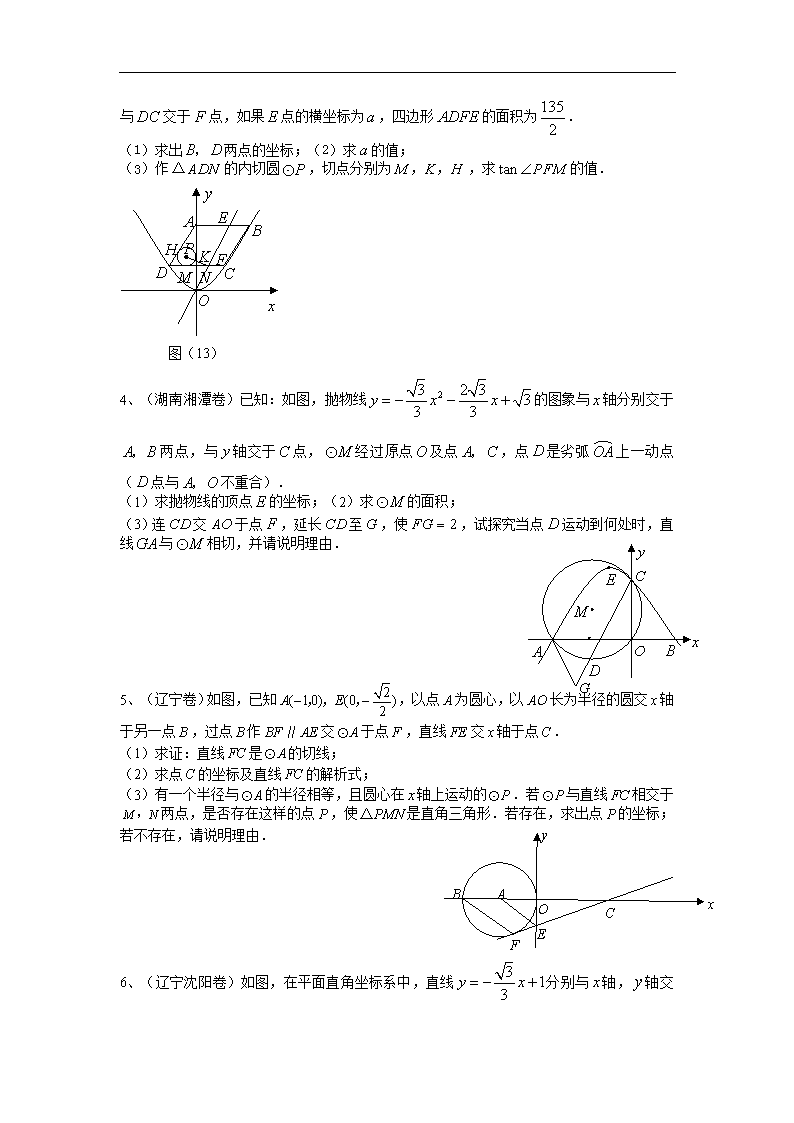若存在，请指出点P的位置，并直接写出点P的坐标；若不存在，请说明理由．‎ ‎2.如图，点M（4，0），以点M为圆心、2为半径的圆与x轴交于点A、B．已知抛物线过点A和B，与y轴交于点C．（1）求点C的坐标，并画出抛物线的大致图象．（2）点Q（8，m）在抛物线上，点P为此抛物线对称轴上一个动点，求PQ＋PB的最小值． （3）CE是过点C的⊙M的切线，点E是切点，求OE所在直线的解析式． ‎C A M B x y O D E ‎3.如图（13），已知平行四边形的顶点的坐标是，平行于轴，三点在抛物线上，交轴于点，一条直线与交于 点，与交于点，如果点的横坐标为，四边形的面积为．‎ ‎（1）求出两点的坐标；（2）求的值；‎ ‎（3）作的内切圆，切点分别为，求的值．‎ 图（13）‎ ‎4、（湖南湘潭卷）已知：如图，抛物线的图象与轴分别交于两点，与轴交于点，经过原点及点，点是劣弧上一动点（点与不重合）．‎ ‎（1）求抛物线的顶点的坐标；（2）求的面积；‎ ‎（3）连交于点，延长至，使，试探究当点运动到何处时，直线与相切，并请说明理由．‎ ‎5、（辽宁卷）如图，已知，以点为圆心，以长为半径的圆交轴于另一点，过点作交于点，直线交轴于点．‎ ‎（1）求证：直线是的切线；‎ ‎（2）求点的坐标及直线的解析式；‎ x y A B C O F E ‎（3）有一个半径与的半径相等，且圆心在轴上运动的．若与直线相交于两点，是否存在这样的点，使是直角三角形．若存在，求出点的坐标；若不存在，请说明理由．‎ ‎ ‎ ‎6、（辽宁沈阳卷）如图，在平面直角坐标系中，直线分别与轴，轴交于点，点．‎ ‎（1）以为一边在第一象限内作等边及的外接圆（用尺规作图，不要求写作法，但要保留作图痕迹）；‎ ‎（2）若与轴的另一个交点为点，求，，，四点的坐标；‎ ‎（3）求经过，，三点的抛物线的解析式，并判断在抛物线上是否存在点，使的面积等于的面积？若存在，请直接写出所有符合条件的点的坐标；若不存在，请说明理由．‎ ‎．‎ ‎7、（山东滨州卷）已知：抛物线与轴相交于两点，且．（Ⅰ）若，且为正整数，求抛物线的解析式；（Ⅱ）若，求的取值范围；‎ ‎（Ⅲ）试判断是否存在，使经过点和点的圆与轴相切于点，若存在，求出的值；若不存在，试说明理由；‎ ‎（Ⅳ）若直线过点，与（Ⅰ）中的抛物线相交于两点，且使，求直线的解析式．‎ ‎8、（四川课改卷）如图，在平面直角坐标系中，已知点，，以为边在轴下方作正方形，点是线段与正方形的外接圆除点以外的另一个交点，连结与相交于点．‎ ‎（1）求证：；‎ ‎（2）设直线是的边的垂直平分线，且与相交于点．若是的外心，试求经过三点的抛物线的解析表达式；‎ ‎（3）在（2）的条件下，在抛物线上是否存在点，使该点关于直线的对称点在轴上？若存在，求出所有这样的点的坐标；若不存在，请说明理由．‎ A E O D C B G F x y l Q ‎9、（浙江卷）在平面直角坐标系xOy中，已知直线l1经过点A(-2，0)和点B(0，)，直线l2的函数表达式为，l1与l2相交于点P．⊙C是一个动圆，圆心C在直线l1上运动，设圆心C的横坐标是a．过点C作CM⊥x轴，垂足是点M．‎ ‎(1)　填空：直线l1的函数表达式是 ，交点P的坐标是 ，∠FPB的度数是 ；‎ ‎(2)　当⊙C和直线l2相切时，请证明点P到直线CM的距离等于⊙C的半径R，并写出R=时a的值.‎ ‎2‎ ‎1‎ ‎3‎ ‎4‎ ‎1‎ ‎2‎ ‎3‎ ‎-1‎ ‎-2‎ ‎-3‎ ‎-1‎ y x O A B E F P l1‎ l2‎ C ‎(3)　当⊙C和直线l2不相离时，已知⊙C的半径R=，记四边形NMOB的面积为S(其中点N是直线CM与l2的交点)．S是否存在最大值？若存在，求出这个最大值及此时a的值；若不存在，请说明理由．‎ ‎10、（山东济南课改卷）如图1，已知中，，．过点作，且，连接交于点．‎ ‎（1）求的长；‎ ‎（2）以点为圆心，为半径作，试判断与是否相切，并说明理由；‎ A B C P E E A B C P Ｄ 图1‎ 图2‎ ‎（3）如图2，过点作，垂足为．以点为圆心，为半径作；以点为圆心，为半径作．若和的大小是可变化的，并且在变化过程中保持和相切，且使点在的内部，点在的外部，求和的变化范围．‎ ‎11、（江苏宿迁课改卷）设边长为‎2a的正方形的中心A在直线l上，它的一组对边垂直于直线l，半径为r的⊙O的圆心O在直线l上运动，点A、O间距离为d．‎ ‎（1）如图①，当r＜a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：‎ d、a、r之间关系 公共点的个数 d＞a＋r 图①‎ d＝a＋r a－r＜d＜a＋r d＝a－r d＜a－r 所以，当r＜a时，⊙O与正方形的公共点的个数可能有　　　　　　　　　个；‎ ‎（2）如图②，当r＝a时，根据d与a、r之间关系，将⊙O与正方形的公共点个数填入下表：‎ d、a、r之间关系 图②‎ 公共点的个数 d＞a＋r d＝a＋r a≤d＜a＋r d＜a 所以，当r＝a时，⊙O与正方形的公共点个数可能有　　　　　　　　个；‎ 图③‎ ‎（3）如图③，当⊙O与正方形有5个公共点时，试说明r＝a；‎ ‎（4）就r＞a的情形，请你仿照“当……时，⊙O与正方形的公共点个数可能有 ‎　 　 个”的形式，至少给出一个关于“⊙O与正方形的公共点个数”的正确结论．‎ ‎43、（山东枣庄课改卷）半径为2.5的⊙O中，直径AB的不同侧有定点C和动点P．已知BC ：CA＝4 : 3，点P在上运动，过点C作CP的垂线，与PB的延长线交于点O ‎（1）当点P与点C关于AB对称时，求CQ的长；‎ ‎（2）当点P运动到的中点时，求CQ的长； ‎ ‎（3）当点P运动到什么位置时，CQ取到最大值？求此时CQ的长．‎