初中数学中考复习课件章节考点专题突破：考点突破专题7运动型问题 20页

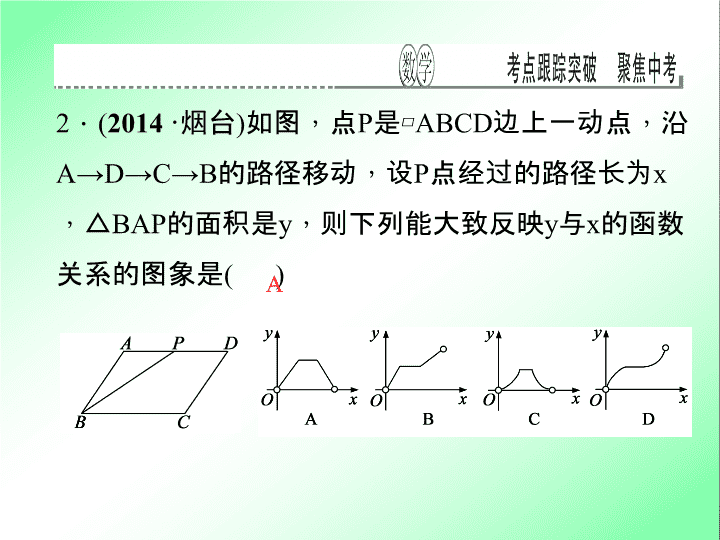
专题跟踪突破七　运动型问题 一、选择题 ( 每小题 10 分 ， 共 40 分 ) 1 ． ( 2013 · 新疆 ) 如图， Rt △ ABC 中 ， ∠ ACB ＝ 90° ， ∠ ABC ＝ 60° ， BC ＝ 2 cm ， 点 D 为 BC 的中点 ， 若动点 E 以 1 cm / s 的速度从 A 点出发 ， 沿着 A → B → A 的方向运动 ， 设 E 点的运动时间为 t 秒 (0 ≤ t ＜ 6) ， 连接 DE ， 当 △ BDE 是直角三角形时 ， t 的值为 ( ) A ． 2 B ． 2.5 或 3.5 C ． 3.5 或 4.5 D ． 2 或 3.5 或 4.5 D 2 ． ( 2014 · 烟台 ) 如图 ， 点 P 是 ▱ ABCD 边上一动点 ， 沿 A → D → C → B 的路径移动 ， 设 P 点经过的路径长为 x ， △ BAP 的面积是 y ， 则下列能大致反映 y 与 x 的函数关系的图象是 ( ) A 3 ． ( 2013 · 盘锦 ) 如图 ， 将边长为 4 的正方形 ABCD 的一边 BC 与直角边分别是 2 和 4 的 Rt △ GEF 的一边 GF 重合．正方形 ABCD 以每秒 1 个单位长度的速度沿 GE 向右匀速运动 ， 当点 A 和点 E 重合时正方形停止运动．设正方形的运动时间为 t 秒 ， 正方形 ABCD 与 Rt △ GEF 重叠部分面积为 S ， 则 S 关于 t 的函数图象为 ( ) B 4 ． ( 2013 · 龙岩 ) 如图 ， 在平面直角坐标系 xOy 中 ， A(0 ， 2) ， B(0 ， 6) ， 动点 C 在直线 y ＝ x 上．若以 A ， B ， C 三点为顶点的三角形是等腰三角形 ， 则点 C 的个数是 ( ) A ． 2 B ． 3 C ． 4 D ． 5 B 二、填空题 ( 每小题 10 分 ， 共 20 分 ) 5 ． ( 2014 · 徐州 ) 如图 ① ， 在正方形 ABCD 中 ， 点 P 沿边 DA 从点 D 开始向点 A 以 1 cm / s 的速度移动；同时 ， 点 Q 沿边 AB ， BC 从点 A 开始向点 C 以 2 cm / s 的速度移动．当点 P 移动到点 A 时 ， P ， Q 同时停止移动．设点 P 出发 x s 时 ， △ PAQ 的面积为 y cm 2 ， y 与 x 的函数图象如图 ② ， 则线段 EF 所在的直线对应的函数关系式为 ． y ＝－ 3x ＋ 18 6 ． ( 2014 · 陕西 ) 如图 ， ⊙ O 的半径是 2 ， 直线 l 与 ⊙ O 相交于 A ， B 两点 ， M ， N 是 ⊙ O 上的两个动点 ， 且在直线 l 的异侧 ， 若 ∠ AMB ＝ 45° ， 则四边形 MANB 面积的最大值是 ____ ． 7 ． (12 分 ) ( 2014 · 武汉 ) 如图 ， Rt △ ABC 中 ， ∠ ACB ＝ 90° ， AC ＝ 6 cm ， BC ＝ 8 cm ， 动点 P 从点 B 出发 ， 在 BA 边上以每秒 5 cm 的速度向点 A 匀速运动 ， 同时动点 Q 从点 C 出发 ， 在 CB 边上以每秒 4 cm 的速度向点 B 匀速运动 ， 运动时间为 t 秒 (0 ＜ t ＜ 2) ， 连接 PQ. (1) 若 △ BPQ 与 △ ABC 相似 ， 求 t 的值； (2) 连接 AQ ， CP ， 若 AQ ⊥ CP ， 求 t 的值； (3) 试证明： PQ 的中点在 △ ABC 的一条中位线上． 8 ． (12 分 ) ( 2014 · 巴中 ) 如图 ， 在平面直角坐标系 xOy 中 ， 抛物线 y ＝ ax 2 ＋ bx － 4 与 x 轴交于点 A( － 2 ， 0) 和点 B ， 与 y 轴交于点 C ， 直线 x ＝ 1 是该抛物线的对称轴． (1) 求抛物线的解析式； ( 2 ) 若两动点 M ， H 分别从点 A ， B 以每秒 1 个单位长度的速度沿 x 轴同时出发相向而行 ， 当点 M 到达原点时 ， 点 H 立刻掉头并以每秒 3 2 个单位长度的速度向点 B 方向移动 ， 当点 M 到达抛物线的对称轴 时 ， 两点停止运动 ， 经过点 M 的直线 l ⊥ x 轴 ， 交 AC 或 BC 于点 P ， 设点 M 的运动时间为 t 秒 ( t ＞ 0 ) ． 求点 M 的运动时间 t 与 △ APH 的 面积 S 的函数关系式 ， 并求出 S 的最大值 ． (2) 分两种情况： ① 当 0 ＜ t ≤ 2 时 ， ∵ PM ∥ OC ， ∴△ AMP ∽△ AOC ， ∴ PM OC ＝ AM AO ， 即 PM 4 ＝ t 2 ， ∴ PM ＝ 2t. 解方程 1 2 x 2 － x － 4 ＝ 0 ， 得 x 1 ＝－ 2 ， x 2 ＝ 4 ， ∵ A ( － 2 ， 0 ) ， ∴ B (4 ， 0 ) ， ∴ AB ＝ 4 － ( － 2) ＝ 6. ∵ AH ＝ AB － BH ＝ 6 － t ， ∴ S ＝ 1 2 PM·AH ＝ 1 2 × 2t (6 － t) ＝－ t 2 ＋ 6t ＝－ (t － 3) 2 ＋ 9 ， 当 t ＝ 2 时 ， S 的最大值为 8 ② 当 2 ＜ t ≤ 3 时 ， 过点 P 作 PM ⊥ x 轴于 M ， 作 PF ⊥ y 轴于点 F ， 则 △ COB ∽△ CFP ， 又 ∵ CO ＝ OB ， ∴ FP ＝ FC ＝ t － 2 ， PM ＝ 4 － (t － 2) ＝ 6 － t ， AH ＝ 4 ＋ 3 2 (t － 2) ＝ 3 2 t ＋ 1 ， ∴ S ＝ 1 2 PM·AH ＝ 1 2 (6 － t )( 3 2 t ＋ 1) ＝－ 3 4 t 2 ＋ 4t ＋ 3 ＝－ 3 4 (t － 8 3 ) 2 ＋ 25 3 ， 当 t ＝ 8 3 时 ， S 最大 值为 25 3 . 综上所述 ， 点 M 的运动时间 t 与 △ APH 面积 S 的函数关系式是 S ＝ î í ì － t 2 ＋ 6t （ 0 ＜ t ≤ 2 ） ， － 3 4 t 2 ＋ 4t ＋ 3 （ 2 ＜ t ≤ 3 ） ， S 的最大值为 25 3 9 ． (16 分 ) ( 2013 · 岳阳 ) 某数学兴趣小组开展了一次课外活动 ， 过程如下：如图 ， 正方形 ABCD 中 ， AB ＝ 6 ， 将三角板放在正方形 ABCD 上 ， 使三角板的直角顶点与 D 点重合．三角板的一边交 AB 于点 P ， 另一边交 BC 的延长线于点 Q. (1) 求证： DP ＝ DQ ； (2) 如图 ② ， 小明在图 ① 的基础上作 ∠ PDQ 的平分线 DE 交 BC 于点 E ， 连接 PE ， 他发现 PE 和 QE 存在一定的数量关系 ， 请猜测他的结论并予以证明； (3) 如图 ③ ， 固定三角板直角顶点在 D 点不动 ， 转动三角板 ， 使三角板的一边交 AB 的延长线于点 P ， 另一边交 BC 的延长线于点 Q ， 仍作 ∠ PDQ 的平分线 DE 交 BC 延长线于点 E ， 连接 PE ， 若 AB ∶ AP ＝ 3 ∶ 4 ， 请帮小明算出 △ DEP 的面积． (3) 解： ∵ AB ∶ AP ＝ 3 ∶ 4 ， AB ＝ 6 ， ∴ AP ＝ 8 ， BP ＝ 2 ， 由 (1) 知： △ ADP ≌△ CDQ ， 则 AP ＝ CQ ＝ 8 ， 由 (2) 知： PE ＝ QE ， 设 CE ＝ x ， 则 PE ＝ QE ＝ CQ － CE ＝ 8 － x ， 在 R t △ PEB 中 ， BP ＝ 2 ， BE ＝ 6 ＋ x ， PE ＝ 8 － x ， 由勾股定理得 2 2 ＋ (6 ＋ x) 2 ＝ (8 － x) 2 ， 解得 x ＝ 6 7 ， ∵ BP ∥ CD ， ∴ BM CM ＝ BP CD ， ∴ BM 6 － BM ＝ 2 6 ， ∴ BM ＝ 3 2 ， ∴ ME ＝ CM ＋ CE ＝ 6 － 3 2 ＋ x ＝ 6 － 3 2 ＋ 6 7 ＝ 75 14 ， ∴△ DEP 的面积为 S △ D EP ＝ S △ DME ＋ S △ PME ＝ 1 2 ·ME·DC ＋ 1 2 ·ME·PB ＝ 1 2 ·ME·(DC ＋ PB ) ＝ 1 2 × 75 14 ·(6 ＋ 2 ) ＝ 1 2 × 75 14 × (6 ＋ 2) ＝ 150 7