四川省眉山市2017年中考数学试题 9页

眉山市2017年初中学业水平暨高中阶段学校招生考试 数学试卷 一、选择题(36分)‎ ‎1．下列四个数中，比－3小的数是( )‎ A．0 B．1 C．－1 D．－5‎ ‎2．不等式－2x＞的解集是( )‎ A．x＜－ B． x＜－1 C． x＞－ D． x＞－1‎ ‎3．某微生物的直径为0.000 005 035m，用科学记数法表示该数为( )‎ A．5.035×10－6 B． 50.35×10－5 C． 5.035×106 D． 5.035×10－5‎ ‎4．如图所示的几何体的主视图是( )[来源:学+科+网]‎ ‎5．下列说法错误的是( )‎ A．给定一组数据，那么这组数据的平均数一定只有一个 B．给定一组数据，那么这组数据的中位数一定只有一个 C．给定一组数据，那么这组数据的众数一定只有一个 D．如果一组数据存在众数，那么该众数一定是这组数据中的某一个 ‎6．下列运算结果正确的是( )‎ A．－＝－ B．(－0.1)－2＝0.01 C．()2÷＝ D．(－m)3·m2＝－m6‎ ‎7．已知关于x，y的二元一次方程组的解为，则a－2b的值是( )‎ A．－2 B．2 C．3 D．－3‎ ‎8．“今有井径五尺，不知其深，立五尺木于井上，从木末望水岸，入径四寸，问井深几何？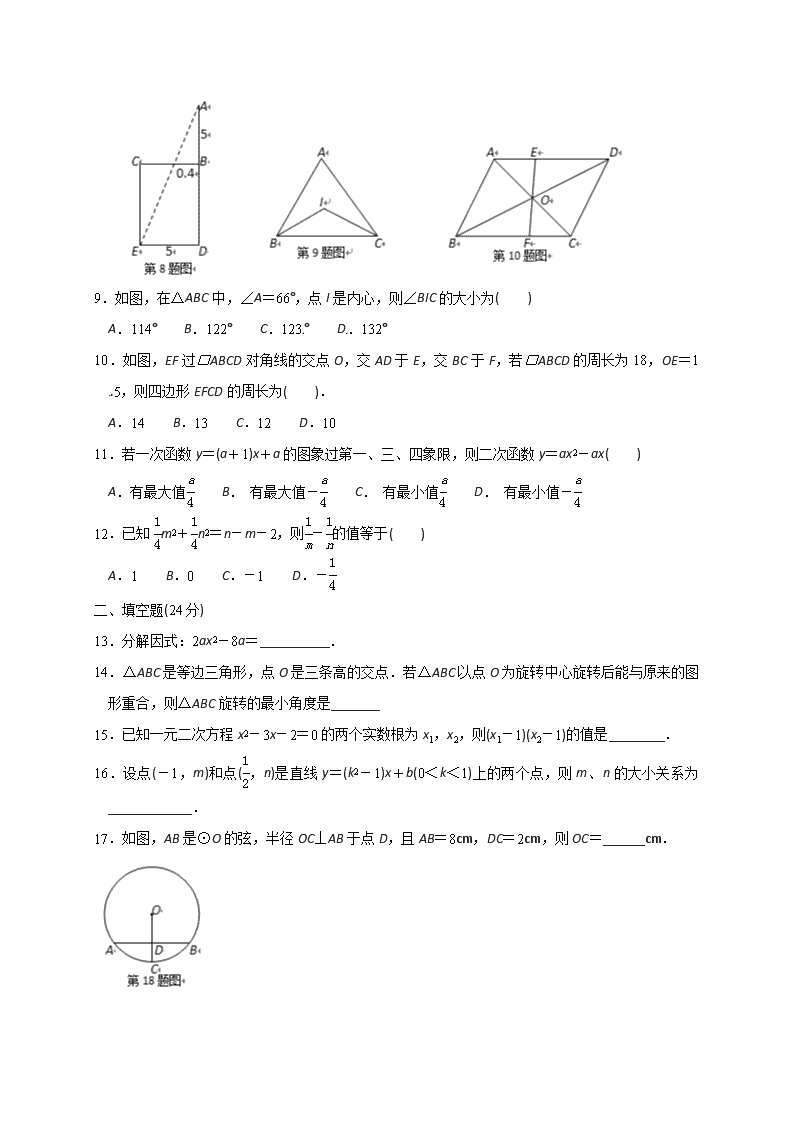”这是我国古代数学《九章算术》中的“井深几何”问题，它的题意可以由图获得，则井深为( )2‎ A．1.25尺 B．57.5尺 C．6.25尺 D．56.5尺 ‎9．如图，在△ABC中，∠A＝66°，点I是内心，则∠BIC的大小为( )‎ A．114° B．122° C．123° D．132°[来源:Z,xx,k.Com][来源:学§科§网Z§X§X§K]‎ ‎10．如图，EF过□ABCD对角线的交点O，交AD于E，交BC于F，若□ABCD的周长为18，OE＝1.5，则四边形EFCD的周长为( )．‎ A．14 B．13 C．12 D．10‎ ‎11．若一次函数y＝(a＋1)x＋a的图象过第一、三、四象限，则二次函数y＝ax2－ax( )‎ A．有最大值 B． 有最大值－ C． 有最小值 D． 有最小值－ ‎12．已知m2＋n2＝n－m－2，则－的值等于( )‎ A．1 B．0 C．－1 D．－ 二、填空题(24分)‎ ‎13．分解因式：2ax2－8a＝__________．‎ ‎14．△ABC是等边三角形，点O是三条高的交点．若△ABC以点O为旋转中心旋转后能与原来的图形重合，则△ABC旋转的最小角度是_______‎ ‎15．已知一元二次方程x2－3x－2＝0的两个实数根为x1，x2，则(x1－1)(x2－1)的值是________．‎ ‎16．设点(－1，m)和点(，n)是直线y＝(k2－1)x＋b(0＜k＜1)上的两个点，则m、n的大小关系为____________．‎ ‎17．如图，AB是⊙O的弦，半径OC⊥AB于点D，且AB＝8cm，DC＝2cm，则OC＝______cm．‎ ‎18．已知反比例函数y＝，当x＜－1时，y的取值范围为___________．‎ 三．解答题：(60分)‎ ‎19．(6分)先化简，再求值：(a＋3)2－2(3a＋4)，其中a＝－2．‎ ‎20．(6分)解方程:＋2＝．‎ ‎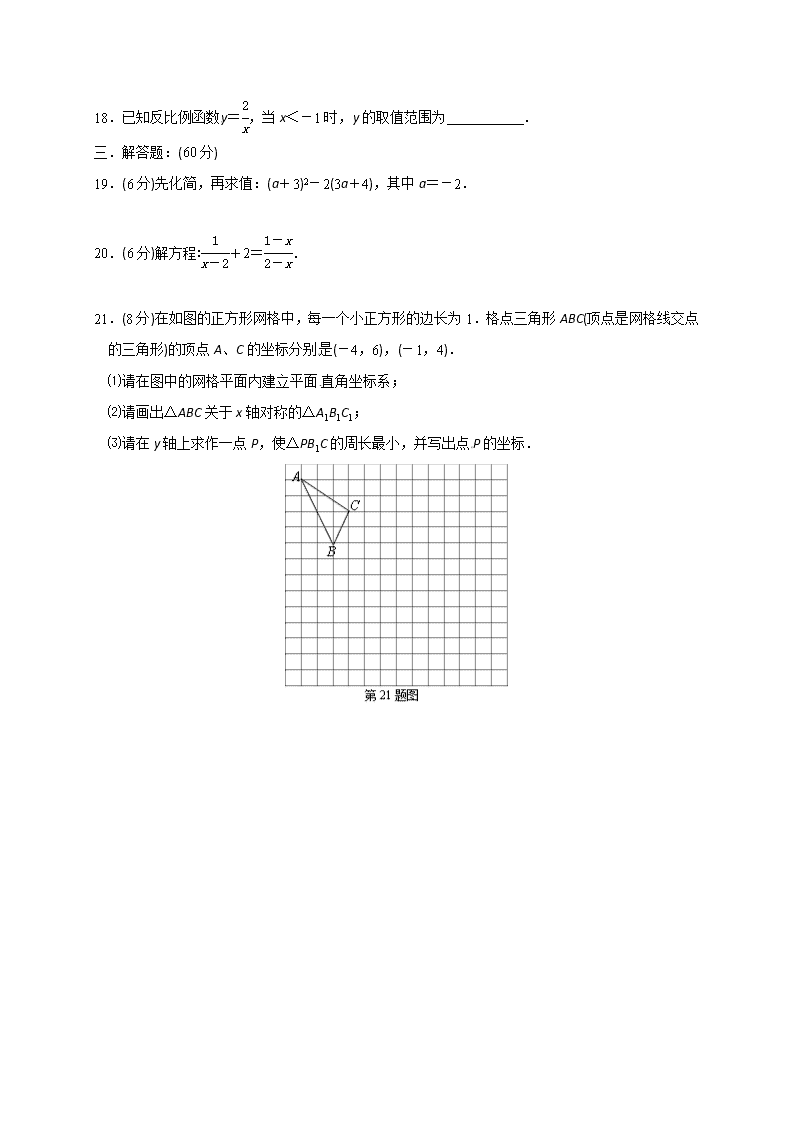21．(8分)在如图的正方形网格中，每一个小正方形的边长为1．格点三角形ABC(顶点是网格线交点的三角形)的顶点A、C的坐标分别是(－4，6)，(－1，4)．‎ ‎⑴请在图中的网格平面内建立平面直角坐标系；‎ ‎⑵请画出△ABC关于x轴对称的△A1B1C1；‎ ‎⑶请在y轴上求作一点P，使△PB1C的周长最小，并写出点P的坐标．‎ ‎22．(8分)如图，为了测得一棵树的高度AB，小明在D处用高为1m的测角仪CD，测得树顶A的仰角为45°，再向树方向前进10m，又测得树顶A的仰角为60°，求这棵树的高度AB．‎ ‎[来源:学科网]‎ ‎23．(9分)一个口袋中放有290个涂有红、黑、白三种颜色的质地相同的小球．若红球个数是黑球个数的2倍多40个．从袋中任取一个球是白球的概率是．‎ ‎⑴求袋中红球的个数；‎ ‎⑵求从袋中任取一个球是黑球的概率．‎ ‎24．(9分)东坡某烘焙店生产的蛋糕礼盒分为六个档次，第一档次(即最低档次)的产品每天生产76件，每件利润10元．调查表明：生产提高一个档次的蛋糕产品，该产品每件利润增加2元．‎ ‎⑴若生产的某批次蛋糕每件利润为14元，此批次蛋糕属第几档次产品；‎ ‎⑵由于生产工序不同，蛋糕产品每提高一个档次，一天产量会减少4件．若生产的某档次产品一天的总利润为1080元，该烘焙店生产的是第几档次的产品？‎ ‎25．(9分)如图，点E是正方形ABCD的边BC延长线上一点，连结DE，过顶点B作BF⊥DE，垂足为F，BF分别交AC于H，交BC于G．‎ ‎⑴求证：BG＝DE；‎ ‎⑵若点G为CD的中点，求的值．‎ ‎[来源:学科网]‎ ‎26．(11分)如图，抛物线y＝ax2＋bx－2与x轴交于A、B两点，与y轴交于C点，已知A(3，0)，且M(1，－)是抛物线上另一点．‎ ‎⑴求a、b的值；‎ ‎⑵连结AC，设点P是y轴上任一点，若以P、A、C三点为顶点的三角形是等腰三角形，求P点的坐标；‎ ‎⑶若点N是x轴正半轴上且在抛物线内的一动点(不与O、A重合)，过点N作NH∥AC交抛物线的对称轴于H点．设ON＝t，△ONH的面积为S，求S与t之间的函数关系式．‎