（鄂尔多斯专版）中考数学复习：圆的有关性质课件-43张 43页

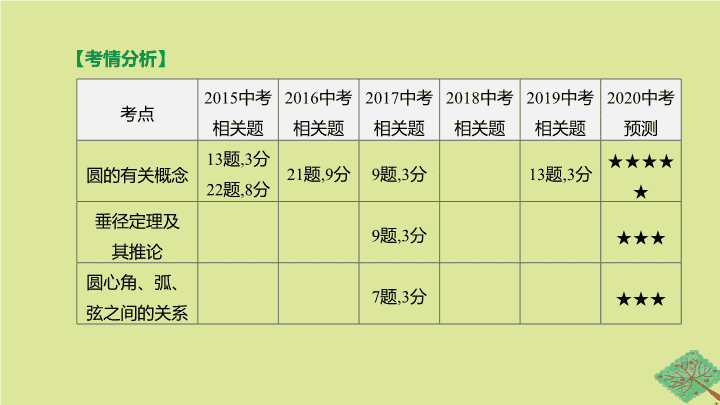
圆的有关性质 第六单元　圆 【 考情分析 】 考点 2015 中考 相关题 2016 中考 相关题 2017 中考 相关题 2018 中考 相关题 2019 中考 相关题 2020 中考 预测 圆的有关概念 13 题 ,3 分 22 题 ,8 分 21 题 ,9 分 9 题 ,3 分 13 题 ,3 分 ★★★★★ 垂径定理 及 其 推论 9 题 ,3 分 ★★★ 圆心角、弧、 弦之间的关系 7 题 ,3 分 ★★★ 考点 2015 中考 相关题 2016 中考 相关题 2017 中考 相关题 2018 中考 相关题 2019 中考 相关题 2020 中考 预测 圆周角定理 及其推论 22 题 ,8 分 7 题 ,3 分 21 题 ,9 分 16 题 ,3 分 ★★★★ 圆内接四边形 的性质定理 7 题 ,3 分 16 题 ,3 分 ★★★ ( 续表 ) 考点一　圆的有关概念及性质 考点聚焦 1 . 圆 : 在一个平面内 , 线段 OA 绕它固定的一个端点 O 旋转一周 , 另一个端点 A 所形成的图形叫做圆 . 其固定的端点 O 叫做 ① 　　　　 , 线段 OA 叫做 ② 　　　　 .  2 . 圆的对称性 : 圆既是 ③ 　　　 对称图形 , 又是 ④ 　　　　 对称图形 , 圆还具有旋转不变性 .  3 . 确定圆的条件 : 不在 ⑤ 　　 　　 点确定一个圆 .  半径 圆心 轴 中心 同一条直线上的三个 概念 示例 弧 　 圆上任意两点间的部分叫做圆弧 , 简称弧 . 大于半圆的弧叫 ⑥ 　　　 , 小于半圆的弧叫 ⑦ 　　　   弦 　 连接圆上任意两点的线段叫做弦 , 经过圆心的弦叫做 ⑧ 　　　   如弦 AC , 直径 AB 圆心角 顶点在圆心的角 如 ∠ AOC 圆周角 　 顶点在圆上 , 并且两边都与圆相交的角 如 ∠ ABC 4 . 圆的有关概念 优弧 劣弧 直径 考点二　圆心角、弧、弦之间的关系 定理 在 同圆或等圆中 , 相等的圆心角所对的 ⑨ 　　 相等 , 所对的 ⑩ 　　 也 相等 示例 推论 　 在同圆或等圆中 , 如果两个圆心角﹑两条弧或两条弦中有一组量相等 , 那么它们所对应的其余各组量也分别相等 弧 弦 考点三　垂径定理及其推论 垂径定理 　 垂直于弦的直径 ⑪ 　　　　 , 并且平分弦所对的两条弧     示例 推论 (1) 平分弦 ( 不是直径 ) 的直径 ⑫ 　　　 于弦 , 并且平分弦所对的两条弧 ;  (2) 弦的 ⑬ 　 　　　 经过圆心 , 并且平分弦所对的两条弧 ;  (3) 平分弦所对的一条弧的直径 , 垂直平分弦 , 并且平分弦所对的另一条弧 垂直 垂直平分线 平分弦 ( 续表 ) 总结 　 简言之 , 对于 ① 过圆心、 ② 垂直弦、 ③ 平分弦 ( 不是直径 ) 、 ④ 平分弦所对的优弧、 ⑤ 平分弦所对的劣弧中的任意两条结论成立 , 那么其他的结论也成立 考点四　圆周角定理及其推论 圆周角定理 　 一条弧所对的圆周角等于它所对的圆心角的 ⑭ 　　　   常见图形 推论 1 同弧或等弧所对的圆周角 ⑮ 　 　   推论 2 　 半圆 ( 或直径 ) 所对的圆周角是 ⑯ 　　　 ,90° 的圆周角所对的弦是 ⑰ 　　　   一半 相等 直径 直角 考点五　圆内接四边形的性质 圆内接四边形的对角 ⑱ 　　　　 .  [ 拓展 ] 圆内接四边形的任意一个外角等于它的内对角 , 如图 25-1, ∠ ABE = ∠ D. 图 25-1 互补 题组一　必会题 对点演练 A 图 25-2 2 . 如图 25-3, 四边形 ABCD 为☉ O 的内接四边形 , 已知∠ BOD =100°, 则∠ BCD 的度数为 ( 　　 ) A . 50° B . 80° C . 100° D . 130° 图 25-3 D 3 . 如图 25-4, 已知 AB 是☉ O 的直径 , ∠ D =40°, 则∠ CAB 的度数为 ( 　　 ) A . 20° B . 40° C . 50° D . 70° 图 25-4 C 图 25-5 [ 答案 ] A 　 【 失分点 】 忽视圆中的一条弦所对的弧有两条 , 所对的圆周角也有两个 ; 构图时存在多种情况时考虑不全面 . 题组二　易错题 5 . [2018· 通辽 ] 已知☉ O 的半径为 10, 圆心 O 到弦 AB 的距离为 5, 则弦 AB 所对圆周角的度数是 ( 　　 ) A . 30° B . 60° C . 30° 或 150° D . 60° 或 120° [ 答案 ] D 　 [ 答案 ] C 　 [ 答案 ] 2 或 14 　 考向一　垂径定理及其推论 例 1 [ 九上 P89 习题 24 . 1 第 8 题改编 ] 如图 25-6 是一个隧道的横截面 , 它的形状是以点 O 为圆心的圆的一部分 . 如果 M 是☉ O 中弦 CD 的中点 , EM 经过圆心 O 交☉ O 于点 E , 并且 CD =4 m, EM =6 m, 则☉ O 的半径为 　　　　 m .  图 25-6 【 方法点析 】 圆中涉及线段的计算时 , 往往要作弦的垂线 , 连接这条弦的端点与圆心 , 从而构造直角三角形 , 利用垂径定理和勾股定理进行计算 , 多条线段未知时可设未知数列方程求解 . | 考向精练 | 图 25-7 [ 答案 ] C 　 图 25-8 [ 答案 ] D 　 考向二　圆周角定理及其推论 图 25-9 [ 答案 ] 2 　 | 考向精练 | 图 25-10 [ 答案 ] B 　 2 . [2019· 赤峰 ] 如图 25-11, AB 是☉ O 的弦 , OC ⊥ AB 交☉ O 于点 C , 点 D 是☉ O 上一点 , ∠ ADC =30°, 则∠ BOC 的度数为 ( 　　 ) A . 30° B . 40° C . 50° D . 60° 图 25-11 [ 答案 ] D 　 考向三　圆内接四边形的性质 例 3 [2017· 淮安 ] 如图 25-12, 在圆内接四边形 ABCD 中 , 若∠ A , ∠ B , ∠ C 的度数之比为 4 ∶ 3 ∶ 5, 则∠ D 的度数是 　　　　 ° .  图 25-12 [ 答案 ] 120 　 [ 解析 ] ∵∠ A , ∠ B , ∠ C 的度数之比为 4 ∶ 3 ∶ 5, ∴设∠ A =4 x , 则∠ B =3 x , ∠ C =5 x. ∵四边形 ABCD 是圆内接四边形 , ∴∠ A + ∠ C =180°, 即 4 x +5 x =180°, 解得 x =20°, ∴∠ B =3 x =60°, ∴∠ D =180°-60°=120° . | 考向精练 | [2019· 天水 ] 如图 25-13, 四边形 ABCD 是菱形 , ☉ O 经过点 A , C , D , 与 BC 相交于点 E , 连接 AC , AE. 若∠ D =80°, 则∠ EAC 的度数为 ( 　　 ) A . 20° 　　 B . 25° C . 30° 　　 D . 35° 图 25-13 [ 答案 ] C 　 考向四　圆的综合运用 图 25-14 解 :(1) 证明 : 由题意可得∠ BPC = ∠ BAC , ∠ APC = ∠ ABC. ∵∠ BPC = ∠ APC =60°, ∴∠ BAC = ∠ ABC =60°, ∴ △ ABC 是等边三角形 . 图 25-14 | 考向精练 | 图 25-15 解 :(1) 证明 : 连接 AE. ∵∠ BAC =90°, ∴ CF 是☉ O 的直径 . ∵ AC = EC , ∴ CF ⊥ AE. ∵ AD 为☉ O 的直径 , ∴∠ AED =90°, 即 GD ⊥ AE , ∴ CF ∥ DG. ∵ AD 为☉ O 的直径 , ∴∠ ACD =90°, ∴∠ ACD + ∠ BAC =180°, ∴ AB ∥ CD , ∴四边形 DCFG 为平行四边形 . 图 25-15