初中数学中考复习课件章节考点专题突破：第七章 图形的变化自我测试 23页

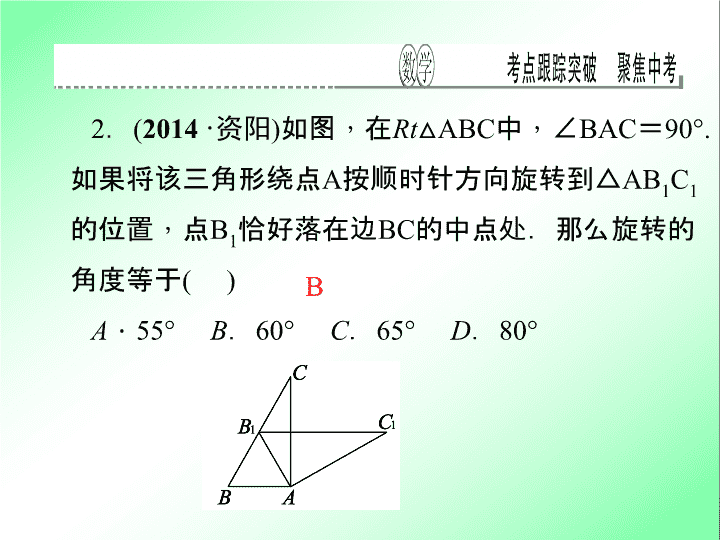
第七章　图形的变化自我测试 一、选择题 ( 每小题 4 分 ， 共 32 分 ) 1 ． ( 2014 · 临夏州 ) 下列图形中 ， 是轴对称图形又是中心对称图形的是 ( ) D 2 ． ( 2014 · 资阳 ) 如图 ， 在 Rt △ ABC 中 ， ∠ BAC ＝ 90°. 如果将该三角形绕点 A 按顺时针方向旋转到 △ AB 1 C 1 的位置 ， 点 B 1 恰好落在边 BC 的中点处．那么旋转的角度等于 ( ) A ． 55° B ． 60° C ． 65° D ． 80° B 3 ． ( 2014· 毕节 ) 如图 ， △ ABC 中 ， AE 交 BC 于点 D ， ∠ C ＝ ∠ E ， AD ∶ DE ＝ 3 ∶ 5 ， AE ＝ 8 ， BD ＝ 4 ， 则 DC 的 长等于 ( ) A . 15 4 B . 12 5 C . 20 3 D . 17 4 A 4 ． ( 2014· 兰州 ) 如图 ， 在 Rt △ ABC 中 ， ∠ C ＝ 90 ° ， BC ＝ 3 ， AC ＝ 4 ， 那么 cos A 的值等于 ( ) A . 3 4 B . 4 3 C . 3 5 D . 4 5 D 5 ． ( 2014 · 东营 ) 下列关于位似图形的表述： ① 相似图形一定是位似图形 ， 位似图形一定是相似图形； ② 位似图形一定有位似中心； ③ 如果两个图形是相似图形 ， 且每组对应点的连线所在的直线都经过同一个点 ， 那么 ， 这两个图形是位似图形； ④ 位似图形上任意两点与位似中心的距离之比等于位似比． 其中正确命题的序号是 ( ) A ． ②③ B ． ①② C ． ③④ D ． ②③④ A 6 ． ( 2013 · 泰安 ) 在如图所示的单位正方形网格中 ， △ ABC 经过平移后得到 △ A 1 B 1 C 1 ， 已知在 AC 上一点 P(2.4 ， 2) 平移后的对应点为 P 1 ， 点 P 1 绕点 O 逆时针旋转 180° ， 得到对应点 P 2 ， 则 P 2 点的坐标为 ( ) A ． (1.4 ， － 1) B ． (1.5 ， 2) C ． (1.6 ， 1) D ． (2.4 ， 1) C 7 ． ( 2014· 襄阳 ) 如图 ， 在矩形 ABCD 中 ， 点 E ， F 分别在 边 AB ， BC 上 ， 且 AE ＝ 1 3 AB ， 将矩形沿直线 EF 折叠 ， 点 B 恰好落在 AD 边上的点 P 处 ， 连接 BP 交 EF 于点 Q ， 对于下列结论： ① EF ＝ 2BE ； ② PF ＝ 2PE ； ③ FQ ＝ 4EQ ； ④△ PBF 是等边三角形． 其中正确的是 ( ) A ． ①② B ． ②③ C ． ①③ D ． ①④ D 8 ． ( 2013· 青岛 ) 如图 ， △ ABO 缩小后变为 △ A ′ B ′ O ， 其中 A ， B 的对应点分别为 A ′ ， B ′ ， A ′ ， B ′ 均在图中格点上 ， 若线段 AB 上有一点 P ( m ， n ) ， 则点 P 在 A ′ B ′ 上的对应点 P ′ 的坐标为 ( ) A ． ( m 2 ， n ) B ． ( m ， n ) C ． ( m ， n 2 ) D ． ( m 2 ， n 2 ) D 二、填空题 ( 每小题 6 分 ， 共 24 分 ) 9 ． ( 2013 · 雅安 ) 如图 ， 在 ▱ ABCD 中 ， 点 E 在 AB 上 ， CE ， BD 交于点 F ， 若 AE ∶ BE ＝ 4 ∶ 3 ， 且 BF ＝ 2 ， 则 DF ＝ ____ ． 10 ． ( 2014 · 威海 ) 如图 ， 有一直角三角形纸片 ABC ， 边 BC ＝ 6 ， AB ＝ 10 ， ∠ ACB ＝ 90° ， 将该直角三角形纸片沿 DE 折叠 ， 使点 A 与点 C 重合 ， 则四边形 DBCE 的周长为 ____ ． 18 11 ． ( 2014· 苏州 ) 如图 ， 在 △ ABC 中 ， AB ＝ AC ＝ 5 ， BC ＝ 8. 若 ∠ BPC ＝ 1 2 ∠ BAC ， 则 tan ∠ BPC ＝ __ __ ． 12 ． ( 2014 · 遵义 ) “ 今有邑 ， 东西七里 ， 南北九里 ， 各开中门 ， 出东门一十五里有木 ， 问：出南门几何步而见木？ ” 这段话摘自 《 九章算术 》 ， 意思是说：如图 ， 矩形 ABCD ， 东边城墙 AB 长 9 里 ， 南边城墙 AD 长 7 里 ， 东门点 E 、南门点 F 分别是 AB ， AD 的中点 ， EG ⊥ AB ， FH ⊥ AD ， EG ＝ 15 里 ， HG 经过 A 点 ， 则 FH ＝ ____ 里． 1.05 三、解答题 ( 共 44 分 ) 13 ． (10 分 ) ( 2014 · 凉山 ) 如图所示 ， 正方形网格中 ， △ ABC 为格点三角形 ( 即三角形的顶点都在格点上 ) ． (1) 把 △ ABC 沿 BA 方向平移后 ， 点 A 移到点 A 1 ， 在网格中画出平移后得到的 △ A 1 B 1 C 1 ； (2) 把 △ A 1 B 1 C 1 绕点 A 1 按逆时针方向旋转 90° ， 在网格中画出旋转后的 △ A 1 B 2 C 2 ； (3) 如果网格中小正方形的边长为 1 ， 求点 B 经过 (1)(2) 变换的路径总长． 14 ． ( 10 分 ) ( 2013· 遵义 ) 如图 ， 将一张矩形纸片 ABCD 沿直线 MN 折叠 ， 使点 C 落在点 A 处 ， 点 D 落在点 E 处 ， 直线 MN 交 BC 于点 M ， 交 AD 于点 N. ( 1 ) 求证： CM ＝ CN ； ( 2 ) 若 △ CMN 的面积与 △ CDN 的面积比为 3 ∶ 1 ， 求 MN DN 的值 ． 解： ( 1 ) 证明：由折叠的性质可得 ∠ ANM ＝ ∠ CNM ， ∵ 四边形 ABCD 是矩形 ， ∴ AD ∥ BC ， ∴∠ ANM ＝ ∠ CMN ， ∴∠ CMN ＝ ∠ CNM ， ∴ CM ＝ CN ( 2 ) 解：过点 N 作 NH ⊥ BC 于点 H ， 则四边形 NHCD 是矩形 ， ∴ HC ＝ DN ， NH ＝ DC ， ∵△ CMN 的面积与 △ CDN 的面积比为 3 ∶ 1 ， ∴ S △ CMN S △ CDN ＝ 1 2 ·MC·NH 1 2 ·ND·NH ＝ MC ND ＝ 3 ， ∴ MC ＝ 3ND ＝ 3HC ， ∴ MH ＝ 2HC ， 设 DN ＝ x ， 则 HC ＝ x ， MH ＝ 2x ， ∴ CM ＝ 3x ＝ CN ， 在 Rt △ CDN 中 ， DC ＝ CN 2 － DN 2 ＝ 2 2 x ， ∴ HN ＝ 2 2 x ， 在 Rt △ MNH 中 ， MN ＝ MH 2 ＋ HN 2 ＝ 2 3 x ， ∴ MN DN ＝ 2 3 x x ＝ 2 3 1 5 ． (12 分 ) ( 2014· 兰州 ) 如图 ， 在电线杆上的 C 处引拉线 CE ， CF 固定电线杆 ， 拉线 CE 和地面成 60 ° 角 ， 在离电 线杆 6 米的 B 处安置测角仪 ， 在 A 处测得电线杆上 C 处 的仰角为 30 ° ， 已知测角仪高 AB 为 1.5 米 ， 求拉线 CE 的长． ( 结果保留根号 ) 解： 过点 A 作 AH ⊥ CD ， 垂足为点 H ， 由题意可知四边形 ABDH 为矩形 ， ∠ CAH ＝ 30 ° ， ∴ AB ＝ DH ＝ 1.5 ， BD ＝ AH ＝ 6 ， 在 Rt △ ACH 中 ， tan ∠ CAH ＝ CH AH ， ∴ CH ＝ AH· tan ∠ CAH ＝ 6 tan 30 ° ＝ 6 × 3 3 ＝ 2 3 ( 米 ) ， ∵ DH ＝ 1.5 ， ∴ CD ＝ 2 3 ＋ 1.5 ， 在 Rt △ CDE 中 ， ∵∠ CED ＝ 60 ° ， sin ∠ CED ＝ CD CE ， ∴ CE ＝ CD sin 60 ° ＝ 2 3 ＋ 1.5 3 2 ＝ (4 ＋ 3 )( 米 ) ， 答：拉线 CE 的长为 (4 ＋ 3 ) 米 16 ． (12 分 ) ( 2013 · 徐州 ) 如图 ， 在 Rt △ ABC 中 ， ∠ C ＝ 90° ， 翻折 ∠ C ， 使点 C 落在斜边 AB 上某一点 D 处 ， 折痕为 EF( 点 E ， F 分别在边 AC ， BC 上 ) ． (1) 若 △ CEF 与 △ ABC 相似． ① 当 AC ＝ BC ＝ 2 时 ， AD 的长为 ____ ； ②当 AC ＝ 3 ， BC ＝ 4 时 ， AD 的长为 ____ ； 1.8 ( Ⅱ ) 若 CF ∶ CE ＝ 3 ∶ 4 ， 如图 ③ 所示 ． ∵△ CEF ∽△ CBA ， ∴∠ CEF ＝ ∠ B. 由折叠性质可知 ， ∠ CEF ＋ ∠ ECD ＝ 90 ° ， 又 ∵∠ A ＋ ∠ B ＝ 90 ° ， ∴∠ A ＝ ∠ ECD ， ∴ AD ＝ CD. 同理可得 ∠ B ＝ ∠ FCD ， CD ＝ BD ， ∴ 此时 AD ＝ 1 2 AB ＝ 1 2 × 5 ＝ 2.5. 综上所述 ， 当 AC ＝ 3 ， BC ＝ 4 时 ， AD 的长为 1.8 或 2.5 (2) 当点 D 是 AB 的中点时 ， △ CEF 与 △ ABC 相似吗？请说明理由．