中考数学第一轮复习导学案反比例函数 9页

- 1 - x y O 第 1 题 反比例函数 ◆ 课前热身 1.反比例函数 1y x （x＞0）的图象如图所示，随着 x 值的 增大，y 值（ ） A．增大 B．减小 C．不变 D．先减小后增大 2.已知反比例函数 ky x 的图象经过点(2 3)， ，则此函数的关系式是 ． 3.一个直角三角形的两直角边长分别为 yx， ，其面积为 2，则 y 与 x 之间的关系用图象表 示大致为（ ） 4.如图，函数 yx 与 4y x 的图象交于 A、B 两点，过点 A 作 AC 垂直于 y 轴，垂足为 C，则 ABC△ 的面积为 ． 【参考答案】 1. B 2. 6y x 3. C 4.4 ◆考点聚焦 知识点 反比例函数意义；反比例函数 反比例函数图象；反比例函数性质；待定系数法确定函数解 析式. 大纲要求 理解反比例函数的性质，掌握如何确定反比例函数表达式、反比例函数图象的画法、用反 比例函数解决某些实际问题。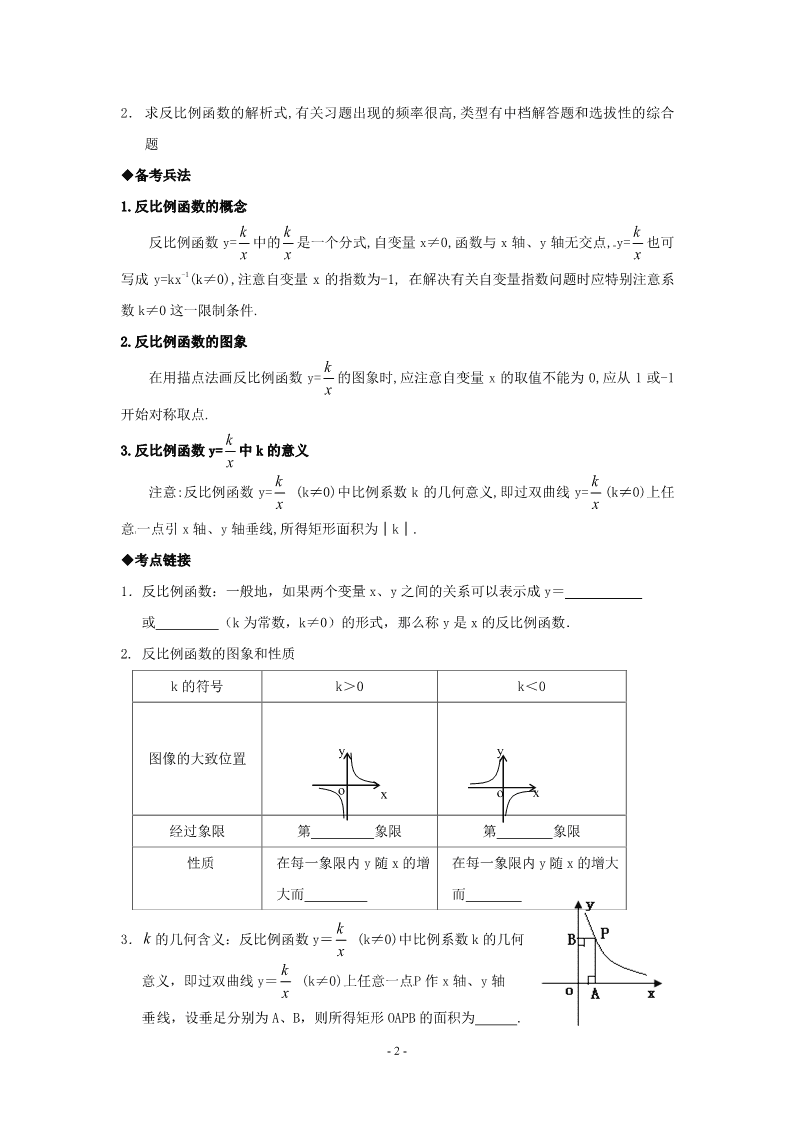 考查重点与常见题型 1． 考查反比例函数的定义、图象和性质，有关试题常出现在选择题中 A B C D y x O O O O - 2 - 2． 求反比例函数的解析式,有关习题出现的频率很高,类型有中档解答题和选拔性的综合 题 ◆备考兵法 1.反比例函数的概念 反比例函数 y= k x 中的 k x 是一个分式,自变量 x≠0,函数与 x 轴、y 轴无交点, y= k x 也可 写成 y=kx-1(k≠0),注意自变量 x 的指数为-1, 在解决有关自变量指数问题时应特别注意系 数 k≠0 这一限制条件. 2.反比例函数的图象 在用描点法画反比例函数 y= k x 的图象时,应注意自变量 x 的取值不能为 0,应从 1 或-1 开始对称取点. 3.反比例函数 y= k x 中 k 的意义 注意:反比例函数 y= k x (k≠0)中比例系数 k 的几何意义,即过双曲线 y= k x (k≠0)上任 意一点引 x 轴、y 轴垂线,所得矩形面积为│k│. ◆考点链接 1．反比例函数：一般地，如果两个变量 x、y 之间的关系可以表示成 y＝ 或 （k 为常数，k≠0）的形式，那么称 y 是 x 的反比例函数． 2. 反比例函数的图象和性质 3． k 的几何含义：反比例函数 y＝ (k≠0)中比例系数 k 的几何 意义，即过双曲线 y＝ (k≠0)上任意一点P 作 x 轴、y 轴 垂线，设垂足分别为 A、B，则所得矩形 OAPB 的面积为 . k 的符号 k＞0 k＜0 图像的大致位置 经过象限 第 象限 第 象限 性质 在每一象限内 y 随 x 的增 大而 在每一象限内 y 随 x 的增大 而 o y x y x o - 3 - ◆ 典例精析 例 1.（湖南娄底）市一小数学课外兴趣小组的同学每人制作一个面积为 200cm2 的矩形学具 进行展示. 设矩形的宽为 xcm，长为 ycm，那么这些同学所制作的矩形长 y（cm）与宽 x（cm） 之间的函数关 系的图象大致是 ( ) 【分析】根据题意列出函数关系式 200y x ，函数是反比例函数，所以排除 C 和 D,因为 K ＞0，所以函数位于一、三象限，又因为 x＞0，y＞0,所以函数位于第一象限，故选 A. 【答案】A 例 2（新疆）若梯形的下底长为 x ，上底长为下底长的 1 3 ，高为 y ，面积为 60，则 与 的 函数关系是____________．（不考虑 的取值范围） 【分析】根据题意知上底长 1 3 x ，梯形面积= 11( ) 6023x x y   ，所以 90y x 【答案】 例 3（内蒙古包头）如图，已知一次函数 1yx的图象与反比例函数 ky x 的图象在第一 象限相交于点 A ，与 x 轴相交于点C AB x， ⊥ 轴于点 B ， AOB△ 的面积为 1，则 AC 的 长为 （保留根号）． 【答案】 22 【解析】本题考查函数图象交点坐标的求法及反比例函数的比例系数 k 与其图象上的点与原 点所连的线段、坐标轴、向坐标轴作垂线所围 成的直角三角形面积 S 的关系，即 1 2Sk ， 由 2k  ，且图象在第一象限内，所以 2k  ，由 1 2 yx y x   得点 A 坐标为(1,2)，而 1yx y O x A C B - 4 - 与 x 轴的交点坐标为(-1,0)，所以 AB=2，BC=2。由勾股定理得 222 2 2 2AC    ◆迎考精炼 一、选择题 1.（山西）反比例函数 ky x 的图象经过点 23 ， ，那么 k 的值是（ ） A． 3 2 B． 2 3 C． 6 D．6 2.（湖南娄底）一次函数 y=kx+b 与反比例函数 的 图象如图所示，则下列说法正确的是（ ） A．它们的函数值 y 随着 x 的增大而增大 B．它们的函数值 y 随着 x 的增大而减小 C．k＜0 D．它们的自变量 x 的取值为全体实数 3.（广西南宁）在反比例函数 1 ky x  的图象的每一条曲线上， yx都随 的增大而增大， 则 k 的值可以是（ ） A． 1 B．0 C．1 D．2 4.（四川泸州）已知反比例函数 x ky  的图象经过点 P(一 l，2)，则这个函数的图象位于 （ ） A．第二、三象限 B．第一、三象限 C．第三、四象限 D．第二、四象限 5.（湖北恩施）一张正方形的纸片，剪去两个一样的小矩形得到一个“ E ”图案 ，如图所 示，设小矩形的长和宽分别为 x 、 y ，剪去部分的面积为 20，若 2 10x≤ ≤ ，则 与 的 函数图象是（ ） 6. (山东潍坊)在同一平面直角坐标系中，反比例函数 8y x 与一次函数 2yx   交于 AB、 两点，O 为坐标原点，则 AOB△ 的面积为（ ） 2 10 5 O x y 2 10 5 O x y 2 10 10 O x y 2 10 10 O x y y x 12 2 2 A． B． C． D． 12 - 5 - A．2 B．6 C．10 D．8 二、填空题 1.（浙江台州）请你写出一个图象在第一、三象限的反比例函数． 答： ． 2.（湖北仙桃）如图，已知双曲线 )0k(x ky ＞ 经过直角三角形OAB 斜边 OB 的中点 D，与直 角边 AB 相交于点 C．若△OBC 的面积为 3，则 k＝____________． 3．（ 广西柳州）反比例函数 x my 1 的图象经过点（2，1），则 m 的值是 ． 4.（河南）点 A(2，1)在反比例函数 y k x 的图像上，当 1﹤x﹤4 时，y 的取值范围 是 . 5．（ 江西）函数    12 4 0y x x y xx  ≥0 ， 的图象如图所示，则结论： ①两函数图象的交点 A 的坐标为 22， ； ②当 2x  时， 21yy ； ③当 1x  时， 3BC  ； ④当 x 逐渐增大时， 1y 随着 x 的增大而增大， 2y 随着 的增大而减小． 其中正确结论的序号是 ． y x O A B P C D - 6 - 6. (2009 年黑龙江牡丹江)如图，点 A 、 B 是双曲线 3y x 上的点，分别经过 、 两点 向 x 轴、 y 轴作垂线段，若 1S 阴影 ，则 12SS ． 7．（ 甘肃白银）反比例函数的图象经过点 P（ 2 ，1），则这个函数的图象位于 第 象限． 8.（湖南衡阳）如图，四边形 OABC 是边长为 1 的正方形，反比例函数 x ky  的图象过点 B， 则 k 的值为________． x y A B O 1S 2S 6 题图 O 1yx x A B C 1x  4y x y - 7 - 三、解答题 1. (宁夏自治区)已知正比例函数 1y k x 1( 0)k  与反比例函数 2 2( 0)kykx的图象交于 AB、 两点，点 A 的坐标为(21)， ． （1）求正比例函数、反比例函数的表达式； （2）求点 B 的坐标． 2.（四川宜宾）已知：如图，在平面直角坐标系 x O y 中，Rt△OCD 的一边 OC 在 轴上，∠ C=90°，点 D 在第一象限，OC=3，DC=4，反比例函数的图象经过 OD 的中点 A． （1）求该反比例函数的解析式； （2）若该反比例函数的图象与 Rt△OCD 的另一边 DC 交于点 B，求过 A、B 两点的直线的解 析式． 3.（ 山东枣庄） 为预防“手足口病”，某校对教室进行“药熏消毒”．已知药物燃烧阶段， 室内每立方米空气中的含药量 y（mg）与燃烧时间 x（分钟）成正比例；燃烧后，y 与 x 成 反比例（如图所示）．现测得药物 10 分钟燃烧完，此时教室内每立方米空气含药量为 8 mg．根 据以上信息，解答下列问题： （1）求药物燃烧时 y 与 x 的函数关系式； （2）求药物燃烧后 y 与 x 的函数关系式； （3）当每立方米空气中含药量低于 1.6 mg 时，对人体无毒害作用．那么从消毒开始， 经多长时间学生才可以返回教室？ O 8 10 x (分钟) y (mg) - 8 - 【参考答案】 一、选择题 1. C 2.C 3. D 4. D 5.A 6. B 二、填空题 1. xy 1 （答案不唯一） 2.2 3.1 4. 22 1＜y＜ 5.①③④ 6.4 7.二、四 8.-1 三、解答题 1.解：（1）把点 (21)A ，分别代入 1y k x 与 2ky x 得 1 1 2k  ， 2 2k  ． 正比例函数、反比例函数的表达式为： 12 2y x y x， ． （2）由方程组 1 2 2 yx y x     得 1 1 2 1 x y    ， 2 2 2 1 x y    ． B 点坐标是( 2, 1)． 2.(1)由题意得，点 A 的坐标是(1.5, 2), 该反比例函数的解析式为 y= x 3 . (2)把 x=3 代入 y=1. 点 B 的坐标是(3,1). 设过 A、B 两点的直线的解析式为: bkxy  ,则      .5.12 ,31 bk bk 解得      .3 ,3 2 b k 设过 A、B 两点的直线的解析式为: 33 2  xy . 3.（1）设药物燃烧阶段函数解析式为 11( 0)y k x k，由题意，得 18 10k ， 1 4 5k  ． ∴此阶段函数解析式为 4 5yx (0≤x＜10)． （2）设药物燃烧结束后函数解析式为 2 2( 0)kykx，由题意，得 - 9 - 28 10 k ， 2 80k  ． ∴此阶段函数解析式为 80y x （x≥10）． （3）当 y＜1.6 时，得 80 1.6x  ． ∵ 0x  ， ∴1.6 80x  ， 50x  ． ∴从消毒开始经过 50 分钟学生才返可回教室．