鄂尔多斯专版2020中考数学复习方案基础解答组合限时练07试题 10页

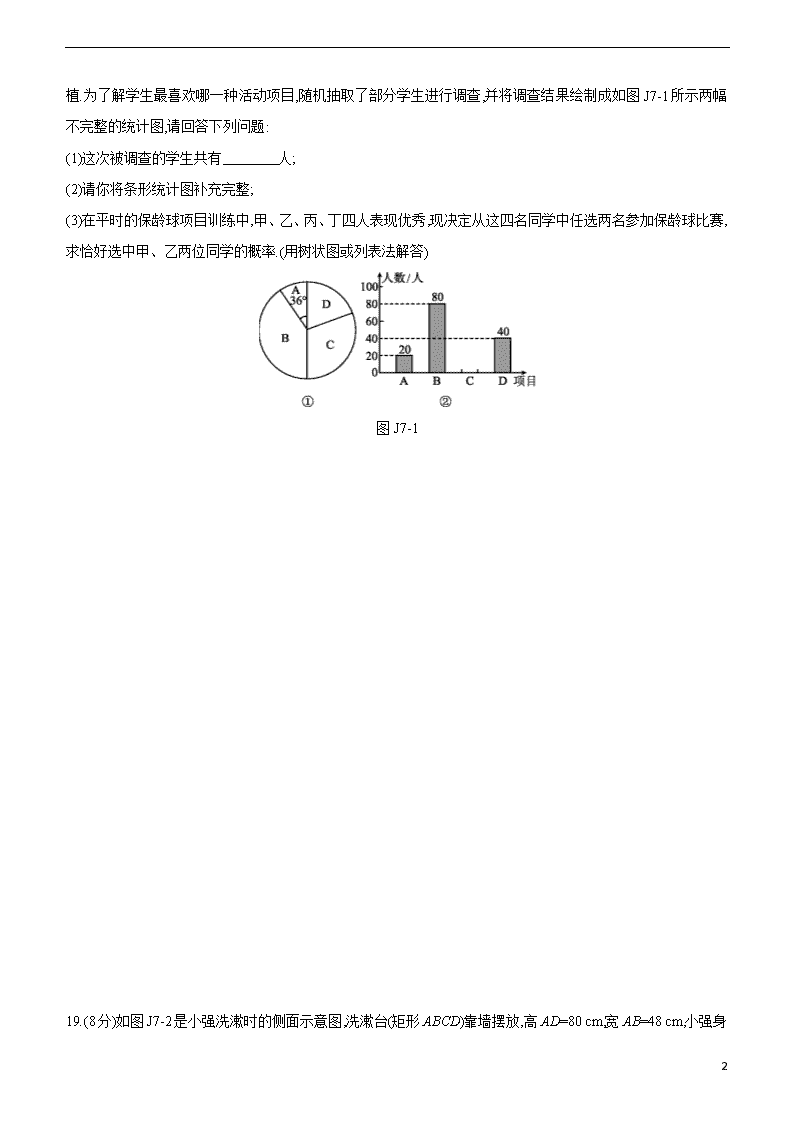
基础解答组合限时练(七)‎ 限时:40分钟　满分:49分 ‎17.(8分)(1)计算:2-1-2cos30°+|-‎12‎|+(3.14-π)0.‎ ‎(2)先化简,再求值:a‎2‎‎-2a+1‎a‎2‎‎-4‎÷a-1‎a-2‎‎+‎‎1‎a+2‎,其中a=|1-‎3‎|-tan60°+‎1‎‎2‎-1.‎ ‎18.(9分)某学校为了丰富学生的课余生活,决定开设以下体育课外活动项目:A.版画;B.保龄球;C.航模;D.园艺种 10‎ 植.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成如图J7-1所示两幅不完整的统计图,请回答下列问题:‎ ‎(1)这次被调查的学生共有　　　　人; ‎ ‎(2)请你将条形统计图补充完整;‎ ‎(3)在平时的保龄球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加保龄球比赛,求恰好选中甲、乙两位同学的概率.(用树状图或列表法解答)‎ 图J7-1‎ ‎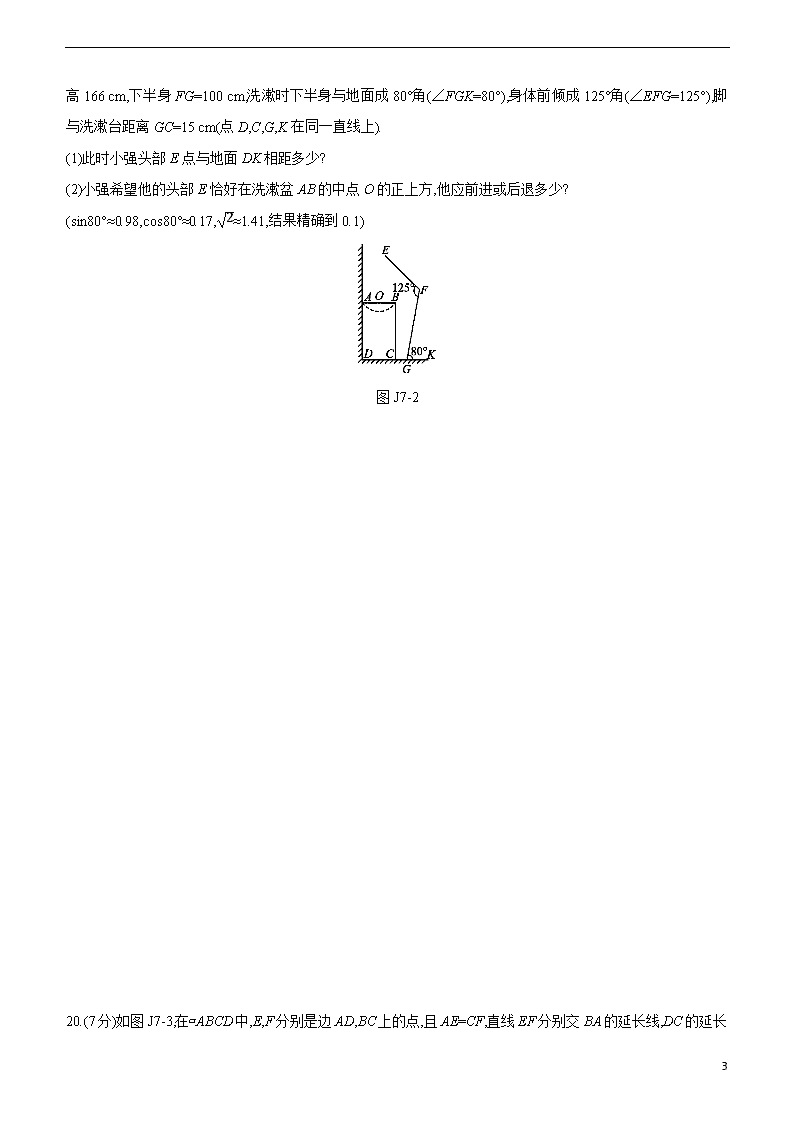19.(8分)如图J7-2是小强洗漱时的侧面示意图,洗漱台(矩形ABCD)靠墙摆放,高AD=80 cm,宽AB=48 cm,小强身 10‎ 高166 cm,下半身FG=100 cm,洗漱时下半身与地面成80°角(∠FGK=80°),身体前倾成125°角(∠EFG=125°),脚与洗漱台距离GC=15 cm(点D,C,G,K在同一直线上).‎ ‎(1)此时小强头部E点与地面DK相距多少?‎ ‎(2)小强希望他的头部E恰好在洗漱盆AB的中点O的正上方,他应前进或后退多少?‎ ‎(sin80°≈0.98,cos80°≈0.17,‎2‎≈1.41,结果精确到0.1)‎ 图J7-2‎ ‎20.(7分)如图J7-3,在▱ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线,DC的延长 10‎ 线于点G,H,交BD于点O.‎ ‎(1)求证:△ABE≌△CDF.‎ ‎(2)连接DG,若DG=BG,则四边形BEDF是什么特殊四边形?请说明理由.‎ 图J7-3‎ ‎21.(8分)如图J7-4,AC是☉O的直径,点D是☉O上一点,☉O的切线CB与AD的延长线交于点B,点F是直径AC 10‎ 上一点,连接DF并延长交☉O于点E,连接AE.‎ ‎(1)求证:∠ABC=∠AED;‎ ‎(2)连接BF,若AD=‎32‎‎5‎,AF=6,tan∠AED=‎4‎‎3‎,求BF的长.‎ 图J7-4‎ ‎22.(9分)为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大 10‎ 学毕业生自主销售,成本价与出厂价之间的差价由政府承担.王宏按照相关政策投资销售本市生产的一种新型节能灯,已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=-10x+400.‎ ‎(1)王宏在开始创业的第一个月将销售单价定为18元,那么政府这个月为他承担的总差价为多少元?‎ ‎(2)设王宏获得的利润为w(元),当销售单价为多少元时,每月可获得最大利润?‎ ‎(3)若物价部门规定,这种节能灯销售单价不得高于24元.如果王宏想要每月获得的利润不低于2000元,那么政府为他承担的总差价最少为多少元?‎ 10‎ ‎【参考答案】‎ ‎17.解:(1)原式=‎1‎‎2‎-2×‎3‎‎2‎+2‎3‎+1=‎3‎‎2‎‎+‎‎3‎.‎ ‎(2)a‎2‎‎-2a+1‎a‎2‎‎-4‎÷a-1‎a-2‎‎+‎1‎a+2‎=‎‎(a-1‎‎)‎‎2‎‎(a+2)(a-2)‎·a-2‎a-1‎‎+‎1‎a+2‎=a-1‎a+2‎+‎1‎a+2‎=‎aa+2‎,‎ 当a=|1-‎3‎|-tan60°+‎1‎‎2‎-1=‎3‎-1-‎3‎+2=1时,原式=‎1‎‎1+2‎‎=‎‎1‎‎3‎.‎ ‎18.解:(1)200　[解析]∵喜欢A项目的有20人,所占扇形的圆心角为36°,‎ ‎∴这次被调查的学生共有20÷‎36‎‎360‎=200(人).‎ 故答案为200.‎ ‎(2)C项目对应人数为200-20-80-40=60(人),‎ 补图如下:‎ ‎(3)画树状图如下.‎ ‎∵共有12种等可能的情况,恰好选中甲、乙两位同学有2种情况,‎ ‎∴P(恰好选中甲、乙)=‎2‎‎12‎‎=‎‎1‎‎6‎.‎ ‎19.解:(1)如图,过点F作FN⊥KD于点N,过点E作EM⊥FN于点M.‎ ‎∵EF+FG=166,FG=100,∴EF=66.‎ ‎∵∠FGK=80°,‎ ‎∴FN=100sin80°≈98.‎ 又∵∠EFG=125°,∴∠EFM=180°-125°-10°=45°.‎ 10‎ ‎∴FM=66cos45°=33‎2‎≈46.53.‎ ‎∴MN=FN+FM≈144.5.‎ ‎∴他头部E点与地面DK相距约144.5 cm.‎ ‎(2)如图,过点E作EP⊥AB于点P,延长OB,交MN于点H.‎ ‎∵AB=48,O为AB的中点,∴AO=BO=24.‎ ‎∵EM=66sin45°≈46.53,∴PH≈46.53,‎ ‎∵GN=100cos80°≈17,CG=15,‎ ‎∴OH=24+15+17=56,‎ OP=OH-PH=56-46.53=9.47≈9.5.‎ ‎∴他应前进9.5 cm.‎ ‎20.解:(1)证明:∵四边形ABCD是平行四边形,‎ ‎∴AB=CD,∠BAE=∠DCF.‎ 在△ABE和△CDF中,‎ AB=CD,‎‎∠BAE=∠DCF,‎AE=CF,‎ ‎∴△ABE≌△CDF.‎ ‎(2)四边形BEDF是菱形.‎ 理由如下:‎ ‎∵四边形ABCD是平行四边形,‎ ‎∴AD∥BC,AD=BC.‎ ‎∵AE=CF,∴DE=BF.‎ ‎∴四边形BEDF是平行四边形.‎ ‎∴OB=OD.‎ ‎∵DG=BG,‎ ‎∴EF⊥BD.‎ ‎∴四边形BEDF是菱形.‎ ‎21.解:(1)证明:连接CD.‎ 10‎ ‎∵AC是☉O的直径,‎ ‎∴∠ADC=90°,‎ ‎∴∠DAC+∠ACD=90°.‎ ‎∵BC是☉O的切线,‎ ‎∴∠ACB=90°,‎ ‎∴∠DAC+∠ABC=90°,‎ ‎∴∠ABC=∠ACD.‎ ‎∵∠AED=∠ACD,‎ ‎∴∠ABC=∠AED.‎ ‎(2)∵∠AED=∠ACD=∠ABC,‎ ‎∴tan∠ACD=tan∠AED=tan∠ABC=‎4‎‎3‎,‎ ‎∴tan∠ACD=ADCD‎=‎‎4‎‎3‎,‎ 即‎32‎‎5‎CD‎=‎‎4‎‎3‎,∴CD=‎24‎‎5‎.∴AC=8.‎ ‎∵AF=6,∴FC=2,‎ ‎∵tan∠ABC=ACBC‎=‎‎4‎‎3‎,即‎8‎BC‎=‎‎4‎‎3‎,‎ ‎∴BC=6,∴BF=2‎10‎.‎ ‎22.解:(1)当x=18时,y=-10x+400=-10×18+400=220,‎ ‎220×(12-10)=220×2=440(元).‎ 故政府这个月为他承担的总差价为440元.‎ ‎(2)依题意,得w=(x-10)(-10x+400)‎ ‎=-10x2+500x-4000‎ ‎=-10(x-25)2+2250.‎ ‎∵a=-10<0,‎ ‎∴当x=25时,w有最大值,为2250.‎ 故当销售单价定为25元时,每月可获得最大利润2250元.‎ ‎(3)令-10x2+500x-4000=2000,‎ 解得x1=20,x2=30.‎ ‎∵a=-10<0,抛物线的开口向下,‎ ‎∴当20≤x≤30时,2000≤w≤2250.‎ 10‎ 又∵x≤24,‎ ‎∴当20≤x≤24时,w≥2000.‎ ‎∵y=-10x+400中,-10<0,‎ ‎∴当x=24时,y最小,政府每个月为他承担的总差价最少,y=-10×24+400=160,‎ ‎160×(12-10)=320(元).‎ 故销售单价定为24元时,政府每个月为他承担的总差价最少,为320元.‎ 10‎