2018年浙江省杭州市中考数学试题含答案 8页

‎2018年杭州市中考数学试题 一、选择题（本题有10小题，每小题3分，共30分）‎ ‎1. =（ ）‎ A. 3 B. C. D. ‎ ‎2.数据1800000用科学计数法表示为（ ）‎ A. B. C. D. ‎ ‎3.下列计算正确的是（ ）‎ A. B. C. D. ‎ ‎4.测试五位学生“一分钟跳绳”成绩，得到五个各不相同的数据，统计时，出现了一处错误：将最高成绩写得更高了。计算结果不受影响的是（ ）‎ A.方差 B. 标准差 C. 中位数 D. 平均数 ‎ ‎5.若线段 AM，AN分别是边上的高线和中线，则（ ）‎ A. B. C. D. ‎ ‎6.某次知识竞赛共有20道题，规定：每答对一题得+5分，每答错一题得-2分，不答的题得0分。已知圆圆这次竞赛得了60分，设圆圆答对了道题，答错了道题，则（ ）‎ A. B. C. D. ‎ ‎7.一个两位数，它的十位数字是3，个位数字是抛掷一枚质地均匀的骰子（六个面分别有数字1~6）朝上一面的数字。任意抛掷这枚骰子一次，得到的两位数是3的倍数的概率等于（ ）‎ A. B. C. D. ‎ ‎8.如图，已知点P矩形ABCD内一点（不含边界），设，，，，若,则（ ）‎ A. B. ‎ ‎ C. D. ‎ ‎9.四位同学在研究函数时，甲发现当时，函数有最小值；乙发现是方程的一个根；丙发现函数的最小值为3；丁发现当时，.已知这四位同学中只有一位发现的结论是错误的，则该同学是（ ）‎ A. 甲 B.乙 C. 丙 D.丁 ‎ ‎10.如图，在中，点D在AB边上，，与边交于点E，连结BE，记的面积分别为，（ ）‎ 8‎ A. 若，则 B. 若，则 ‎ C. 若，则 D. 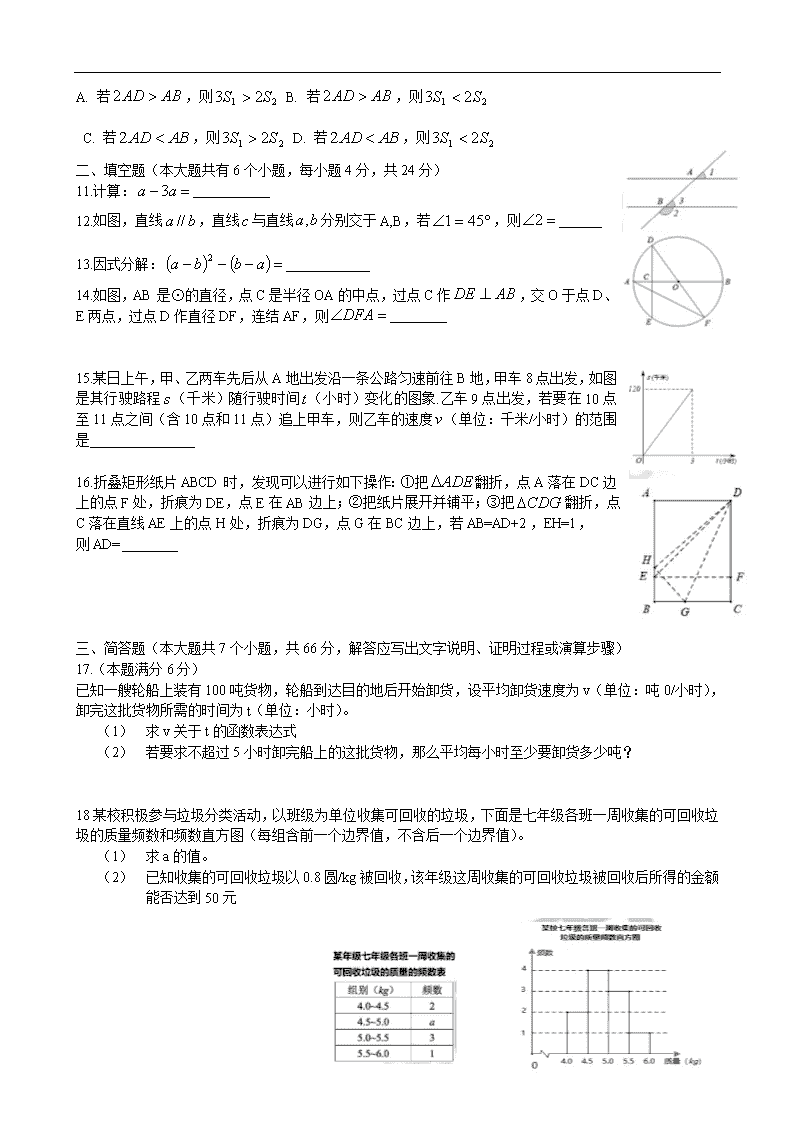若，则 ‎ 二、填空题（本大题共有6个小题，每小题4分，共24分）‎ ‎11.计算： ‎ ‎12.如图，直线，直线与直线分别交于A,B，若，则 ‎ ‎13.因式分解： ‎ ‎14.如图，AB是⊙的直径，点C是半径OA的中点，过点C作，交O于点D、E两点，过点D作直径DF，连结AF，则 ‎ ‎15.某日上午，甲、乙两车先后从A地出发沿一条公路匀速前往B地，甲车8点出发，如图是其行驶路程（千米）随行驶时间（小时）变化的图象.乙车9点出发，若要在10点至11点之间（含10点和11点）追上甲车，则乙车的速度（单位：千米/小时）的范围是 ‎ ‎16.折叠矩形纸片ABCD时，发现可以进行如下操作：①把翻折，点A落在DC边上的点F处，折痕为DE，点E在AB边上；②把纸片展开并铺平；③把翻折，点C落在直线AE上的点H处，折痕为DG，点G在BC边上，若AB=AD+2，EH=1，‎ 则AD= ‎ 三、简答题（本大题共7个小题，共66分，解答应写出文字说明、证明过程或演算步骤）‎ ‎17.（本题满分6分）‎ 已知一艘轮船上装有100吨货物，轮船到达目的地后开始卸货，设平均卸货速度为v（单位：吨0/小时），卸完这批货物所需的时间为t（单位：小时）。‎ （1） 求v关于t的函数表达式 （2） 若要求不超过5小时卸完船上的这批货物，那么平均每小时至少要卸货多少吨？‎ ‎18某校积极参与垃圾分类活动，以班级为单位收集可回收的垃圾，下面是七年级各班一周收集的可回收垃圾的质量频数和频数直方图（每组含前一个边界值，不含后一个边界值）。‎ （1） 求a的值。‎ （2） 已知收集的可回收垃圾以0.8圆/kg被回收，该年级这周收集的可回收垃圾被回收后所得的金额能否达到50元 8‎ ‎19.（本题满分8分）‎ 如图，在中，AB=AC，AD为BC边上的中线DE⊥AB于点E ‎（1）求证：∽‎ ‎（2）若AB=13，BC=10，求线段DE的长 ‎20.（本题满分10分）‎ 设一次函数（是常数，）的图象过A（1,3），B（-1，-1）‎ ‎（1）求该一次函数的表达式；‎ ‎（2）若点在该一次函数图象上，求的值；‎ ‎（3）已知点C，D在该一次函数图象上，设，判断反比例函数的图象所在的象限，说明理由。‎ ‎21.（本题满分10分）‎ 如图，在中，，以点B为圆心，BC的长为半径画弧，交线段AB于点D,以点A为圆心，AD长为半径画弧，交线段AC于点E，连结CD ‎（1）若，求的度数；‎ ‎（2）设 ‎①线段AD的长度是方程的一个根吗？说明理由。‎ ‎②若线段AD=EC，求的值. ‎ ‎22.（本题满分12分）‎ 设二次函数（是常数，）‎ ‎（1）判断该二次函数图象与x轴交点的个数，说明理由.‎ ‎（2）若该二次函数的图象经过A（-1,4），B（0，-1），C（1,1）三个点中的其中两个点，求该二次函数的表达式；‎ ‎（3）若，点P（2，m）(m>0)在该二次函数图象上，求证：.‎ 8‎ ‎23.如图，在正方形ABCD中，点G在边BC上（不与点B、C重合），连接AG，作DE⊥AG,于点E，BF⊥AG于点F，设 ‎（1）求证：AE=BF ‎（2）连接BE、DF，设，求证：‎ ‎（3）设线段AG与对角线BD交于点H， 和四边形CDHG的面积分别为 ‎，求的最大值.‎ 8‎ 参考答案：‎ ‎1.A 2.B 3.A 4.C 5.D 6.C 7.B 8.A 9.B 10.D ‎11.‎ ‎12. 135度 ‎13.‎ ‎14.30度 ‎15.‎ ‎16.‎ ‎17.解：（1）（）‎ ‎（2）‎ 当时 当时，‎ ‎∴‎ ‎∴平均每小时至少要卸货20吨 ‎18. ‎ ‎19. ‎ 8‎ 8‎ 8‎ 8‎