2018年广州中考数学试题含答案 6页

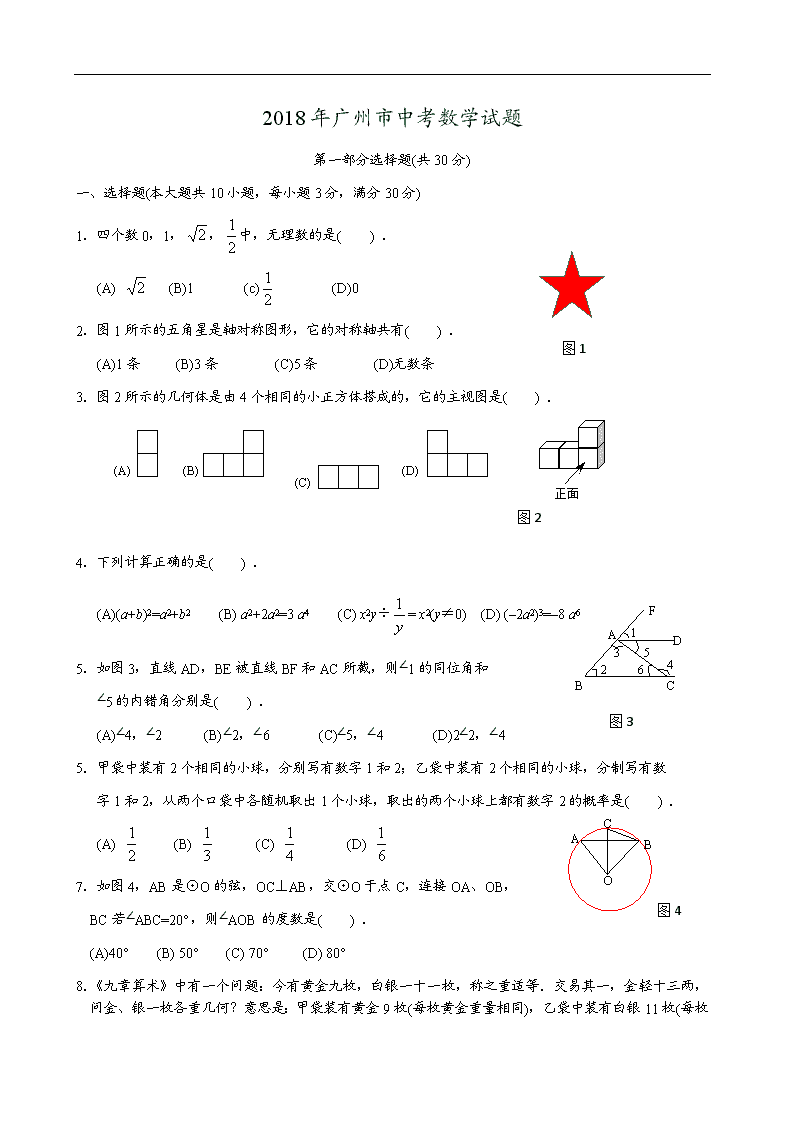
‎2018年广州市中考数学试题 第一部分选择题(共30分)‎ 一、选择题(本大题共10小题，每小题3分，满分30分)‎ ‎1．四个数0，1，，中，无理数的是( ) ．‎ ‎(A) (B)1 (c) (D)0‎ 图1‎ ‎2．图1所示的五角星是轴对称图形，它的对称轴共有( ) ．‎ ‎ (A)1条 (B)3条 (C)5条 (D)无数条 ‎3．图2所示的几何体是由4个相同的小正方体搭成的，它的主视图是( ) ．‎ ‎(D)‎ ‎(B)‎ ‎(A)‎ 正面 ‎(C)‎ 图2‎ ‎4．下列计算正确的是( ) ．‎ A D F C B ‎2‎ ‎3‎ ‎1‎ ‎5‎ ‎4‎ ‎6‎ ‎ (A)(a+b)2=a2+b2 (B) a2+2a2=3 a4 (C) x2y÷= x2(y≠0) (D) (–2a2)3=–8 a6‎ ‎5．如图3，直线AD，BE被直线BF和AC所截，则∠1的同位角和 图3‎ ‎∠5的内错角分别是( ) ．‎ ‎(A)∠4，∠2 (B)∠2，∠6 (C)∠5，∠4 (D)2∠2，∠4‎ ‎5．甲袋中装有2个相同的小球，分别写有数字1和2；乙袋中装有2个相同的小球，分制写有数 A B C O 字1和2，从两个口袋中各随机取出1个小球，取出的两个小球上都有数字2的概率是( ) ．‎ ‎ (A) (B) (C) (D) ‎ 图4‎ ‎7．如图4，AB是⊙O的弦，OC⊥AB，交⊙O于点C，连接OA、OB，‎ BC若∠ABC=20°，则∠AOB的度数是( ) ．‎ ‎(A)40° (B) 50° (C) 70° (D) 80°‎ ‎8．《九章算术》中有一个问题：今有黄金九枚，白银一十一枚，称之重适等．交易其一，金轻十三两，问金、银一枚各重几何？意 思是：甲袋装有黄金9枚(每枚黄金重量相同)，乙袋中装有白银11枚(每枚白银重量相同)，称重两袋相等．两袋互相交换1枚后，甲袋比乙袋轻了13两(袋子重量忽略不计)，黄金、白银每枚各重多少两?设每枚黄金重x两，每枚白银重y两，据题意得：( ) ．‎ ‎(A) (B) ‎ ‎ (C) (D) ‎ ‎9．一次函数y=ax+b和反比例函数y=在同一直角坐标系中的大致图象是( ) ．‎ O x y ‎1‎ A1‎ A2‎ A3‎ A4‎ A5‎ A6‎ A7‎ A8‎ A9‎ A10‎ A11‎ A12‎ ‎10．在平面直角坐标系中，一个智能机器人接到如下指令：从原点O出发，按向右，向上，向右，向下的方向依次不断移动，每次移动1m，其行走路线如图5所示，第1次移动到A1，第2次移动到A2，…，第次移动到An，则△OA2A2018的面积是( m2) ．‎ ‎1‎ ‎(A)504 (B) (C) (D)1009‎ 第二部分非选择题(共120分)‎ 图5‎ 二、填空题(本大题共6小题，每小题3分，满分18分)‎ 图6‎ C B A ‎11．已知二次函数y=x2，当x>0时，y随x的增大而______．(填“增大”或“减小”)‎ ‎12．如图6，杆高AB=8m，某一时制，旗杆影子长BC=16m，则tanC=______．‎ ‎13．方程的解是_______．‎ E B D A C O 哦O x 哦O y 哦O A D C B 图7‎ C ‎14．如图7，若菱形ABCD的顶点A，B的坐标分别为(3，0 )（–2，0），‎ 点D在y轴上，则点C的坐标是_______．‎ ‎15．如图8，数轴上点A表示的数为a，化简：=_______．‎ ‎16．如图9，CE是□ABCD接力赛AB的垂直平分线，垂足为O，‎ CE与DA的延长线交于点E，连接AC、BE、DO，DO与 A ‎0 a 2‎ 图8‎ AC交于点F、则下列结论：‎ ‎①四边形ACBE是菱形；②∠ACD=∠BAE；‎ ‎③AF:BE=2:3 ④S四边形AFOE：S△CDO=2:3 ‎ C B E A D F O 其中正确的结论有_______．（填写所有正确结论的序号）‎ 三，解答题(共102分)‎ ‎17．(9分)解不等式组: ‎ 图10‎ 图9‎ ‎18．(9分)如图10，AB与CD相交于点E， AE=CE， DE=BE ‎ 求证：∠A=∠C ‎19．(10分)已知 ‎ (1)化简T：‎ ‎(2)若正方形ABCD的边长为a，且它的面积为9，求T的值．‎ ‎20．(10分)随着移动互联网的快速发展，基于互联网的共享单车应运而生，为了解小区居民使用共享单车的情况，某研究小组随机采访该小区的10位居民，得到这10位居民一周内使用共享单车的次数分别为：17，12，15，20，17，0，7，26，17，9‎ ‎(1)这组数据的中位数是_______，众数是________；‎ ‎(2)计算这10位居民一周内使用共享单车的平均次数；‎ ‎(3)若该小区有200名居民，试估计该小区居民一周内使用共享单车的总次数 ‎21．(12分)友谊商店A型号笔记本电脑的售价是a元/台．最近，该商店对A型号笔记本电脑举行促销活动，有两种优惠方案，方案一：每台按售价的九折销售；方案二：若购买不超过5台，每台按售价销售；若超过5台，超过的部分每台按售价的八折销售．某公司一次性从友谊商店购买A型号笔记本电脑x台．‎ ‎(1)当x=8时，应选择哪种方案，该公购买费用最少?最少费用是多少元?‎ ‎(2)若该公司采用方案二购买更合算，求x的取值范围．‎ ‎22．(12分)设P(x，0)是x轴上的一个动点，它与原点的距离为y1．‎ ‎(1)求 y1关于x的函数解析式，并画出这个函数的图象；‎ ‎(2)若反比例函数y2=的图象与函数y1的图象相交于点A，且点A的纵坐标为2．‎ ‎①求k的值；‎ ‎②结合图象，当y1> y2时，写x出的取值范围．‎ 图11‎ C B A D ‎23．(12分)如图11，在四边形ABCD中，∠B=∠C=，AB>CD，AD=AB+CD． ‎ ‎ (1)利用尺规作∠ADC的平分线DE，交BC于点E，‎ 连接AE(保留作图痕迹，不写作法)；‎ ‎(2)在(1)的条件下 ‎①证明:AE⊥DE；‎ ‎②若CD=2，AB=4，点M，N分别是AE，AB上的动点，‎ 求BM+ACN的最小值 ‎24．(14分)已知抛物线y=x2+mx–2m–4(m>0) ．‎ ‎(1)证明：该抛物线与x轴总有两个不同的交点；‎ ‎(2)设该抛物线与x轴的两个交点分别为A、B(点A在点B的右侧)，与y轴交于C点，A、B、C三点都在⊙P上．‎ ‎①试判断：不论m取任何正数，⊙P是否经过y轴上某个定点?若是，求出该定点的坐标；若不是，说明理由 ‎②若点C关于直线x=–的对称点为点E，点D(0，1)，述接BE、BD、DE，△BDE的周长记为l，⊙P的半径记为r，求的值．‎ ‎25．(14分)如图12，在四边形ABCD中，∠B=60°，∠D=30°，AB=BC ‎(1)求∠A+∠C的度数；‎ ‎(2)连接BD，探究AD，BD，CD三者之间的数量关系，说明理由；‎ ‎(3)若AB=1，点E在四边形ABCD内部运动，且满足AE2=BE2+CE2，求点E运动路径的长度．‎ C B A D 图12‎