2020年辽宁省铁岭市中考数学试卷【含答案】 9页

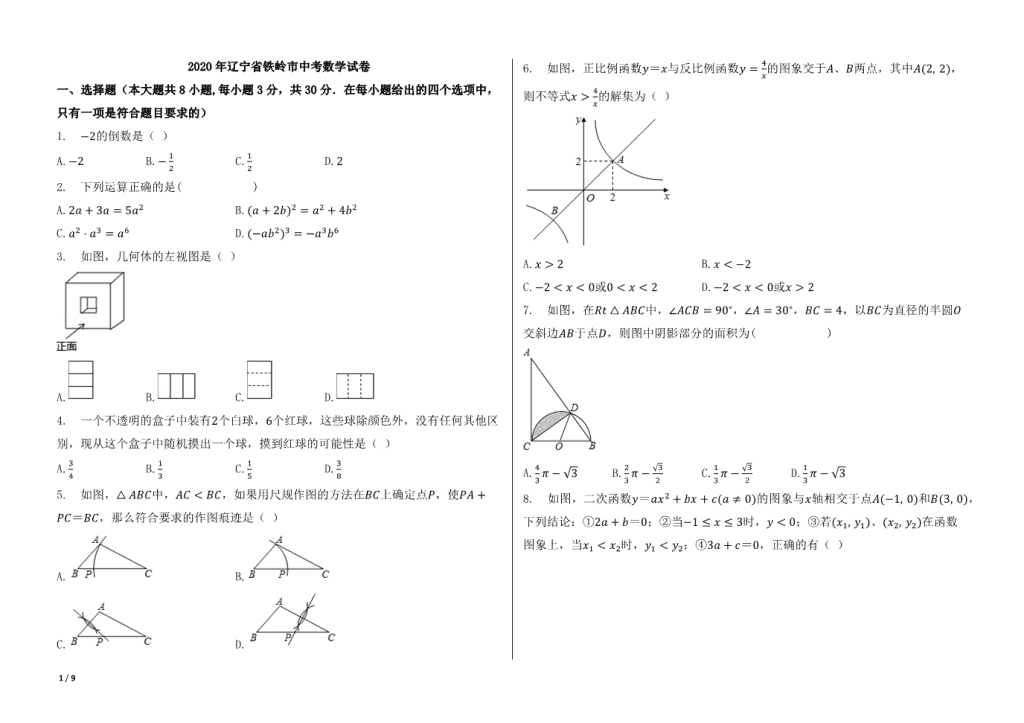
1 / 9 2020 年辽宁省铁岭市中考数学试卷 一、选择题（本大题共 8 小题,每小题 3 分，共 30 分．在每小题给出的四个选项中， 只有一项是符合题目要求的） 1. −2的倒数是（ ） A.−2 B.− 1 2 C.1 2 D.2 2. 下列运算正确的是( ) A.2푎 + 3푎 = 5푎2 B.(푎 + 2푏)2 = 푎2 + 4푏2 C.푎2 ⋅ 푎3 = 푎6 D.(−푎푏2)3 = −푎3푏6 3. 如图，几何体的左视图是（ ） A. B. C. D. 4. 一个不透明的盒子中装有2个白球，6个红球，这些球除颜色外，没有任何其他区 别，现从这个盒子中随机摸出一个球，摸到红球的可能性是（ ） A.3 4 B.1 3 C.1 5 D.3 8 5. 如图，△ 퐴퐵퐶中，퐴퐶 < 퐵퐶，如果用尺规作图的方法在퐵퐶上确定点푃，使푃퐴 + 푃퐶＝퐵퐶，那么符合要求的作图痕迹是（ ） A. B. C. D. 6. 如图，正比例函数푦＝푥与反比例函数푦 = 4 푥 的图象交于퐴、퐵两点，其中퐴(2,  2)， 则不等式푥 > 4 푥 的解集为（ ） A.푥 > 2 B.푥 < −2 C.−2 < 푥 < 0或0 < 푥 < 2 D.−2 < 푥 < 0或푥 > 2 7. 如图，在푅푡 △ 퐴퐵퐶中，∠퐴퐶퐵 = 90∘，∠퐴 = 30∘，퐵퐶 = 4，以퐵퐶为直径的半圆푂 交斜边퐴퐵于点퐷，则图中阴影部分的面积为( ) A.4 3 휋 − √3 B.2 3 휋 − √3 2 C.1 3 휋 − √3 2 D.1 3 휋 − √3 8. 如图，二次函数푦＝푎푥2 + 푏푥 + 푐(푎 ≠ 0)的图象与푥轴相交于点퐴(−1,  0)和퐵(3,  0)， 下列结论：①2푎 + 푏＝0；②当−1 ≤ 푥 ≤ 3时，푦 < 0；③若(푥1, 푦1)、(푥2, 푦2)在函数 图象上，当푥1 < 푥2时，푦1 < 푦2；④3푎 + 푐＝0，正确的有（ ） 2 / 9 A.①②④ B.①④ C.①②③ D.①③④ 二、填空题（本大题共 6 小题，每小题 3 分，共 18 分） 9. 我国首艘国产航母排水量约为65000吨，将65000用科学记数法记为________． 10. 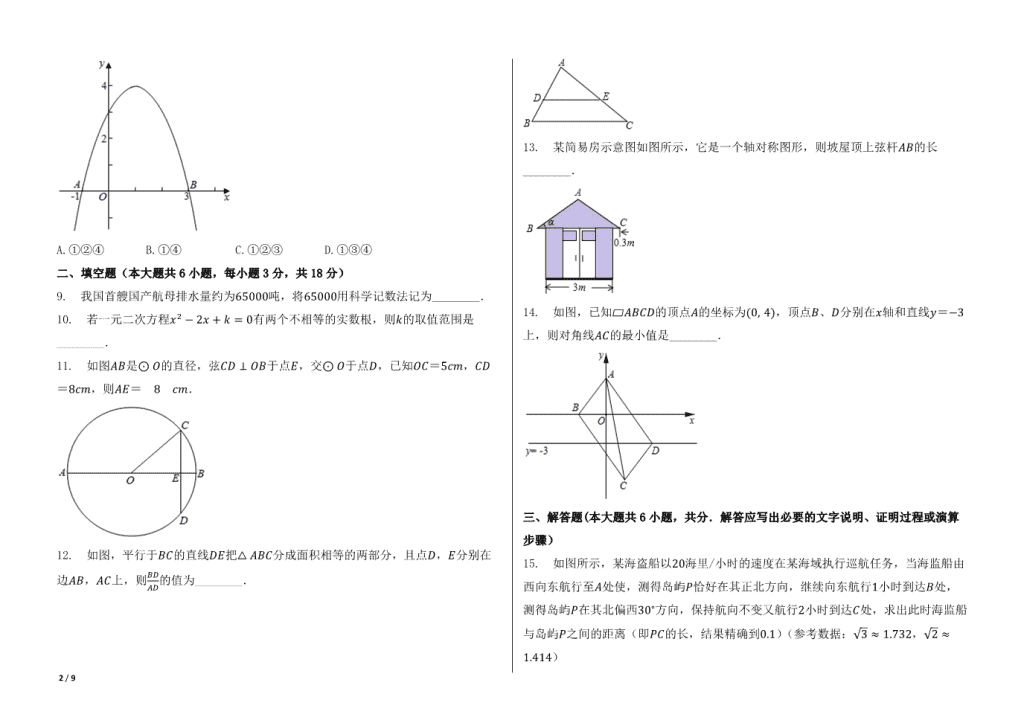若一元二次方程푥2 − 2푥 + 푘 = 0有两个不相等的实数根，则푘的取值范围是 ________． 11. 如图퐴퐵是⊙ 푂的直径，弦퐶퐷 ⊥ 푂퐵于点퐸，交⊙ 푂于点퐷，已知푂퐶＝5푐푚，퐶퐷 ＝8푐푚，则퐴퐸＝ 8 푐푚． 12. 如图，平行于퐵퐶的直线퐷퐸把△ 퐴퐵퐶分成面积相等的两部分，且点퐷，퐸分别在 边퐴퐵，퐴퐶上，则퐵퐷 퐴퐷 的值为________． 13. 某简易房示意图如图所示，它是一个轴对称图形，则坡屋顶上弦杆퐴퐵的长 ________． 14. 如图，已知▱퐴퐵퐶퐷的顶点퐴的坐标为(0,  4)，顶点퐵、퐷分别在푥轴和直线푦＝−3 上，则对角线퐴퐶的最小值是________． 三、解答题(本大题共 6 小题，共分．解答应写出必要的文字说明、证明过程或演算 步骤） 15. 如图所示，某海盗船以20海里/小时的速度在某海域执行巡航任务，当海监船由 西向东航行至퐴处使，测得岛屿푃恰好在其正北方向，继续向东航行1小时到达퐵处， 测得岛屿푃在其北偏西30∘方向，保持航向不变又航行2小时到达퐶处，求出此时海监船 与岛屿푃之间的距离（即푃퐶的长，结果精确到0.1）（参考数据：√3 ≈ 1.732，√2 ≈ 1.414） 3 / 9 16. 如图，某反比例函数图象的一支经过点퐴(2,  3)和点퐵（点퐵在点퐴的右侧）作 퐵퐶 ⊥ 푦轴于点퐶，连结퐴퐵，퐴퐶．若△ 퐴퐵퐶的面积为6，求点퐵的坐标． 17. 某企业设计了一款工艺品，每件的成本是50元，为了合理定价，投放市场进行试 销．据市场调查，销售单价是100元时，每天的销售量是50件，而销售单价每降低1元， 每天就可多售出5件，但要求销售单价不得低于成本. (1)求每天的销售利润푦（元）与销售单价푥（元）之间的函数关系式； (2)求出销售单价为多少元时，每天的销售利润最大？最大利润是多少？ 4 / 9 18. 如图，在푅푡 △ 퐴퐵퐶中，∠퐴퐶퐵＝90∘，∠퐵＝60∘，퐷为퐴퐵边的中点，连接퐷퐶过퐷作 퐷퐸 ⊥ 퐷퐶交퐴퐶于点퐸． （1）求∠퐸퐷퐴的度数； （2）如图2，퐹为퐵퐶边上一点，连接퐷퐹，过퐷作퐷퐺 ⊥ 퐷퐹交퐴퐶于点퐺，请判断线段퐶퐹 与퐸퐺的数量关系，并说明理由． 19. 如图，퐴퐵是⊙ 푂的直径，点퐶为⊙ 푂上一点，퐶푁为⊙ 푂的切线，푂푀 ⊥ 퐴퐵于点푂， 分别交퐴퐶，퐶푁于퐷，푀两点． (1)求证：푀퐷 = 푀퐶； (2)若⊙ 푂的半径为5，퐴퐶 = 4√5，求푀퐶的长． 5 / 9 20. 如图，抛物线푦＝푎푥2 + 푏푥 + 푐经过퐴(−1,  0)、퐵(3,  0)、퐶(0,  3)三点，对称轴与抛 物线相交于点푃、与퐵퐶相交于点퐸，与푥轴交于点퐻，连接푃퐵． （1）求该抛物线的解析式； （2）抛物线上存在一点퐺，使∠퐺퐵퐴 + ∠푃퐵퐸＝45∘，请求出点퐺的坐标； （3）抛物线上是否存在一点푄，使△ 푄퐸퐵与△ 푃퐸퐵的面积相等，若存在，请直接写出 点푄的坐标；若不存在，说明理由． 6 / 9 参考答案与试题解析 2020 年辽宁省铁岭市中考数学试卷 一、选择题（本大题共 8 小题,每小题 3 分，共 30 分．在每小题给出的四个选项中， 只有一项是符合题目要求的） 1.B 2.D 3.C 4.A 5.C 6.D 7.A 8.B 二、填空题（本大题共 6 小题，每小题 3 分，共 18 分） 9.6.5 × 104 10.푘 < 1 11.8 12.√2 − 1 13. 9 5cos훼 푚 14.11 三、解答题(本大题共 6 小题，共分．解答应写出必要的文字说明、证明过程或演算 步骤） 15.在푅푡 △ 푃퐴퐵中，∵ ∠퐴푃퐵＝30∘， ∴ 푃퐵＝2퐴퐵， 由题意퐵퐶＝2퐴퐵， ∴ 푃퐵＝퐵퐶， ∴ ∠퐶＝∠퐶푃퐵， ∵ ∠퐴퐵푃＝∠퐶 + ∠퐶푃퐵＝60∘， ∴ ∠퐶＝30∘， ∴ 푃퐶＝2푃퐴， ∵ 푃퐴＝퐴퐵 ⋅ tan60∘， ∴ 푃퐶＝2 × 20 × √3 ≈ 69.3（海里）． 16.由题意得，푘＝푥푦＝2 × 3＝6 ∴ 反比例函数的解析式为：푦 = 6 푥 ． 设퐵点坐标为(푎,  푏)，如图， 作퐴퐷 ⊥ 퐵퐶于퐷，则퐷(2,  푏)， ∵ 反比例函数푦 = 6 푥 的图象经过点퐵(푎,  푏) ∴ 푏 = 6 푎 ， ∴ 퐴퐷＝3 − 6 푎 ． ∴ 푆△퐴퐵퐶 = 1 2 퐵퐶 ⋅ 퐴퐷 = 1 2 푎(3 − 6 푎)＝6， 解得푎＝6， ∴ 푏 = 6 푎 = 1 ∴ 퐵(6,  1)． 17.解：(1)푦 = (푥 − 50)[50 + 5(100 − 푥)] = (푥 − 50)(−5푥 + 550) = −5푥2 + 800푥 − 27500, 7 / 9 所以푦 = −5푥2 + 800푥 − 27500(50 ≤ 푥 ≤ 100)； (2)푦 = −5푥2 + 800푥 − 27500 = −5(푥 − 80)2 + 4500, ∵ 푎 = −5 < 0， ∴ 抛物线开口向下． ∵ 50 ≤ 푥 ≤ 100，对称轴是直线푥 = 80， ∴ 当푥 = 80时，푦最大值 = 4500； 即销售单价为80元时，每天的销售利润最大，最大利润是4500元． 18.如图1，在푅푡 △ 퐴퐵퐶中，∠퐴퐶퐵＝90∘，∠퐵＝60∘， ∴ ∠퐴＝30∘， ∵ 퐷为퐴퐵边的中点， ∴ 퐶퐷＝퐵퐷＝퐴퐷， ∴ △ 퐵퐶퐷是等边三角形，∠퐴퐶퐷＝∠퐴＝30∘， ∵ ∠퐶퐷퐸＝90∘， ∴ ∠퐶퐸퐷＝60∘， ∴ ∠퐸퐷퐴＝30∘； 如图2，在푅푡 △ 퐶퐷퐸中，∠퐴퐶퐷＝30∘， ∴ tan30∘ = 퐷퐸 퐶퐷 ， ∴ 퐷퐸 퐶퐷 = √3 3 ， ∵ ∠퐹퐷퐺＝∠퐶퐷퐸＝90∘， ∴ ∠퐹퐷퐶＝∠퐺퐷퐸， ∴ ∠퐹퐶퐷＝∠퐺퐸퐷＝60∘， ∴ △ 퐹퐶퐷 ∽ 퐺퐸퐷， ∴ 퐺퐸 퐹퐶 = 퐷퐸 퐶퐷 = √3 3 ， ∴ 퐹퐶 = √3퐺퐸． 19.解：(1)连接푂퐶. ∵ 퐶푁为⊙ 푂的切线， ∴ 푂퐶 ⊥ 퐶푀，∠푂퐶퐴 + ∠퐴퐶푀 = 90∘. ∵ 푂푀 ⊥ 퐴퐵， ∴ ∠푂퐴퐶 + ∠푂퐷퐴 = 90∘. ∵ 푂퐴 = 푂퐶， ∴ ∠푂퐴퐶 = ∠푂퐶퐴， ∴ ∠퐴퐶푀 = ∠푂퐷퐴 = ∠퐶퐷푀， ∴ 푀퐷 = 푀퐶； 8 / 9 (2)由题意可知퐴퐵 = 5 × 2 = 10，퐴퐶 = 4√5. ∵ 퐴퐵是⊙ 푂的直径， ∴ ∠퐴퐶퐵 = 90∘， ∴ 퐵퐶 = √102 − (4√5)2 = 2√5. ∵ ∠퐴푂퐷 = ∠퐴퐶퐵，∠퐴 = ∠퐴， ∴ △ 퐴푂퐷 ∼△ 퐴퐶퐵， ∴ 푂퐷 퐶퐵 = 퐴푂 퐴퐶 ，即 푂퐷 2√5 = 5 4√5 ， 可得：푂퐷 = 2.5. 设푀퐶 = 푀퐷 = 푥. 在푅푡 △ 푂퐶푀中，由勾股定理得：(푥 + 2.5)2 = 푥2 + 52， 解得：푥 = 15 4 ，即푀퐶 = 15 4 ． 20.把퐴(−1,  0)，퐵(3,  0)，퐶(0,  3)三点代入抛物线解析式 { 푎 − 푏 + 푐 = 0 9푎 + 3푏 + 푐 = 0 푐 = 3 ， 解得：{ 푎 = −1 푏 = 2 푐 = 3 ， ∴ 该抛物线的解析式为푦＝−푥2 + 2푥 + 3； 由푦＝−푥2 + 2푥 + 3＝−(푥 − 1)2 + 4， 则顶点푃(1,  4)，对称轴为直线푥＝1， ∴ 퐻(1,  0)， ∴ 푃퐻＝4，퐵퐻＝2， ∵ 퐵(3,  0)，퐶(0,  3)， ∴ 直线퐵퐶解析式为푦＝−푥 + 3， ∴ 点퐸(1,  2)， ∵ 퐵(3,  0)，퐶(0,  3)， ∴ 푂퐵＝푂퐶， ∴ ∠퐶퐵푂＝45∘， 若点퐺在直线퐴퐵的上方时， ∵ 푃퐻 ⊥ 퐴퐵，∠퐶퐵푂＝45∘， ∴ ∠퐻퐸퐵＝45∘， ∴ ∠푃퐵퐸 + ∠퐵푃퐸＝45∘， ∵ ∠퐺퐵퐴 + ∠푃퐵퐸＝45∘， ∴ ∠퐵푃퐸＝∠퐺퐵퐴， ∴ tan∠퐵푃퐻＝tan∠퐺퐵퐴 = 퐵퐻 푃퐻 = 푂퐹 푂퐵 ， ∴ 2 4 = 푂퐹 3 ， ∴ 푂퐹 = 3 2 ， ∴ 点퐹(0, 3 2)， ∴ 直线퐵퐹解析式为：푦 = − 1 2 푥 + 3 2 ， 联立方程组可得：{ 푦 = − 1 2 푥 + 3 2 푦 = −푥2 + 2푥 + 3 ， 解得：{푥1 = 3 푦1 = 0 或{ 푥2 = − 1 2 푦2 = 7 4 ， 9 / 9 ∴ 点퐺的坐标为(− 1 2 , 7 4)； 若点퐺在直线퐴퐵的下方时， 由对称性可得：点퐹′(0, − 3 2)， ∴ 直线퐵퐹解析式为：푦 = 1 2 푥 − 3 2 ， 联立方程组可得：{ 푦 = 1 2 푥 − 3 2 푦 = −푥2 + 2푥 + 3 ， 解得：{ 푥1 = − 3 2 푦1 = − 9 4 或{푥2 = 3 푦2 = 0 ， ∴ 点퐺′的坐标为(− 3 2 , − 9 4)， 综上所述：点퐺的坐标为(− 1 2 , 7 4)或(− 3 2 , − 9 4)； 存在， ∵ 点퐸(1,  2)，顶点푃(1,  4)， ∴ 푃퐸＝2，푃퐻＝4， ∴ 퐸퐻＝2＝푃퐸， 如图2，过点푃作푃푄 // 퐵퐶，交抛物线于푄，此时△ 푄퐸퐵与△ 푃퐸퐵的面积相等， ∵ 푃푁 // 퐵퐶，点푃坐标(1,  4)，直线퐵퐶解析式为푦＝−푥 + 3， ∴ 푃푄解析式为푦＝−푥 + 5， 联立方程组得：{ 푦 = −푥 + 5 푦 = −푥2 + 2푥 + 3 ， 解得：{푥1 = 1 푦1 = 4 或{푥2 = 2 푦2 = 3 ， ∴ 点푄(2,  3)， 过点퐻作퐻푄′ // 퐵퐶，交抛物线于푄′、푄′′ ， ∴ 푃푄 // 퐵퐶 // 퐻푄′， ∵ 푃퐸＝퐸퐻， ∴ 푃푄与퐵퐶之间的距离＝퐵퐶与퐻푄′之间的距离， ∴ △ 푄퐸퐵与△ 푃퐸퐵的面积相等， ∵ 푃푄 // 퐵퐶，点퐻(1,  0)，直线퐵퐶解析式为푦＝−푥 + 3， ∴ 直线푄′퐻的解析式为：푦＝−푥 + 1， 联立方程组得：{ 푦 = −푥 + 1 푦 = −푥2 + 2푥 + 3 ， 解得：{ 푥1 = 3−√17 2 푦1 = −1+√17 2 或{ 푥2 = 3+√17 2 푦2 = −1−√17 2 ， ∴ 点푄的坐标为(3−√17 2 , −1+√17 2 )或(3+√17 2 , −1−√17 2 )， 综上所述：点푄的坐标为(2,  3)或(3−√17 2 , −1+√17 2 )或(3+√17 2 , −1−√17 2 )．