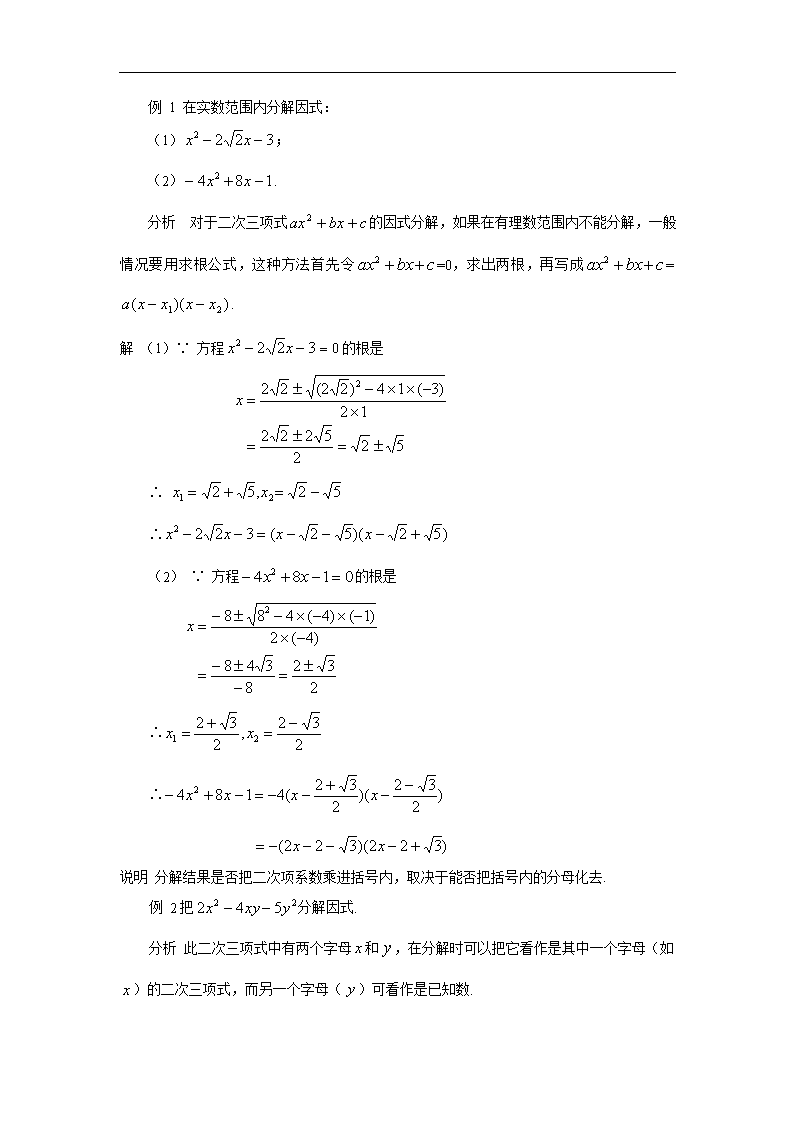中考数学专题复习练习：二次三项式的因式分解 8页

例 1 在实数范围内分解因式：‎ ‎（1）；‎ ‎（2）.‎ 分析 对于二次三项式的因式分解，如果在有理数范围内不能分解，一般情况要用求根公式，这种方法首先令=0，求出两根，再写成=.‎ 解 （1）∵ 方程的根是 ‎ ‎ ‎∴ ‎ ‎∴‎ ‎（2） ∵ 方程的根是 ‎ ‎ ‎∴‎ ‎∴‎ ‎ ‎ 说明 分解结果是否把二次项系数乘进括号内，取决于能否把括号内的分母化去.‎ 例 2把分解因式.‎ 分析 此二次三项式中有两个字母和，在分解时可以把它看作是其中一个字母（如）的二次三项式，而另一个字母（）可看作是已知数.‎ 解 ∵ 关于的方程的根是 ‎ ‎ ‎，‎ ‎∴‎ ‎∴‎ 说明 分解的结果不要丢掉两个一次因式里的.‎ 例3 当取何值时，二次三项式（1）在实数范围内能分解？（2）不能分解？（3）能分解成一个完全平方式？这个完全平方式是什么？‎ 分析 二次三项式能否分解的关键是对应的二次方程是否有解，而方程是否有解由其的符号决定.‎ 解 设 则 若，即时方程有两个不相等的实数根.‎ 此时在实数范围内能分解.‎ ‎（2）当时，不能分解.‎ ‎（3）当时，方程为.‎ ‎.‎ 此时为一个完全平方式.‎ 典型例题四 例 已知二次三项式分解因式为，则b、c的值为（ ）‎ A． B．‎ C． D．‎ 分析与解答 可利用多项式的因式分解是多项式乘法的逆变形这一关系解.‎ ‎ ‎ ‎∴ 且.‎ ‎∴ 选D.‎ 典型例题五 例 已知二次三项式是一个完全平方式，试求的值.‎ 分析：若二次三项式为一个完全平方式，则其相应方程的判别式 解 对于一元二次方程，其中，，，‎ 原二次三项式是一个完全平方式，‎ ‎ ，即 ‎，‎ 故当或时，二次三项式是一个完全平方式.‎ 说明：若，则二次三项式为完全平方式；反之，若为完全平方式，则.‎ 典型例题六 例 取何值时，方程（‎ 为有理数）的根为有理数？‎ 分析：根据一元二次方程的求根公式，若使方程的根为有理数，需使方程的判别式是关于的完全平方式，即为有理数；又根据二次三项式的因式分解公式知，若使为完全平方式，需使关于的方程的根，即方程的判别式，进而求得的值.‎ 解 把原方程化为一般式，得 若使方程有有理根，只需使为关于的完全平方式.‎ 若使是关于的完全平方式，需使 ‎，即 当时，方程有有理根.‎ 说明：上述求解中多次利用根的判别式，这里有一个结论，即二次三项式为完全平方式.‎ 典型例题七 例 在实数范围内分解因式：‎ 分析：在实数范围内分解二次三项式的问题，通常是采用公式法，在实数范围内分解因式，是指分解的结果中各因式的数字系数可以是实数范围内的任意实数.‎ 解 把原式化为 ‎，‎ 的两根为，，‎ 原式.‎ 说明：本题不是直接给出二次三项式要求分解因式，而是需要综合运用因式分解的方法进行分解.对于题中所给的多项式，若直接展开后重新分组分解，则计算量较大，且有一定的难度.上述求解中，是注意到两个二次三项式中仅一次项不同，采用了整体代换方法构造出含的二次三项式，从而达到分解因式的目的.同时，因式分解要分解到每一个因式都不能再分解之止.‎ 选择题 ‎1．是以下那个多项式分解因式形成的（ ）‎ A． B．‎ C． D．‎ ‎2. 分解因式：（）‎ A． B．‎ C． D．‎ ‎3．在实数范围内分解因式，正确的结果是（ ）‎ A． B．‎ C． D．‎ ‎4. 以与为根的一元二次方程是（）‎ A． B．‎ C． D．‎ ‎5. 分解因式：（）‎ A． B．‎ C． D．‎ ‎6. 分解因式：（）‎ A． B．‎ C． D．‎ ‎7. 分解因式：（）‎ A． B．‎ C． D．‎ ‎8. 若一元二次方程的两根为和4，则二次三项式可分解为（）‎ A． B．‎ C． D．‎ ‎9．多项式在实数范围内分解因式正确的结果是（ ）‎ A．‎ B．‎ C．‎ D．‎ 答案：‎ ‎1. A; 2. D 3. B ;4. A ;5. D;6. A; 7. B; 8. B; 9. B.‎ 判断题 ‎1. 是关于的二次三项式。（）‎ ‎2.不一定是关于的二次多项式。（）‎ ‎3. 方程的二根为，，则（）.‎ ‎4. .‎ ‎5..‎ ‎6.（）.‎ ‎7.‎ ‎（）.‎ ‎8. 在实数范围内分解因式：（）‎ ‎9.方程可变形为。（）‎ ‎10.二次三项式在实数范围内总能分解因式。（）‎ 答案：‎ ‎1．√；2.√;3. √ 4. ×; 5. × 6. √ 7. ×8. × 9. √; 10 .×.‎ 解答题 ‎1．分解因式：‎ ‎（1）；（2）；（3）.‎ ‎2．已知二次三项式是一个完全平方式，求m的值。‎ ‎3．在实数范围内分解因式。‎ ‎4．已知多项式分解因式后，有一因式是，请把多项式分解因式。‎ ‎5．已知，且，，求的值。‎ ‎6．已知，，求的值。‎ ‎7．设、为整数，且是6的倍数，求证：是18的倍数。‎ 答案：‎ ‎1．（1）;‎ ‎（2）;‎ ‎(3) .‎ ‎2．‎ ‎∵ 原二次三项式是完全平方式，‎ ‎∴ 。‎ ‎3．‎ ‎4．提示：用待定系数法。‎ 设 展开比较系数可解得 ‎ ‎ ‎5．0 3．‎ ‎6．即是6的倍数，是3的倍数，所以是18的倍数.‎