中考数学专题复习练习：平行线等分线段定理 11页

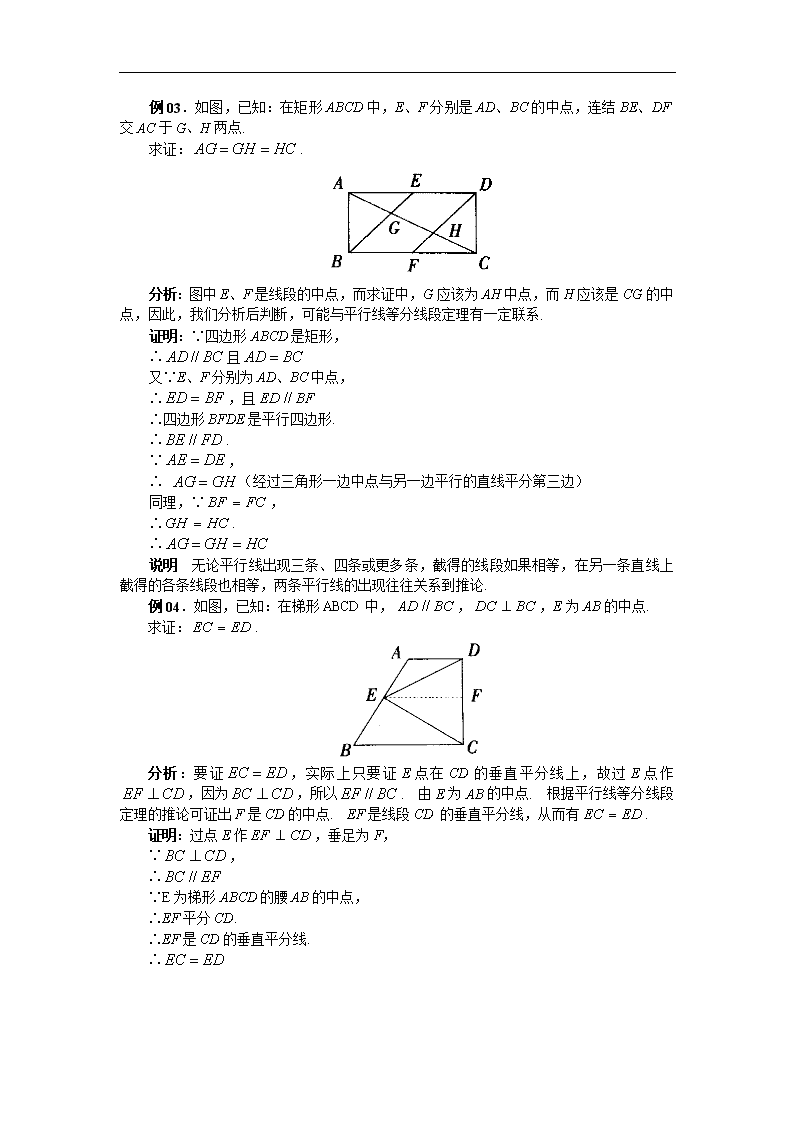
例01．如图，在中，AD是BC边上的中线，M是AD的中点，BM的延长线交AC于N. ‎ 求证：‎ 证明：过点D作，交AC于E. ‎ ‎∵D为BC中点，‎ ‎∴. ‎ ‎∵M为AD中点，，‎ ‎∴. ‎ ‎∴，‎ 即 说明：本题考查平行线等分线段定理的推论，解题关键是过中点D作BN的平行线DE交AC于E，证出E是NC的中点. ‎ 例02．如图，已知：在梯形ABCD中，，，交DC于F，AF、BC延长线交于点G. ‎ 求证：. ‎ 分析：因为，所以为了证明只需证明就可以了. 那么由很容易得到这点. ‎ 证明 ∵（已知），‎ ‎∴ （如果两条直线都平行于第三条直线，则这两条直线平行）‎ 又∵ （已知）‎ ‎∴ （经过三角形一边的中点与另一边平行的直线必平分第三边）‎ ‎（经过梯形一腰的中点与底平行的直线，必平分另一腰）‎ 又∵， ‎ ‎∴ ‎ ‎∴ ‎ ‎∴ ‎ 例03．如图，已知：在矩形ABCD中，E、F分别是AD、BC的中点，连结BE、DF交AC于G、H两点. ‎ 求证：. ‎ 分析：图中E、F是线段的中点，而求证中，G应该为AH中点，而H应该是CG的中点，因此，我们分析后判断，可能与平行线等分线段定理有一定联系. ‎ 证明：∵四边形ABCD是矩形，‎ ‎∴且 又∵E、F分别为AD、BC中点，‎ ‎∴，且 ‎∴四边形BFDE是平行四边形. ‎ ‎∴. ‎ ‎∵，‎ ‎∴ （经过三角形一边中点与另一边平行的直线平分第三边）‎ 同理，∵，‎ ‎∴. ‎ ‎∴‎ 说明 无论平行线出现三条、四条或更多条，截得的线段如果相等，在另一条直线上截得的各条线段也相等，两条平行线的出现往往关系到推论. ‎ 例04．如图，已知：在梯形ABCD中，，，E为AB的中点. ‎ 求证：. ‎ 分析：要证，实际上只要证E点在CD的垂直平分线上，故过E点作，因为，所以. 由E为AB的中点. 根据平行线等分线段定理的推论可证出F是CD的中点. EF是线段CD 的垂直平分线，从而有. ‎ 证明：过点E作，垂足为F，‎ ‎∵，‎ ‎∴‎ ‎∵E为梯形ABCD的腰AB的中点，‎ ‎∴EF平分CD. ‎ ‎∴EF是CD的垂直平分线. ‎ ‎∴‎ 例05．如图，，M是DC的中点. ‎ 求证：. ‎ 证法1 作于N. ‎ ‎∵，‎ ‎∴‎ ‎∵,‎ ‎∴. ‎ ‎∴MN垂直平分AB，‎ 故 证法2 如图，延长BM交AD于P. ‎ ‎∵，‎ ‎∴. ‎ ‎∴‎ ‎∵，‎ ‎∴. ‎ ‎∴ ‎ ‎∴AM是斜边PB的中线. ‎ ‎∴. ‎ 说明 证法1是运用平分线等分线段定理证明的，证法2则是用补全基本图形的方法运用直角三角形斜边中线等于斜边一半证明的. ‎ 例06．如图，梯形ABCD中，，，，，E为AB的中点. ‎ 求证：为等边三角形. ‎ 证明 过点E作. ‎ ‎∵，‎ ‎∴‎ ‎∵E为AB的中点，‎ ‎∴F为CD的中点. ‎ ‎∵，，‎ ‎∴ ∴‎ ‎∵，‎ ‎∴为等边三角形. ‎ ‎∴‎ ‎∵E为AB的中点，‎ ‎∴‎ ‎∴ ‎ ‎∴ ‎ ‎∵，‎ ‎∴为等边三角形. ‎ 说明 本题综合考查了平行线等分线段定理的推论及等边三角形的判定与性质，解题关键是作辅助线. ‎ 例07．如图，有一块直角三角形菜地，分配给张、王、李三家农户耕地. 已知张、王、李三家人口分别为2人，4人，6人，菜地分配方法要按人口比例，并要求每户土地均有一部分紧靠水渠AB. P点处是三家合用的肥料仓库，所以P点必须是三家地的交界处. 已知的，米，. （1）计算出每家应分配的菜地面积；（2）用尺规在图中作出各家菜地的分界线（保留痕迹，不写作法，标出户名）. ‎ 解答：（1）在中，‎ ‎∵，‎ ‎∴. ‎ ‎∴（米）‎ ‎∴（米）‎ ‎（米）‎ ‎∵‎ ‎∴（）‎ ‎（）‎ ‎（）‎ ‎（2）运用平行线等分线段的方法作出图形如图. ‎ 说明：本题考查了平行线等分线段定理的应用，解题的易错点是忽视运用的直角三角形的性质，关键是运用平行线等分线段定理的作图. ‎ 选择题 ‎1．下列用平行线等分线段的图形中，错误的是（ ）‎ ‎2．如图，在线段AB上取一点C，使. 作法正确的是（ ）‎ ‎3．（福州市，2001）下列四个命题中错误的是（ ）‎ ‎ A．两条对角线互相垂直且相等的四边形是正方形 B．菱形的一条对角线平分一组对角 C．顺次连结四边形的各边中点所得的四边形是平行四边形 D．等腰梯形的两条对角线相等 ‎4．（北京市朝阳区，2001）顺次连结任意四边形各边中点所得的四边形是（ ）‎ ‎ A．平行四边形 B．矩形 C．菱形 D．正方形 ‎5．如图，，且，，则（ ）‎ A．9 B．10 C．11 D．12‎ ‎6．AD是锐角的高，，M，N在AB上，且，于E，于F，则（ ）‎ A． B． C． D．‎ ‎7．（哈尔滨市，2001）直角三角形的两条直角边长分别为和，则连结这两条直角边中点线段的长为（ ）‎ A．3 B．4 C．5 D．12‎ ‎8．（绍兴市，2001）如图，中，D、E分别是边BC、AC的中点，若，则AB等于（ ）‎ A． B．6 C．9 D．‎ ‎9．等腰的底边BC是周长的，自底边上任意一点P引平行于两腰的直线，分别交两腰于E，F，则四边形AEPF的周长与的周长之比为（）‎ A． B． C． D．‎ 参考答案：‎ ‎1．C 2．D 3．A 4．A 5．A 6．A 7．C 8．B 9．C ‎ 填空题 ‎1．如图，，，则_____＝___＝_____，______＝______. ‎ ‎2．如图，已知，AF，BE交于O，若，‎ ‎，则_______. ‎ ‎3．（北京市西城区，2001）以长为8，宽为6的矩形各边中点为顶点的四边形的周长为______. ‎ ‎4．（厦门市，2001）如图，梯形ABCD中，，且，梯形ABCD的面积是，点M、N分别是AD和BC上一点，E、F分别是BM、CM的中点，则四边形MENF的面积是______ . ‎ ‎5．（盐城市，2001）已知三角形的周长是，则以它的三条边中点为顶点所构成的三角形周长是______ . ‎ 参考答案：‎ ‎1．，，， ‎ ‎2．‎ ‎3．20 ‎ ‎4． ‎ ‎5．6 ‎ 解答题 ‎1．把线段AB五等分. ‎ ‎2．如图，在中，AD为BC边中线，F为AC上一点，，连结BF交AD于E，. 求BF的长. ‎ ‎3．如图，直角梯形ABCD中，，，M是CD的中点. ‎ 求证：. ‎ ‎4．用两种方法证明：‎ 如图，MN过顶点A，过B，C分别作于E，于F，D为BC中点. ‎ 求证：.‎ ‎5．如图，已知四边形ABCD为平行四边形，E是AD上一点，且CE平分，. ‎ 求证：. ‎ ‎6．（聊城市，2001）已知：如图，中，，D、E分别为AB、BC的中点，点F在AC的延长线上，. ‎ ‎（1）求证：；‎ ‎（2）若，，求四边形DCFE的面积. ‎ ‎7．如图，M，N分别是ABCD中AB，CD的中点. ‎ 求证：. ‎ ‎8．如图，中，CH是的平分线，于D，交AB于E. 求证：. ‎ ‎9．如图，等腰直角，，，交AB于F，交AB于G. ‎ 求证：. ‎ ‎10．如图，ABCD为梯形，，ADBE是平行四边形，AB的延长线交EC于F. ‎ 求证：. ‎ ‎11．已知：如图，AD平分，，垂足为D，并AC于E. ‎ 求证：. ‎ ‎12．如图，F为AB的中点，四边形CGFE为菱形，. ‎ 求证：D，F，H为线段AB的四等分点. ‎ ‎13．垂直放在地面上的镜子要多高，你就可以站在镜子前看到你的全身像？‎ 参考答案：‎ ‎1．略 ‎2．过D作交FC于M. . ‎ ‎3．证明：过点M作交AB于点N. ‎ ‎∴‎ ‎∵， ∴ . ‎ ‎∴ ∴‎ ‎4．证法1：过D作于G；用平行线等分线段定理证明；‎ 证法2：延长FD交EB的延长线于H.；用直角三角形斜边的中线等于斜边的一半证明.‎ ‎5．证法1：取BC的中点M，连EM，则EM是斜边上的中线. ‎ ‎∴. ∴‎ ‎∵. ∴‎ ‎∵，∴ 四边形EMCD是平行四边形. ‎ ‎∴. ∴ ∴‎ 证法2：如图，延长BE交CD的延长线于F. ‎ ‎∵，CE平分，∴ ‎ ‎∵，∴. ‎ ‎∵，∴. ‎ ‎6．（1）证；（2）12‎ ‎7．易证，‎ ‎8．延长AD交BC于F，可证. 因为,∴‎ ‎9．延长BC到H，使，连AH，则，∴∵，∴. ∴ ∵，∴‎ ‎10．连结DE并交AB于O. ，，∴ ‎ ‎11．证明：延长CD交AB于F. 在和中，‎ ‎∵，，，‎ ‎∴，∴‎ 又∵，∴ ‎ 又∵，∴. ‎ ‎12．∵F是AB中点，，∴G为A中点. 同理E为BC中点. 因，则. 同理. 由E，G为中点，可得D为BF中点，H为AF中点 ‎13．当镜子高度为一个人高度的一半