2009中考数学分类汇编-平面直角坐标系(简） 7页

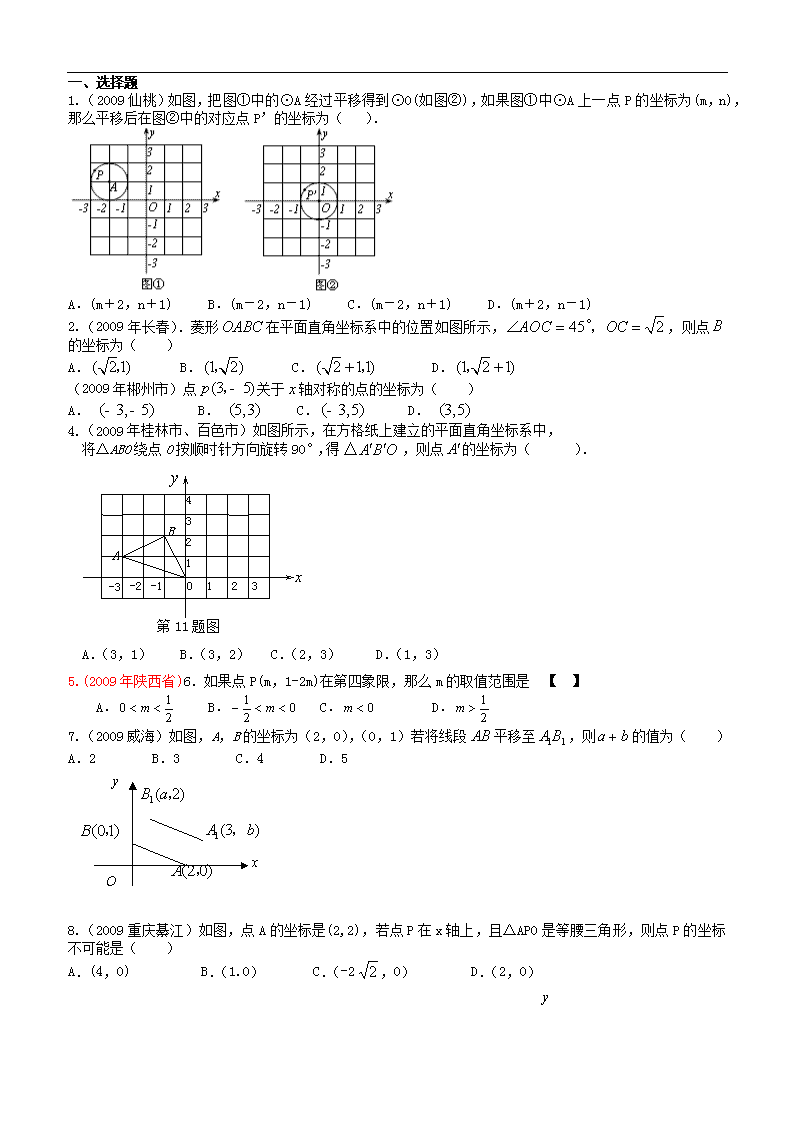
一、选择题 ‎1.（2009仙桃）如图，把图①中的⊙A经过平移得到⊙O(如图②)，如果图①中⊙A上一点P的坐标为(m，n)，那么平移后在图②中的对应点P’的坐标为（ ）．‎ A．(m＋2，n＋1) B．(m－2，n－1) C．(m－2，n＋1) D．(m＋2，n－1)‎ ‎2.（2009年长春）．菱形在平面直角坐标系中的位置如图所示，，则点的坐标为（ ）‎ A． B． C． D．‎ ‎（2009年郴州市）点关于轴对称的点的坐标为（　　）‎ A． B． C． D． ‎ ‎4.（2009年桂林市、百色市）如图所示，在方格纸上建立的平面直角坐标系中，‎ 将△ABO绕点O按顺时针方向旋转90°，得 ，则点的坐标为（ ）． ‎ ‎1‎ ‎2‎ ‎4‎ ‎3‎ ‎0‎ ‎-1‎ ‎-2‎ ‎-3‎ ‎1‎ ‎2‎ ‎3‎ A B 第11题图 A．（3，1） B．（3，2） C．（2，3） D．（1，3）‎ ‎5.(2009年陕西省)6．如果点P(m，1‎-2m)在第四象限，那么m的取值范围是 【 】‎ A． B． C． D．‎ ‎7.（2009威海）如图，A，B的坐标为（2，0），（0，1）若将线段平移至，则的值为（　　）‎ A．2 B．‎3 ‎ C．4 D．5‎ y O x ‎8.（2009重庆綦江）如图，点A的坐标是(2,2)，若点P在x轴上，且△APO是等腰三角形，则点P的坐标不可能是（ ）‎ A．(4，0) B．（1.0） y C．（-2，0） D．（2，0）‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎-1‎ ‎1‎ ‎2‎ x y A ‎0‎ ‎9.（2009年崇左）已知点的坐标为，为坐标原点，连结，将线段绕点按逆时针方向旋转90°得，则点的坐标为（ ）．‎ A． B． C． D．‎ ‎10. （2009襄樊市）如图3，在边长为1的正方形网格中，将向右平移两个单位长度得到则与点关于轴对称的点的坐标是（ D ）‎ A．　B． C． D．‎ ‎ ‎ ‎13.（2009年杭州市） 有以下三个说法：①坐标的思想是法国数学家笛卡儿首先建立的；②除了平面直角坐标系外，我们也可以用方向和距离来确定物体的位置；③平面直角坐标系内的所有点都分别属于四个象限．其中错误的是（ ）‎ A．只有① B．只有② C．只有③ D．①②③‎ ‎14.（2009年杭州市） 已知点P（，）在函数的图象上，那么点P应在平面直角坐标系中的（ ）‎ A．第一象限 B． 第二象限 C． 第三象限 D． 第四象限 ‎16. （2009年嘉兴市）沪杭高速铁路已开工建设，某校研究性学习以此为课题，在研究列车的行驶速度时，得到一个数学问题．如图，若是关于的函数，图象为折线，其中，，，四边形的面积为70，则（　▲　）‎ A． B． C． D．‎ ‎17.（2009年天津市）在平面直角坐标系中，已知线段的两个端点分别是，将线段平移后得到线段，若点的坐标为，则点的坐标为（ ）‎ A．　　　B．　　 C．　　　D．‎ ‎18. （2009年湘西自治州）12.在直角坐标系中，点M（sin50°，－cos70°）所在的象限是（　　）‎ A． 第一象限 B． 第二象限 C． 第三象限 D． 第四象限 ‎19. （2009年广西钦州）点P（－2，1）关于 y轴对称的点的坐标为（ ）‎ ‎ A．（－2，－1） B．（2，1） C．（2，－1） D．（－2，1）‎ ‎20. (2009年南充)在平面直角坐标系中，点与点B关于轴对称，则点B的坐标是（ ）‎ A． B． C． D．‎ ‎22. （09湖南邵阳）在平面直角坐标系中，函数的图象经过（ ）‎ A．一、二、三象限 B．二、三、四象限 C．一、三、四象限 D．一、二、四象限 二、填空题 ‎1. （2009湖北省荆门市）将点P向左平移2个单位，再向上平移1个单位得到（，3），则点P的坐标是______．‎ ‎2．（2009年浙江省绍兴市）如图是绍兴市行政区域图，若上虞市区所在地用坐标表示为，诸暨市区所在地用坐标表示为，那么嵊州市区所在地用坐标可表示为______________．‎ ‎ ‎ ‎ ‎ ‎4.（2009泰安）如图所示，△A’B’C’是由△ABC向右平移5个单位，然后绕B点逆时针旋转90°得到的（其中A’、B’、C’的对应点分别是A、B、C），点A’的坐标是（4，4）点B’的坐标是（1，1），则点A的坐标是 。‎ ‎6.（2009年新疆）如图，在平面直角坐标系中，已知一圆弧过小正方形网格的格点，已知点的坐标是，则该圆弧所在圆的圆心坐标是___________．‎ y x O A B C ‎7. （2009白银市）14.反比例函数的图象经过点P（，1），则这个函数的图象位于第　　　　象限．‎ ‎9. 2．（2009年广西梧州）将点A（1，－3）向右平移2个单位，再向下平移2个单位后得到点B（a，b），‎ 则ab＝ ★ ．‎ ‎10. （2009年包头）线段是由线段平移得到的，点的对应点为，则点的对应点的坐标是 ． ‎ ‎11. （2009肇庆）11．在平面直角坐标系中，点关于原点对称点的坐标是 ． ‎ ‎12. (2009年湖州)已知抛物线（＞0）的对称轴为直线，且经过点试比较和的大小：‎ ‎ _（填“>”，“<”或“=”）‎ ‎15. （2009年湖北十堰市）如图，在平面直角坐标系中，点A的坐标为(1，4)，将线段OA绕点O顺时针旋转90°得到线段OA′，则点A′的坐标是 ．‎ ‎16. （2009年新疆乌鲁木齐市）在平面直角坐标系中，点在第四象限，则实数的取值范围是 ．‎ ‎17. （2009年山西省）如图，与是位似图形，且顶点都在格点上，则位似中心的坐标是 ．‎ x O A B C ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎21.(2009年绵阳)如图是由若干个边长为1的小正方形组成的网格，请在图中作出将“蘑菇”ABCDE绕A点逆时针旋转90°再向右平移2个单位的图形（其中C、D为所在小正方形边的中点）．‎ A B E C D ‎22.（2009年常德市）如图2，△ABC向右平移4个单位后得到△A′B′C′，则A′点的坐标是 　 ．‎ 图2‎ ‎ ‎ ‎23. （2009年内蒙古包头）线段是由线段平移得到的，点的对应点为，则点 的对应点的坐标是 ．‎ 三、解答题 ‎1．（2009年长春）如图，点的坐标为，过点作轴的平行线交轴于点，交双曲线（）于点，作交双曲线（）于点，连结．已知．‎ y x O P A M N ‎（1）求的值．（3分）‎ ‎（2）求的面积．（3分）‎ ‎2. （2009年锦州）△ABC在平面直角坐标系中的位置如图8所示，其中每个小正方形的边长为1个单位长度. ‎ ‎　　(1)将△ABC向右移平2个单位长度，作出平移后的△A1B‎1C1，并写出△A1B‎1C1各顶点的坐标；‎ ‎　　(2)若将△ABC绕点(-1,0)顺时针旋转180°后得到△A2B‎2C2，并写出△A2B‎2C2各顶点的坐标；‎ ‎(3)观察△A1B‎1C1和△A2B‎2C2，它们是否关于某点成中心对称？若是，请写出对称中心的坐标；若不是，说明理由.‎ ‎4.（2009年齐齐哈尔市）如图，在平面直角坐标系中，的顶点坐标为、、．‎ ‎（1）若将向右平移3个单位长度，再向上平移1个单位长度，请画出平移后的；‎ ‎（2）画出绕原点旋转后得到的；‎ ‎（3）与是中心对称图形，请写出对称中心的坐标：___________；‎ ‎（4）顺次连结，所得到的图形是轴对称图形吗？‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎1‎ ‎2‎ ‎4‎ ‎3‎ y x O A B C ‎′‎ ‎′‎ ‎′‎ ‎6.（2009年天津市）已知一个直角三角形纸片，其中 ‎．如图，将该纸片放置在平面直角坐标系中，折叠该纸片，折痕与边交于点，与边交于点．‎ ‎（Ⅰ）若折叠后使点与点重合，求点的坐标；‎ x y B O A ‎（Ⅱ）若折叠后点落在边上的点为，设，，试写出关于的函数解析式，并确定的取值范围；‎ x y B O A ‎（Ⅲ）若折叠后点落在边上的点为，且使，求此时点的坐标． ‎ x y B O A ‎7. (2009年牡丹江市)如图，□ABCD在平面直角坐标系中，若、的长是关于的一元二次方程的两个根，且 ‎（1）求的值．‎ ‎（2）若为轴上的点，且求经过、两点的直线的解析式，并判断与是否相似？‎ ‎（3）若点在平面直角坐标系内，则在直线上是否存在点使以、、、为顶点的四边形为菱形？若存在，请直接写出点的坐标；若不存在，请说明理由．‎ x y A D B O C ‎28题图 ‎8．(2009年南充)如图，在平面直角坐标系中，已知点，轴于A．‎ ‎（1）求的值；‎ ‎（2）将点B绕原点逆时针方向旋转90°后记作点，求点的坐标；‎ ‎（3）将平移得到，点A的对应点是，点的对应点的坐标为，在坐标系中作出，并写出点、的坐标．‎ O x A B ‎1‎ ‎1‎ y ‎9. （2009年茂名市）18．如图，方格中有一个请你在方格内，画出满足条件 的并判断与是否一定全等？‎ B A C