北京市2008-2019年中考数学分类汇编图形性质pdf含解析 34页

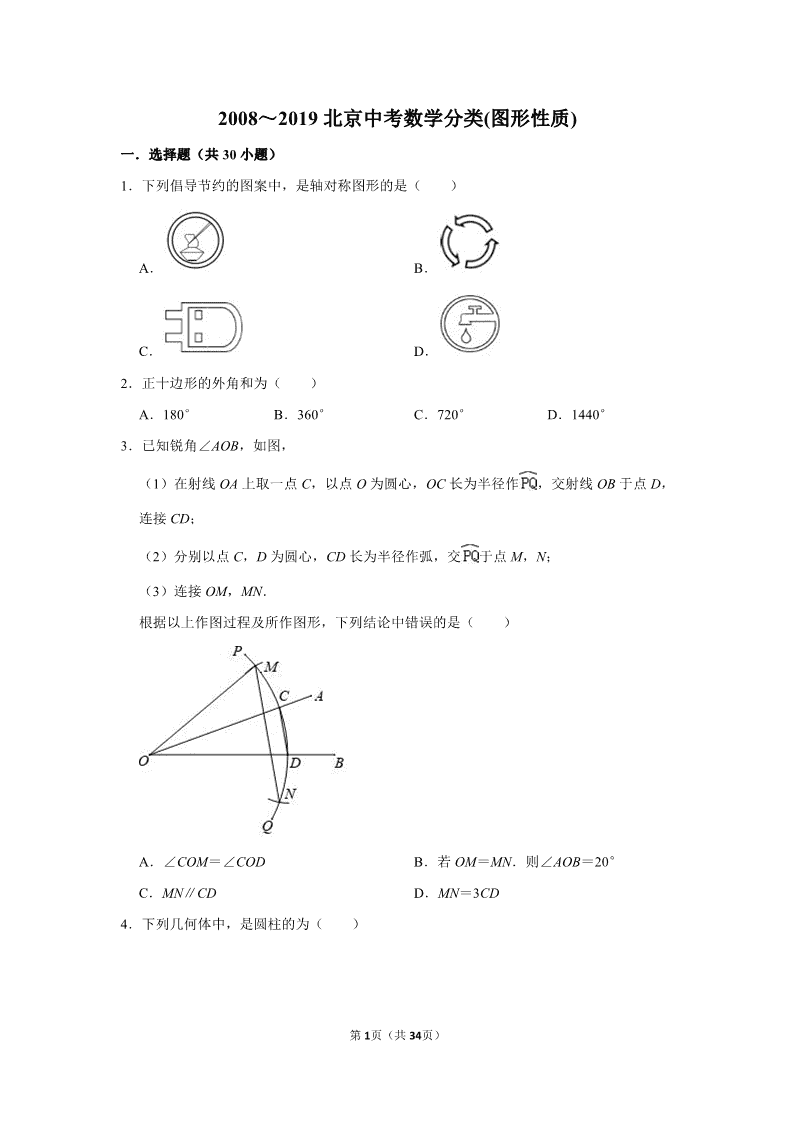
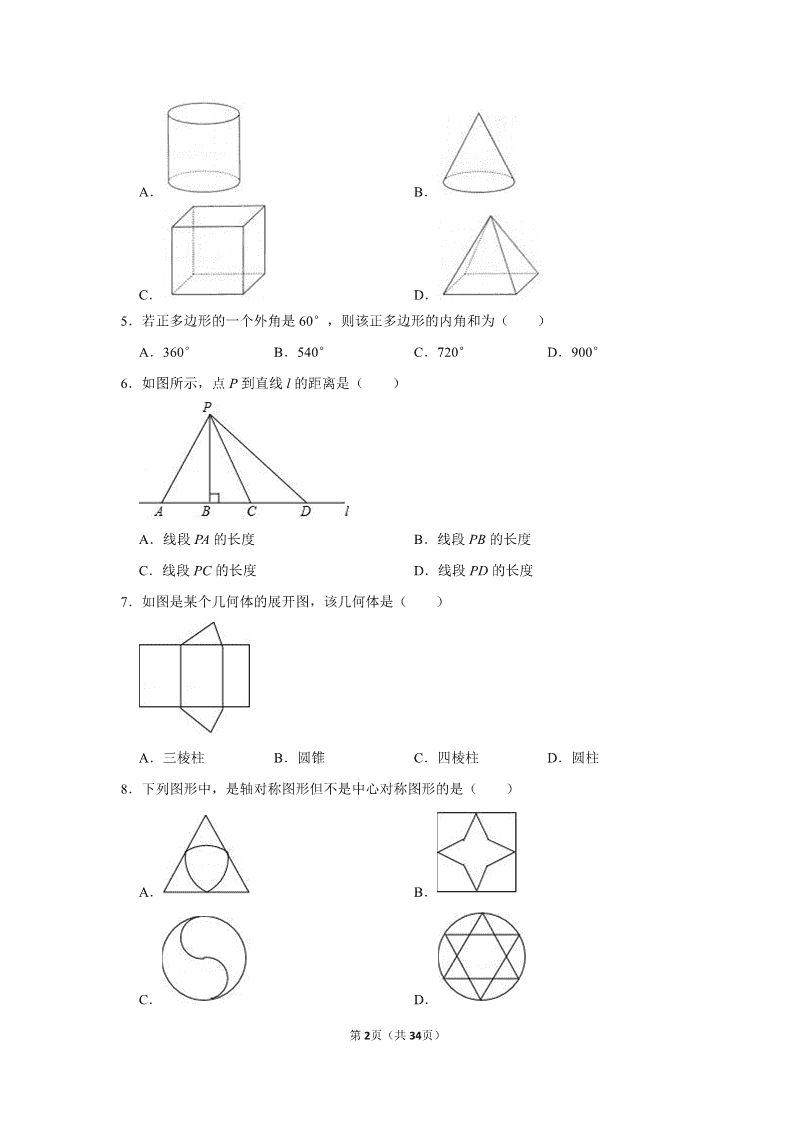
第 1页（共 34页） 2008～2019 北京中考数学分类(图形性质) 一．选择题（共 30 小题） 1．下列倡导节约的图案中，是轴对称图形的是（ ） A． B． C． D． 2．正十边形的外角和为（ ） A．180° B．360° C．720° D．1440° 3．已知锐角∠AOB，如图， （1）在射线 OA 上取一点 C，以点 O 为圆心，OC 长为半径作 ，交射线 OB 于点 D， 连接 CD； （2）分别以点 C，D 为圆心，CD 长为半径作弧，交 于点 M，N； （3）连接 OM，MN． 根据以上作图过程及所作图形，下列结论中错误的是（ ） A．∠COM＝∠COD B．若 OM＝MN．则∠AOB＝20° C．MN∥CD D．MN＝3CD 4．下列几何体中，是圆柱的为（ ） 第 2页（共 34页） A． B． C． D． 5．若正多边形的一个外角是 60°，则该正多边形的内角和为（ ） A．360° B．540° C．720° D．900° 6．如图所示，点 P 到直线 l 的距离是（ ） A．线段 PA 的长度 B．线段 PB 的长度 C．线段 PC 的长度 D．线段 PD 的长度 7．如图是某个几何体的展开图，该几何体是（ ） A．三棱柱 B．圆锥 C．四棱柱 D．圆柱 8．下列图形中，是轴对称图形但不是中心对称图形的是（ ） A． B． C． D． 第 3页（共 34页） 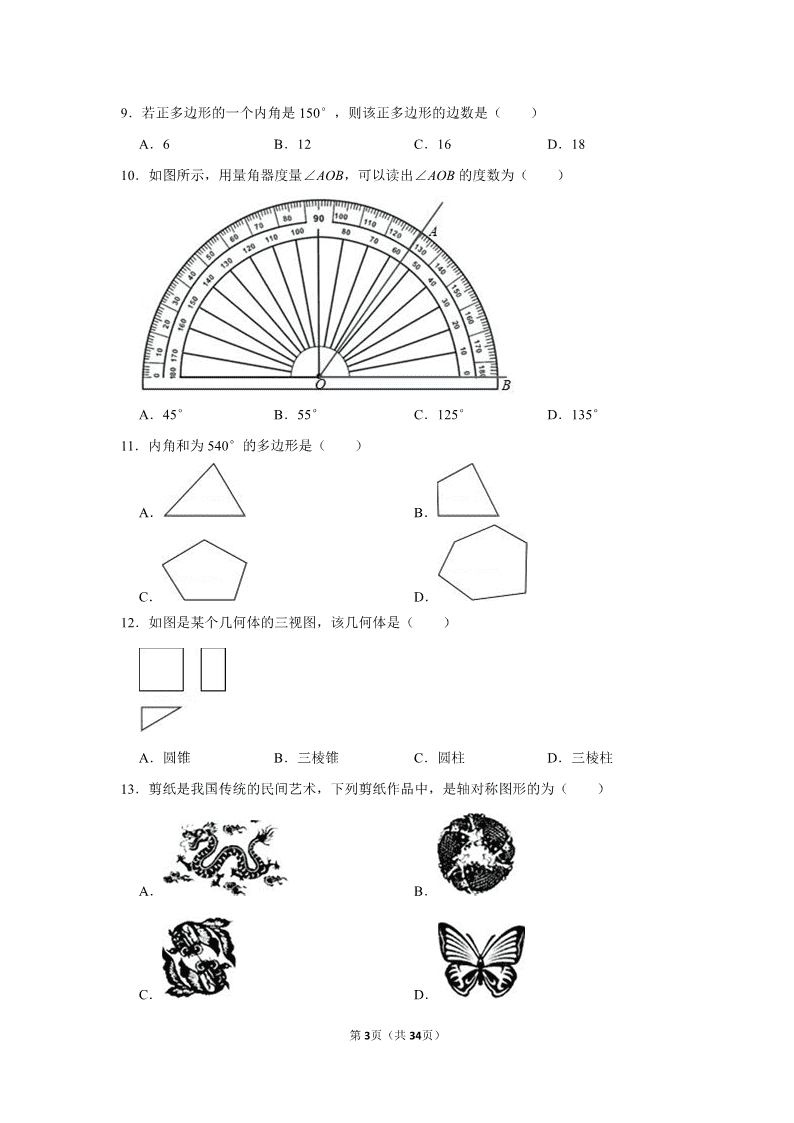9．若正多边形的一个内角是 150°，则该正多边形的边数是（ ） A．6 B．12 C．16 D．18 10．如图所示，用量角器度量∠AOB，可以读出∠AOB 的度数为（ ） A．45° B．55° C．125° D．135° 11．内角和为 540°的多边形是（ ） A． B． C． D． 12．如图是某个几何体的三视图，该几何体是（ ） A．圆锥 B．三棱锥 C．圆柱 D．三棱柱 13．剪纸是我国传统的民间艺术，下列剪纸作品中，是轴对称图形的为（ ） A． B． C． D． 第 4页（共 34页） 14．如图，直线 l1，l2，l3 交于一点，直线 l4∥l1，若∠1＝124°，∠2＝88°，则∠3 的度 数为（ ） A．26° B．36° C．46° D．56° 15．如图，公路 AC，BC 互相垂直，公路 AB 的中点 M 与点 C 被湖隔开．若测得 AM 的长 为 1.2km，则 M，C 两点间的距离为（ ） A．0.5km B．0.6km C．0.9km D．1.2km 16．如图是几何体的三视图，该几何体是（ ） A．圆锥 B．圆柱 C．正三棱柱 D．正三棱锥 17．如图， ⊙ O 的直径 AB 垂直于弦 CD，垂足为 E，∠A＝22.5°，OC＝4，CD 的长为 （ ） A．2 B．4 C．4 D．8 18．如图，直线 a，b 被直线 c 所截，a∥b，∠1＝∠2，若∠3＝40°，则∠4 等于（ ） 第 5页（共 34页） A．40° B．50° C．70° D．80° 19．如图，为估算某河的宽度，在河对岸选定一个目标点 A，在近岸取点 B，C，D，使得 AB⊥BC，CD⊥BC，点 E 在 BC 上，并且点 A，E，D 在同一条直线上．若测得 BE＝20m， CE＝10m，CD＝20m，则河的宽度 AB 等于（ ） A．60m B．40m C．30m D．20m 20．下列图形中，是中心对称图形，但不是轴对称图形的是（ ） A． B． C． D． 21．正十边形的每个外角等于（ ） A．18° B．36° C．45° D．60° 22．如图是某个几何体的三视图，该几何体是（ ） A．长方体 B．正方体 C．圆柱 D．三棱柱 23．如图，直线 AB，CD 交于点 O，射线 OM 平分∠AOC，若∠BOD＝76°，则∠BOM 等 于（ ） 第 6页（共 34页） A．38° B．104° C．142° D．144° 24．下列图形中，既是中心对称又是轴对称图形的是（ ） A．等边三角形 B．平行四边形 C．梯形 D．矩形 25．如图，在梯形 ABCD 中，AD∥BC，对角线 AC，BD 相交于点 O，若 AD＝1，BC＝3， 则 的值为（ ） A． B． C． D． 26．如图，在△ABC 中，点 D、E 分 AB、AC 边上，DE∥BC，若 AD：AB＝3：4，AE＝6， 则 AC 等于（ ） A．3 B．4 C．6 D．8 27．若菱形两条对角线的长分别为 6 和 8，则这个菱形的周长为（ ） A．20 B．16 C．12 D．10 28．一个几何体的三视图如图所示，这个几何体是（ ） A．棱柱 B．正方形 C．圆柱 D．圆锥 29．若一个正多边形的一个外角是 40°，则这个正多边形的边数是（ ） A．10 B．9 C．8 D．6 30．若一个多边形的内角和等于 720°，则这个多边形的边数是（ ） 第 7页（共 34页） A．5 B．6 C．7 D．8 二．填空题（共 20 小题） 31．如图，已知△ABC，通过测量、计算得△ABC 的面积约为 cm2．（结果保留一位 小数） 32．在如图所示的几何体中，其三视图中有矩形的是 ．（写出所有正确答案的序号） 33．如图所示的网格是正方形网格，则∠PAB+∠PBA＝ °（点 A，B，P 是网格线交 点）． 34．把图 1 中的菱形沿对角线分成四个全等的直角三角形，将这四个直角三角形分别拼成如 图 2，图 3 所示的正方形，则图 1 中菱形的面积为 ． 35．在矩形 ABCD 中，M，N，P，Q 分别为边 AB，BC，CD，DA 上的点（不与端点重合）， 对于任意矩形 ABCD，下面四个结论中， ① 存在无数个四边形 MNPQ 是平行四边形； ② 存在无数个四边形 MNPQ 是矩形； ③ 存在无数个四边形 MNPQ 是菱形； ④ 至少存在一个四边形 MNPQ 是正方形． 第 8页（共 34页） 所有正确结论的序号是 ． 36．如图所示的网格是正方形网格，∠BAC ∠DAE．（填“＞”，“＝”或“＜”） 37．如图，点 A，B，C，D 在 ⊙ O 上， ＝ ，∠CAD＝30°，∠ACD＝50°，则∠ADB ＝ ． 38．如图，在矩形 ABCD 中，E 是边 AB 的中点，连接 DE 交对角线 AC 于点 F，若 AB＝4， AD＝3，则 CF 的长为 ． 39．如图，在△ABC 中，M、N 分别为 AC，BC 的中点．若 S△CMN＝1，则 S 四边形 ABNM＝ ． 40．如图，AB 为 ⊙ O 的直径，C、D 为 ⊙ O 上的点， ＝ ．若∠CAB＝40°，则∠CAD ＝ ． 第 9页（共 34页） 41．如图，在平面直角坐标系 xOy 中，△AOB 可以看作是△OCD 经过若干次图形的变化（平 移、轴对称、旋转）得到的，写出一种由△OCD 得到△AOB 的过程： ． 42．如图，小军、小珠之间的距离为 2.7m，他们在同一盏路灯下的影长分别为 1.8m，1.5m， 已知小军、小珠的身高分别为 1.8m，1.5m，则路灯的高为 m． 43．如图是由射线 AB，BC，CD，DE，EA 组成的平面图形，则∠1+∠2+∠3+∠4+∠5＝ ． 44．在某一时刻，测得一根高为 1.8m 的竹竿的影长为 3m，同时测得一根旗杆的影长为 25m， 那么这根旗杆的高度为 m． 45．如图，O 是矩形 ABCD 的对角线 AC 的中点，M 是 AD 的中点．若 AB＝5，AD＝12， 则四边形 ABOM 的周长为 ． 第 10页（共 34页） 46．如图，小明同学用自制的直角三角形纸板 DEF 测量树的高度 AB，他调整自己的位置， 设法使斜边 DF 保持水平，并且边 DE 与点 B 在同一直线上．已知纸板的两条直角边 DE ＝40cm，EF＝20cm，测得边DF离地面的高度AC＝1.5m，CD＝8m，则树高AB＝ m． 47．若下图是某几何体的表面展开图，则这个几何体是 ． 48．如图，AB 为圆 O 的直径，弦 CD⊥AB，垂足为点 E，连接 OC，若 OC＝5，CD＝8， 则 AE＝ ． 49．如图，AB 为 ⊙ O 的直径，弦 CD⊥AB，E 为 上一点，若∠CEA＝28°，则∠ABD＝ 度． 50．如图，正方形纸片 ABCD 的边长为 1，M、N 分别是 AD、BC 边上的点，将纸片的一角 沿过点 B 的直线折叠，使 A 落在 MN 上，落点记为 A′，折痕交 AD 于点 E，若 M、N 分别是 AD、BC 边的中点，则 A′N＝ ；若 M、N 分别是 AD、BC 边的上距 DC 第 11页（共 34页） 最近的 n 等分点（n≥2，且 n 为整数），则 A′N＝ （用含有 n 的式子表示）． 第 12页（共 34页） 2008～2019 北京中考数学分类(图形性质) 参考答案与试题解析 一．选择题（共 30 小题） 1．下列倡导节约的图案中，是轴对称图形的是（ ） A． B． C． D． 【解答】解：A、不是轴对称图形，故此选项错误； B、不是轴对称图形，故此选项错误； C、是轴对称图形，故此选项正确； D、不是轴对称图形，故此选项错误． 故选：C． 2．正十边形的外角和为（ ） A．180° B．360° C．720° D．1440° 【解答】解：因为任意多边形的外角和都等于 360°， 所以正十边形的外角和等于 360°，． 故选：B． 3．已知锐角∠AOB，如图， （1）在射线 OA 上取一点 C，以点 O 为圆心，OC 长为半径作 ，交射线 OB 于点 D， 连接 CD； （2）分别以点 C，D 为圆心，CD 长为半径作弧，交 于点 M，N； （3）连接 OM，MN． 根据以上作图过程及所作图形，下列结论中错误的是（ ） 第 13页（共 34页） A．∠COM＝∠COD B．若 OM＝MN．则∠AOB＝20° C．MN∥CD D．MN＝3CD 【解答】解：由作图知 CM＝CD＝DN， ∴∠COM＝∠COD，故 A 选项正确； ∵OM＝ON＝MN， ∴△OMN 是等边三角形， ∴∠MON＝60°， ∵CM＝CD＝DN， ∴∠MOA＝∠AOB＝∠BON＝ ∠MON＝20°，故 B 选项正确； 设∠MOA＝∠AOB＝∠BON＝ α ， 则∠OCD＝∠OCM＝ ， ∴∠MCD＝180°﹣ α ， 又∵∠CMN＝ ∠CON＝ α ， ∴∠MCD+∠CMN＝180°， ∴MN∥CD，故 C 选项正确； 第 14页（共 34页） ∵MC+CD+DN＞MN，且 CM＝CD＝DN， ∴3CD＞MN，故 D 选项错误； 故选：D． 4．下列几何体中，是圆柱的为（ ） A． B． C． D． 【解答】解：A、此几何体是圆柱体； B、此几何体是圆锥体； C、此几何体是正方体； D、此几何体是四棱锥； 故选：A． 5．若正多边形的一个外角是 60°，则该正多边形的内角和为（ ） A．360° B．540° C．720° D．900° 【解答】解：该正多边形的边数为：360°÷60°＝6， 该正多边形的内角和为：（6﹣2）×180°＝720°． 故选：C． 6．如图所示，点 P 到直线 l 的距离是（ ） A．线段 PA 的长度 B．线段 PB 的长度 C．线段 PC 的长度 D．线段 PD 的长度 【解答】解：由题意，得 点 P 到直线 l 的距离是线段 PB 的长度， 第 15页（共 34页） 故选：B． 7．如图是某个几何体的展开图，该几何体是（ ） A．三棱柱 B．圆锥 C．四棱柱 D．圆柱 【解答】解：观察图形可知，这个几何体是三棱柱． 故选：A． 8．下列图形中，是轴对称图形但不是中心对称图形的是（ ） A． B． C． D． 【解答】解：A、是轴对称图形但不是中心对称图形，故本选项正确； B、是轴对称图形，也是中心对称图形，故本选项错误； C、不是轴对称图形，是中心对称图形，故本选项错误； D、是轴对称图形，也是中心对称图形，故本选项错误． 故选：A． 9．若正多边形的一个内角是 150°，则该正多边形的边数是（ ） A．6 B．12 C．16 D．18 【解答】解：设多边形为 n 边形，由题意，得 （n﹣2）•180°＝150n， 解得 n＝12， 故选：B． 10．如图所示，用量角器度量∠AOB，可以读出∠AOB 的度数为（ ） 第 16页（共 34页） A．45° B．55° C．125° D．135° 【解答】解：由图形所示，∠AOB 的度数为 55°， 故选：B． 11．内角和为 540°的多边形是（ ） A． B． C． D． 【解答】解：设多边形的边数是 n，则 （n﹣2）•180°＝540°， 解得 n＝5． 故选：C． 12．如图是某个几何体的三视图，该几何体是（ ） A．圆锥 B．三棱锥 C．圆柱 D．三棱柱 【解答】解：根据主视图和左视图为矩形判断出是柱体，根据俯视图是三角形可判断出 这个几何体应该是三棱柱． 故选：D． 13．剪纸是我国传统的民间艺术，下列剪纸作品中，是轴对称图形的为（ ） 第 17页（共 34页） A． B． C． D． 【解答】解：A、不是轴对称图形， B、不是轴对称图形， C、不是轴对称图形， D、是轴对称图形， 故选：D． 14．如图，直线 l1，l2，l3 交于一点，直线 l4∥l1，若∠1＝124°，∠2＝88°，则∠3 的度 数为（ ） A．26° B．36° C．46° D．56° 【解答】解：如图，∵直线 l4∥l1， ∴∠1+∠AOB＝180°，而∠1＝124°， ∴∠AOB＝56°， ∴∠3＝180°﹣∠2﹣∠AOB ＝180°﹣88°﹣56° ＝36°， 故选：B． 第 18页（共 34页） 15．如图，公路 AC，BC 互相垂直，公路 AB 的中点 M 与点 C 被湖隔开．若测得 AM 的长 为 1.2km，则 M，C 两点间的距离为（ ） A．0.5km B．0.6km C．0.9km D．1.2km 【解答】解：∵在 Rt△ABC 中，∠ACB＝90°，M 为 AB 的中点， ∴MC＝ AB＝AM＝1.2km． 故选：D． 16．如图是几何体的三视图，该几何体是（ ） A．圆锥 B．圆柱 C．正三棱柱 D．正三棱锥 【解答】解：该几何体的左视图为矩形，俯视图亦为矩形，主视图是一个三角形， 则可得出该几何体为三棱柱． 故选：C． 17．如图， ⊙ O 的直径 AB 垂直于弦 CD，垂足为 E，∠A＝22.5°，OC＝4，CD 的长为 （ ） A．2 B．4 C．4 D．8 【解答】解：∵∠A＝22.5°， 第 19页（共 34页） ∴∠BOC＝2∠A＝45°， ∵ ⊙ O 的直径 AB 垂直于弦 CD， ∴CE＝DE，△OCE 为等腰直角三角形， ∴CE＝ OC＝2 ， ∴CD＝2CE＝4 ． 故选：C． 18．如图，直线 a，b 被直线 c 所截，a∥b，∠1＝∠2，若∠3＝40°，则∠4 等于（ ） A．40° B．50° C．70° D．80° 【解答】解：∵∠1＝∠2，∠3＝40°， ∴∠1＝ ×（180°﹣∠3）＝ ×（180°﹣40°）＝70°， ∵a∥b， ∴∠4＝∠1＝70°． 故选：C． 19．如图，为估算某河的宽度，在河对岸选定一个目标点 A，在近岸取点 B，C，D，使得 AB⊥BC，CD⊥BC，点 E 在 BC 上，并且点 A，E，D 在同一条直线上．若测得 BE＝20m， CE＝10m，CD＝20m，则河的宽度 AB 等于（ ） 第 20页（共 34页） A．60m B．40m C．30m D．20m 【解答】解：∵AB⊥BC，CD⊥BC， ∴△BAE∽△CDE， ∴ ∵BE＝20m，CE＝10m，CD＝20m， ∴ 解得：AB＝40， 故选：B． 20．下列图形中，是中心对称图形，但不是轴对称图形的是（ ） A． B． C． D． 【解答】解：A、不是轴对称图形，是中心对称图形．故此选项正确； B、是轴对称图形，也是中心对称图形．故此选项错误； C、是轴对称图形，不是中心对称图形．故此选项错误； D、是轴对称图形，不是中心对称图形．故此选项错误． 故选：A． 21．正十边形的每个外角等于（ ） A．18° B．36° C．45° D．60° 【解答】解：360°÷10＝36°， 所以，正十边形的每个外角等于 36°． 故选：B． 22．如图是某个几何体的三视图，该几何体是（ ） A．长方体 B．正方体 C．圆柱 D．三棱柱 【解答】解：根据主视图和左视图为矩形判断出是柱体，根据俯视图是三角形可判断出 这个几何体应该是三棱柱． 第 21页（共 34页） 故选：D． 23．如图，直线 AB，CD 交于点 O，射线 OM 平分∠AOC，若∠BOD＝76°，则∠BOM 等 于（ ） A．38° B．104° C．142° D．144° 【解答】解：∵∠BOD＝76°， ∴∠AOC＝∠BOD＝76°， ∵射线 OM 平分∠AOC， ∴∠AOM＝ ∠AOC＝ ×76°＝38°， ∴∠BOM＝180°﹣∠AOM＝180°﹣38°＝142°． 故选：C． 24．下列图形中，既是中心对称又是轴对称图形的是（ ） A．等边三角形 B．平行四边形 C．梯形 D．矩形 【解答】解：A、是轴对称图形，不是中心对称图形．故本选项错误； B、不是轴对称图形，是中心对称图形．故本选项错误； C、是轴对称图形，不是中心对称图形．故本选项错误； D、既是轴对称图形，又是中心对称图形．故本选项正确． 故选：D． 25．如图，在梯形 ABCD 中，AD∥BC，对角线 AC，BD 相交于点 O，若 AD＝1，BC＝3， 则 的值为（ ） A． B． C． D． 【解答】解：∵四边形 ABCD 是梯形， 第 22页（共 34页） ∴AD∥CB， ∴△AOD∽△COB， ∴ ， ∵AD＝1，BC＝3． ∴ ＝ ． 故选：B． 26．如图，在△ABC 中，点 D、E 分 AB、AC 边上，DE∥BC，若 AD：AB＝3：4，AE＝6， 则 AC 等于（ ） A．3 B．4 C．6 D．8 【解答】解：∵DE∥BC， ∴△ADE∽△ABC， ∴AD：AB＝AE：AC， 而 AD：AB＝3：4，AE＝6， ∴3：4＝6：AC， ∴AC＝8． 故选：D． 27．若菱形两条对角线的长分别为 6 和 8，则这个菱形的周长为（ ） A．20 B．16 C．12 D．10 【解答】解：如图，在菱形 ABCD 中，AC＝8，BD＝6． ∵ABCD 为菱形， ∴AC⊥BD，BO＝3，AO＝4． ∴AB＝5． ∴周长＝4×5＝20． 故选：A． 第 23页（共 34页） 28．一个几何体的三视图如图所示，这个几何体是（ ） A．棱柱 B．正方形 C．圆柱 D．圆锥 【解答】解：根据主视图和左视图为矩形可判断出该几何体是柱体， 根据俯视图是圆可判断出该几何体为圆柱． 故选：C． 29．若一个正多边形的一个外角是 40°，则这个正多边形的边数是（ ） A．10 B．9 C．8 D．6 【解答】解：多边形的每个外角相等，且其和为 360°， 据此可得 ＝40，解得 n＝9． 故选：B． 30．若一个多边形的内角和等于 720°，则这个多边形的边数是（ ） A．5 B．6 C．7 D．8 【解答】解：因为多边形的内角和公式为（n﹣2）•180°， 所以（n﹣2）×180°＝720°， 解得 n＝6， 所以这个多边形的边数是 6． 故选：B． 二．填空题（共 20 小题） 31．如图，已知△ABC，通过测量、计算得△ABC 的面积约为 1.9 cm2．（结果保留一位 小数） 第 24页（共 34页） 【解答】解：过点 C 作 CD⊥AB 的延长线于点 D，如图所示． 经过测量，AB＝2.2cm，CD＝1.7cm， ∴S△ABC＝ AB•CD＝ ×2.2×1.7≈1.9（cm2）． 故答案为：1.9． 32．在如图所示的几何体中，其三视图中有矩形的是 ①② ．（写出所有正确答案的序号） 【解答】解：长方体主视图，左视图，俯视图都是矩形， 圆柱体的主视图是矩形，左视图是矩形，俯视图是圆， 圆锥的主视图、左视图是等腰三角形，俯视图是带有圆心的圆， 故答案为： ①② ． 33．如图所示的网格是正方形网格，则∠PAB+∠PBA＝ 45 °（点 A，B，P 是网格线交 点）． 【解答】解：延长 AP 交格点于 D，连接 BD， 则 PD2＝BD2＝1+22＝5，PB2＝12+32＝10， ∴PD2+DB2＝PB2， ∴∠PDB＝90°， ∴∠DPB＝∠PAB+∠PBA＝45°， 故答案为：45． 第 25页（共 34页） 34．把图 1 中的菱形沿对角线分成四个全等的直角三角形，将这四个直角三角形分别拼成如 图 2，图 3 所示的正方形，则图 1 中菱形的面积为 12 ． 【解答】解：如图 1 所示： ∵四边形 ABCD 是菱形， ∴OA＝OC，OB＝OD，AC⊥BD， 设 OA＝x，OB＝y， 由题意得： ， 解得： ， ∴AC＝2OA＝6，BD＝2OB＝4， ∴菱形 ABCD 的面积＝ AC×BD＝ ×6×4＝12； 故答案为：12． 35．在矩形 ABCD 中，M，N，P，Q 分别为边 AB，BC，CD，DA 上的点（不与端点重合）， 对于任意矩形 ABCD，下面四个结论中， ① 存在无数个四边形 MNPQ 是平行四边形； ② 存在无数个四边形 MNPQ 是矩形； ③ 存在无数个四边形 MNPQ 是菱形； ④ 至少存在一个四边形 MNPQ 是正方形． 第 26页（共 34页） 所有正确结论的序号是 ①②③ ． 【解答】解： ① 如图，∵四边形 ABCD 是矩形，连接 AC，BD 交于 O， 过点 O 直线 MP 和 QN，分别交 AB，BC，CD，AD 于 M，N，P，Q， 则四边形 MNPQ 是平行四边形， 故当 MQ∥PN，PQ∥MN，四边形 MNPQ 是平行四边形， 故存在无数个四边形 MNPQ 是平行四边形；故正确； ② 如图，当 PM＝QN 时，四边形 MNPQ 是矩形，故存在无数个四边形 MNPQ 是矩形； 故正确； ③ 如图，当 PM⊥QN 时，存在无数个四边形 MNPQ 是菱形；故正确； ④ 当四边形 MNPQ 是正方形时，MQ＝PQ， 则△AMQ≌△DQP， ∴AM＝QD，AQ＝PD， ∵PD＝BM， ∴AB＝AD， ∴四边形 ABCD 是正方形与任意矩形 ABCD 矛盾，故错误； 故答案为： ①②③ ． 36．如图所示的网格是正方形网格，∠BAC ＞ ∠DAE．（填“＞”，“＝”或“＜”） 【解答】解：解法一：在 AD 上取一点 G，在网格上取点 F，构建△AFG 为等腰直角三 角形， 第 27页（共 34页） ∵tan∠BAC＝ ＝1，tan∠EAD＜1， ∴∠BAC＞∠EAD； 解法二：连接 NH，BC，过 N 作 NP⊥AD 于 P， S△ANH＝2×2﹣ ﹣ ×1×1＝ AH•NP， ＝ PN， PN＝ ， Rt△ANP 中，sin∠NAP＝ ＝ ＝ ＝0.6， Rt△ABC 中，sin∠BAC＝ ＝ ＝ ＞0.6， ∵正弦值随着角度的增大而增大， ∴∠BAC＞∠DAE， 故答案为：＞． 37．如图，点 A，B，C，D 在 ⊙ O 上， ＝ ，∠CAD＝30°，∠ACD＝50°，则∠ADB ＝ 70° ． 第 28页（共 34页） 【解答】解：∵ ＝ ，∠CAD＝30°， ∴∠CAD＝∠CAB＝30°， ∴∠DBC＝∠DAC＝30°， ∵∠ACD＝50°， ∴∠ABD＝50°， ∴∠ACB＝∠ADB＝180°﹣∠CAB﹣∠ABC＝180°﹣50°﹣30°﹣30°＝70°． 故答案为：70°． 38．如图，在矩形 ABCD 中，E 是边 AB 的中点，连接 DE 交对角线 AC 于点 F，若 AB＝4， AD＝3，则 CF 的长为 ． 【解答】解：∵四边形 ABCD 为矩形， ∴AB＝CD，AD＝BC，AB∥CD， ∴∠FAE＝∠FCD， 又∵∠AFE＝∠CFD， ∴△AFE∽△CFD， ∴ ＝ ＝2． ∵AC＝ ＝5， ∴CF＝ •AC＝ ×5＝ ． 故答案为： ． 第 29页（共 34页） 39．如图，在△ABC 中，M、N 分别为 AC，BC 的中点．若 S△CMN＝1，则 S 四边形 ABNM＝ 3 ． 【解答】解：∵M，N 分别是边 AC，BC 的中点， ∴MN 是△ABC 的中位线， ∴MN∥AB，且 MN＝ AB， ∴△CMN∽△CAB， ∴ ＝（ ）2＝ ， ∴ ＝ ， ∴S 四边形 ABNM＝3S△CMN＝3×1＝3． 故答案为：3． 40．如图，AB 为 ⊙ O 的直径，C、D 为 ⊙ O 上的点， ＝ ．若∠CAB＝40°，则∠CAD ＝ 25° ． 【解答】解：如图，连接 BC，BD， ∵AB 为 ⊙ O 的直径， ∴∠ACB＝90°， 第 30页（共 34页） ∵∠CAB＝40°， ∴∠ABC＝50°， ∵ ＝ ， ∴∠ABD＝∠CBD＝ ∠ABC＝25°， ∴∠CAD＝∠CBD＝25°． 故答案为：25°． 41．如图，在平面直角坐标系 xOy 中，△AOB 可以看作是△OCD 经过若干次图形的变化（平 移、轴对称、旋转）得到的，写出一种由△OCD 得到△AOB 的过程： △OCD 绕 C 点 顺时针旋转 90°，并向左平移 2 个单位得到△AOB ． 【解答】解：△OCD 绕 C 点顺时针旋转 90°，并向左平移 2 个单位得到△AOB（答案不 唯一）． 故答案为：△OCD 绕 C 点顺时针旋转 90°，并向左平移 2 个单位得到△AOB． 42．如图，小军、小珠之间的距离为 2.7m，他们在同一盏路灯下的影长分别为 1.8m，1.5m， 已知小军、小珠的身高分别为 1.8m，1.5m，则路灯的高为 3 m． 第 31页（共 34页） 【解答】解：如图，∵CD∥AB∥MN， ∴△ABE∽△CDE，△ABF∽△MNF， ∴ ， ， 即 ， ， 解得：AB＝3m． 答：路灯的高为 3m． 43．如图是由射线 AB，BC，CD，DE，EA 组成的平面图形，则∠1+∠2+∠3+∠4+∠5＝ 360 ° ． 【解答】解：∠1+∠2+∠3+∠4+∠5 ＝（180°﹣∠BAE）+（180°﹣∠ABC）+（180°﹣∠BCD）+（180°﹣∠CDE）+（180° ﹣∠DEA） ＝180°×5﹣（∠BAE+∠ABC+∠BCD+∠CDE+∠DEA） ＝900°﹣（5﹣2）×180° ＝900°﹣540° ＝360°． 故答案为：360°． 44．在某一时刻，测得一根高为 1.8m 的竹竿的影长为 3m，同时测得一根旗杆的影长为 25m， 第 32页（共 34页） 那么这根旗杆的高度为 15 m． 【解答】解：设旗杆高度为 x 米， 由题意得， ＝ ， 解得 x＝15． 故答案为：15． 45．如图，O 是矩形 ABCD 的对角线 AC 的中点，M 是 AD 的中点．若 AB＝5，AD＝12， 则四边形 ABOM 的周长为 20 ． 【解答】解：∵O 是矩形 ABCD 的对角线 AC 的中点，M 是 AD 的中点， ∴OM＝ CD＝ AB＝2.5， ∵AB＝5，AD＝12， ∴AC＝ ＝13， ∵O 是矩形 ABCD 的对角线 AC 的中点， ∴BO＝ AC＝6.5， ∴四边形 ABOM 的周长为 AB+AM+BO+OM＝5+6+6.5+2.5＝20， 故答案为：20． 46．如图，小明同学用自制的直角三角形纸板 DEF 测量树的高度 AB，他调整自己的位置， 设法使斜边 DF 保持水平，并且边 DE 与点 B 在同一直线上．已知纸板的两条直角边 DE ＝40cm，EF＝20cm，测得边 DF 离地面的高度 AC＝1.5m，CD＝8m，则树高 AB＝ 5.5 m． 【解答】解：∵∠DEF＝∠BCD＝90°∠D＝∠D 第 33页（共 34页） ∴△DEF∽△DCB ∴ ＝ ∵DE＝40cm＝0.4m，EF＝20cm＝0.2m，AC＝1.5m，CD＝8m， ∴ ＝ ∴BC＝4 米， ∴AB＝AC+BC＝1.5+4＝5.5 米， 故答案为：5.5． 47．若下图是某几何体的表面展开图，则这个几何体是 圆柱 ． 【解答】解：一个长方形和两个圆折叠后，能围成的几何体是圆柱． 故答案为：圆柱． 48．如图，AB 为圆 O 的直径，弦 CD⊥AB，垂足为点 E，连接 OC，若 OC＝5，CD＝8， 则 AE＝ 2 ． 【解答】解：∵AB 为圆 O 的直径，弦 CD⊥AB，垂足为点 E． ∴CE＝ CD＝4． 在直角△OCE 中，OE＝ ＝ ＝3． 则 AE＝OA﹣OE＝5﹣3＝2． 故答案为：2． 49．如图，AB 为 ⊙ O 的直径，弦 CD⊥AB，E 为 上一点，若∠CEA＝28°，则∠ABD＝ 28 度． 第 34页（共 34页） 【解答】解：由垂径定理可知 ，又根据在同圆或等圆中相等的弧所对的圆周角也 相等的性质可知∠ABD＝∠CEA＝28 度． 故答案为：28． 50．如图，正方形纸片 ABCD 的边长为 1，M、N 分别是 AD、BC 边上的点，将纸片的一角 沿过点 B 的直线折叠，使 A 落在 MN 上，落点记为 A′，折痕交 AD 于点 E，若 M、N 分别是 AD、BC 边的中点，则 A′N＝ ；若 M、N 分别是 AD、BC 边的上距 DC 最近的 n 等分点（n≥2，且 n 为整数），则 A′N＝ （n≥2，且 n 为整数） （用 含有 n 的式子表示）． 【解答】解：由题意得 BN＝ ，A′B＝1， 由勾股定理求得 ， 当 M，N 分别是 AD，BC 边的上距 DC 最近的 n 等分点（n≥2，且 n 为整数）， 即把 BC 分成 n 等份，BN 占（n﹣1）份， ∴BN＝ ，CN＝ ， 在 Rt△A′BN 中，根据勾股定理， （n≥2，且 n 为整数）． 声明：试 题解析著作权 属菁优网所有 ，未经书面同 意，不得复制 发布 日期：2020/1/19 8:59:28 ；用户： 金雨教育；邮 箱：309593466@qq.com ；学号： 335385