2017-2018学年广西柳州市柳江区九年级上期中考试数学试卷含答案 9页

‎2017-2018学年广西柳州市柳江区九年级（上）期中数学试卷 一、选择题（本大题共12小题，每小题3分，共36分）‎ ‎1．一元二次方程x（x﹣2）=0的解是（　　）‎ A．x=0 B．x1=﹣2 C．x1=0，x2=2 D．x=2‎ ‎2．下列图案中，不是中心对称图形的是（　　）‎ ‎3．抛物线y=﹣x2开口方向是（　　）‎ A．向上 B．向下 C．向左 D．向右 ‎4．用配方法解方程x2﹣2x﹣5=0时，原方程应变形为（　　）‎ A．（x+1）2=6 B．（x﹣1）2=6 C．（x+2）2=9 D．（x﹣2）2=9‎ ‎5．二次函数y=﹣2（x﹣1）2+3的图象的顶点坐标是（　　）‎ A．（1，3） B．（﹣1，3） C．（1，﹣3） D．（﹣1，﹣3）‎ ‎6．如图，四边形ABCD是正方形，△ADE绕着点A旋转90°后到达△ABF的位置，连接EF，则△AEF的形状是（　　）‎ A．等腰三角形 B．直角三角形 C．等腰直角三角形 D．等边三角形 ‎7．一元二次方程x2+2x+2=0的根的情况是（　　）‎ A．有两个相等的实数根 B．有两个不相等的实数根 C．只有一个实数根 D．无实数根 ‎8．若将抛物线y=x2向右平移2个单位，再向上平移3个单位，则所得抛物线的表达式为（　　）‎ A．y=（x+2）2+3 B．y=（x﹣2）2+3 C．y=（x+2）2﹣3 D．y=（x﹣2）2﹣3‎ ‎9．某校成立“情暖校园”爱心基金会，去年上半年发给每个经济困难的学生600元，今年上半年发给了800元，设每半年发给的资金金额的平均增长率为x，则下面列出的方程中正确的是（　　）‎ A．800（1﹣x）2=600 B．600（1﹣x）2=800 [来源:学科网ZXXK]‎ C．800（1+x）2=600 D．600（1+x）2=800‎ ‎10．设A（﹣2，y1），B（1，y2），C（2，y3）是抛物线y=﹣（x+1）2+1上的三点，‎ 则y1，y2，y3的大小关系为（　　）‎ A．y1＞y2＞y3 B．y1＞y3＞y2 C．y3＞y2＞y1 D．y3＞y1＞y2‎ ‎11．如图，△ABC中，将△ABC绕点A顺时针旋转40°后，得到△AB′C′，且C′在边BC上，则∠AC′C的度数为（　　）‎ A．50° B．60° C．70° D．80°‎ ‎12．二次函数y=ax2+bx+c的图象如图所示，则一次函数y=bx+a的图象不经过（　　）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 二、填空题（本大题共6小题，每小题3分，共18分）‎ ‎13．点（﹣2，1）关于原点对称的点的坐标为　 　．‎ ‎14．二次函数y=2（x﹣3）2﹣4的最小值为　 　．‎ ‎15．若x=2是一元二次方程x2+x﹣a=0的解，则a的值为　 　．‎ ‎16．若函数是二次函数，则m的值为　 　．‎ ‎17．已知方程5x2+kx﹣10=0的一个根是﹣5，则它的另一个根是　 　．‎ ‎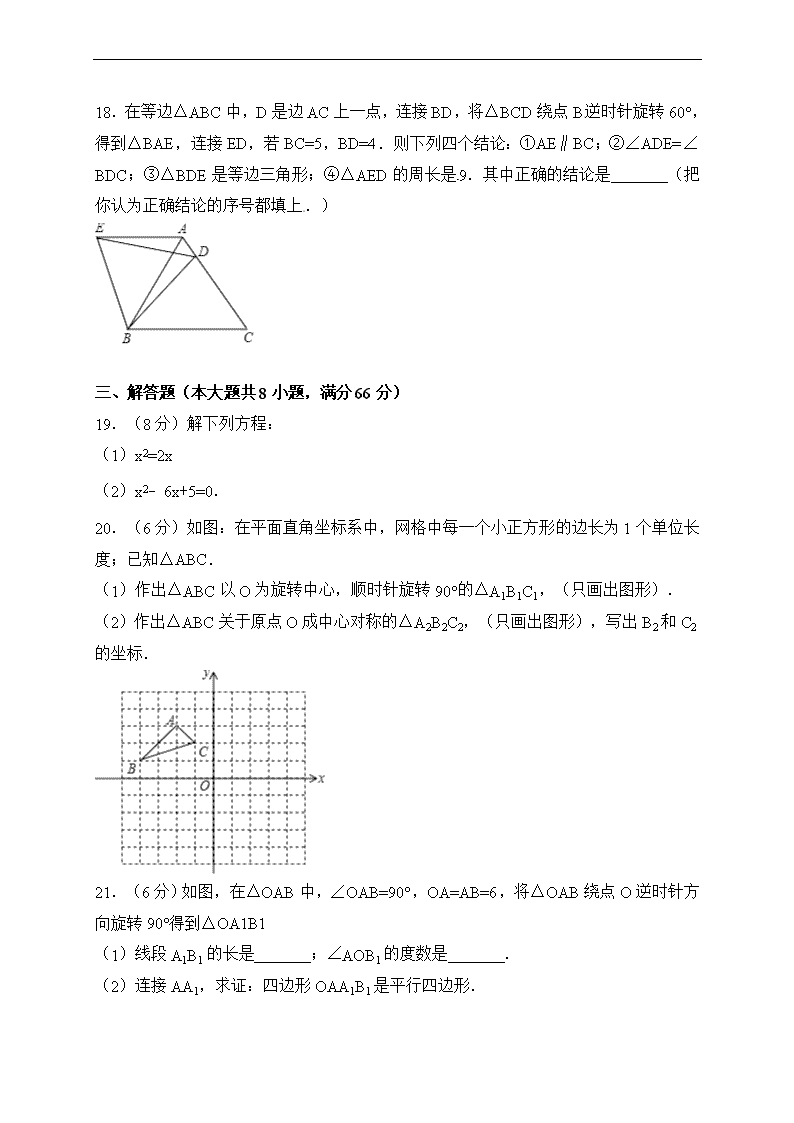18．在等边△ABC中，D是边AC上一点，连接BD，将△BCD绕点B逆时针旋转60°，得到△BAE，连接ED，若BC=5，BD=4．则下列四个结论：①AE∥BC；②∠ADE=∠BDC；③△BDE是等边三角形；④△AED的周长是9．其中正确的结论是　 　（把你认为正确结论的序号都填上．）‎ ‎　‎ 三、解答题（本大题共8小题，满分66分）‎ ‎19．（8分）解下列方程：‎ ‎（1）x2=2x ‎（2）x2﹣6x+5=0．‎ ‎20．（6分）如图：在平面直角坐标系中，网格中每一个小正方形的边长为1个单位长度；已知△ABC．‎ ‎（1）作出△ABC以O为旋转中心，顺时针旋转90°的△A1B1C1，（只画出图形）．‎ ‎（2）作出△ABC关于原点O成中心对称的△A2B2C2，（只画出图形），写出B2和C2的坐标．‎ ‎21．（6分）如图，在△OAB中，∠OAB=90°，OA=AB=6，将△OAB绕点O逆时针方向旋转90°得到△OA1B1‎ ‎（1）线段A1B1的长是　 　；∠AOB1的度数是　 　．‎ ‎（2）连接AA1，求证：四边形OAA1B1是平行四边形．‎ ‎22．（6分）已知函数图象如图所示，根据图象可得：‎ ‎（1）抛物线顶点坐标　 　；‎ ‎（2）对称轴为　 　；‎ ‎（3）当x=　 　时，y有最大值是　 　；‎ ‎（4）当　 　时，y随着x得增大而增大．‎ ‎（5）当　 　时，y＞0．‎ ‎23．（6分）如图，△ABC中，AB=AC=2，∠BAC=45°，△AEF是由△ABC绕点A按逆时针方向旋转得到的，连接BE、CF相交于点D，求证：BE=CF．‎ ‎24．（10分）已知抛物线的解析式为y=x2﹣（2m﹣1）x+m2﹣m ‎（1）求证：此抛物线与x轴必有两个不同的交点；‎ ‎（2）若此抛物线与直线y=x﹣3m+4的一个交点在y轴上，求m的值．‎ ‎25．（12分）某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利44元，为了扩大销售，增加盈利，尽快减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出5件．‎ ‎（1）若商场平均每天要盈利1600元，每件衬衫应降价多少元？‎ ‎（2）若该商场要每天盈利最大，每件衬衫应降价多少元？盈利最大是多少元？‎ ‎26．（12分）已知：二次函数y=x2+bx+c的图象与x轴交于A，B两点，其中A点坐标为（﹣3，0），与y轴交于点C，点D（﹣2，﹣3）在抛物线上．[来源:学§科§网]‎ ‎（1）求抛物线的解析式；‎ ‎（2）抛物线的对称轴上有一动点P，求出PA+PD的最小值；‎ ‎（3）若抛物线上有一动点P，使三角形ABP的面积为6，求P点坐标．‎ ‎　‎ ‎2017-2018学年广西柳州市柳江区九年级（上）期中数学试卷 数学答案 一、 选择题：‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ C C B B A C D[来源:学|科|网Z|X|X|K]‎ B D A C D 二、填空题：‎ ‎13. （2，-1） ， 14. -4 ， 15. 6 ， 16. -3 ，17. ， 18. ①③④‎ 二、 解答题 ‎19.解方程：⑴ ⑵x2－6x+5=0 [来源:Zxxk.Com]‎ 解: ---------1分 解: -------2分 ‎ ‎---------3分 或-------3分 ‎ 解得或-------4分 解得或 -------4分 ‎ ‎20.、（本题6分） ‎ B2(4,-1)------1分 ‎ C2(1,-2)-----1分 ‎ 每个图得2分 ‎21.（本题6分）解：（1）6，135°；---------2分（一空一分）） （2）∵∠A1OA=∠OA1B1=90°， ∴A1B1∥OA，---------3分 又∵OA=AB=A1B1---------4分 ∴四边形OAA1B1是平行四边形。---------6分[来源:学#科#网]‎ ‎-5‎ ‎-1‎ o y x ‎2‎ ‎22. （1）抛物线顶点坐标 （-3,2） ；---------1分 ‎（2）对称轴为 直线x=-3 ；---------2分 ‎（3）当x= -3 时，y有最大值是 2 ；---------4分 ‎（4）当x满足x＜-3 时，y随着x得增大而增大。-------5分 ‎（5）当x满足 -5＜x ＜-1 时，y＞0. ---------6分 ‎ ‎23.（1）证明：∵△AEF是由△ABC绕点A按逆时针方向旋转得到的，‎ ‎∴AE=AF=AB=AC=2，∠EAF=∠BAC=45°，‎ ‎∴∠BAC+∠3=∠EAF+∠3，即∠BAE=∠CAF，---------2分 在△ABE和△ACF中 ‎，‎ ‎∴△ABE≌△ACF，---------5分 ‎∴BE=CF；---------6分 ‎24.证明：（1）令y=0得：x2-（2m-1）x+m2-m=0①---------1分 ∵△=（2m-1）2-4（m2-m）×1=1＞0---------3分 ∴方程①有两个不等的实数根， ∴原抛物线与x轴有两个不同的交点---------4分 （2）令：x=0，根据题意有：m2-m=-3m+4---------6分 解得m=-1+或-1----------10分 （说明：少一个解扣2分）‎ ‎25.（1）解：设每件衬衫降价x元，可使每天盈利1600元，---------1分 ‎ 根据题意可列方程：(44-x)(20+5x)=1600---------3分 ‎ ‎ 整理，得 x²-40x+144=0 (x-36)(x-4)=0‎ ‎ 解得x=36或x=4---------5分 ‎ ‎ 因为尽快减少库存，取x=36---------6分 ‎ 答：每件衬衫降价36元更利于销售---------7分 ‎ ‎（2）解：设每件衬衫降价a元，可使每天盈利y元，---------8分 ‎ y=(44-a)(20+5a) ---------10分 ‎ ‎=-5 a²+200a+880‎ ‎=-5（a-20）²+2880---------11分 ‎-5＜0 所以当a=20时， y有最大值2880‎ 所以，当每件衬衫降价20元时盈利最大，最大盈利是2880元---------12分 ‎ ‎26. 解:(1)将A（-3,0）,D(-2，-3)的坐标代入y=x2+bx+c 得---------1分 解得： ---------2分 ∴y=x2+2x-3---------3分 ‎ ‎（2）由：y=x2+2x-3得： 对称轴为：直线x=-1， 令y=0，则：x2+2x-3=0， ∴：x1=-3，x2=1， ∴点B坐标为（1，0）， 而点A与点B关于直线x=-1对称， ∴连接BD与对称轴的交点即为所求的P点．---------4分 ‎ 过点D作DF⊥x轴于点F，则：DF=3，BF=1-（-2）=3， 在Rt△BDF中，BD=，---------5分 ∵PA=PB， ∴PA+PD=PB+PD=BD=，---------6分 即PA+PD的最小值为．---------7分 ‎ ‎（3）∵抛物线与x轴相交于A，B两点 ‎∴x2+2x-3=0‎ 解得x1=-3，x2=1，‎ ‎∴ A、B的坐标分别为（-3,0）和（1, 0）---------8分 ‎ ‎∴AB=4---------9分 ‎ 设P点的坐标为（x, x2+2x-3）‎ ‎∵S△ABP=6‎ ‎∴×=6‎ ‎∴=‎ ‎∴x2+2x-3 =3或x2+2x-3=-3‎ 解得，；，---------11分 ‎ ‎∴P点的坐标为，，，----12分 ‎