中考数学专题复习练习：中心对称和中心对称图形 7页

典型例题一 例01． 下列几组几何图形中，既是轴对称图形，又是中心对称图形，完全正确的一组是（ ）．‎ ‎ A．正方形、菱形、矩形、平行四边形 B．正三角形、正方形、菱形、矩形 ‎ C．正方形、矩形、菱形 D．平行四边形、正方形、等腰三角形 ‎ 分析 A中平行四边形不是轴对称图形，B中正三角形不是中心对称图形，D中平行四 边形不是轴对称图形．正选C．‎ ‎ 解答 本题主要考查轴对称和中心对称图形的判定，易错点是弄错图形的对称性，解题关键是要熟悉所学过的图形的对称性．‎ 典型例题二 例02．如图，已知：四边形ABCD关于O点成中心对称图形. ‎ 求证：四边形ABCD是平行四边形. ‎ 分析：因为四边形ABCD是中心对称图形，所以A点与C点，B点与D点是对称点. 所以线段AC过O点，线段BD也过O点，且两条线段都被O点平分，故四边形ABCD是平行四边形. ‎ 证明：连结AC、BD. ‎ ‎∵ 四边形ABCD关于O点成中心对称图形，‎ ‎∴ O点在AC上，也在BD上，并且 ‎∴ 四边形ABCD是平行四边形. ‎ 说明：要应用轴对称或中心对称解决问题，应该判断清楚图形的对称的特点，找到对称点. ‎ 典型例题三 例03．如图，已知：矩形ABCD和关于点A对称. ‎ 求证：四边形是菱形. ‎ 分析：根据题意知点B与关于点A对称，点D和点关于点A对称，又四边形ABCD和是矩形，由中心对称的性质及矩形的性质即可证明. ‎ 证明：∵矩形ABCD和关于点A成中心对称图形. ‎ ‎∴ ，（关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分）. ‎ ‎∴ 四边形是平行四边形. ‎ 又∵四边形ABCD是矩形，∴‎ ‎∴四边形是菱形. 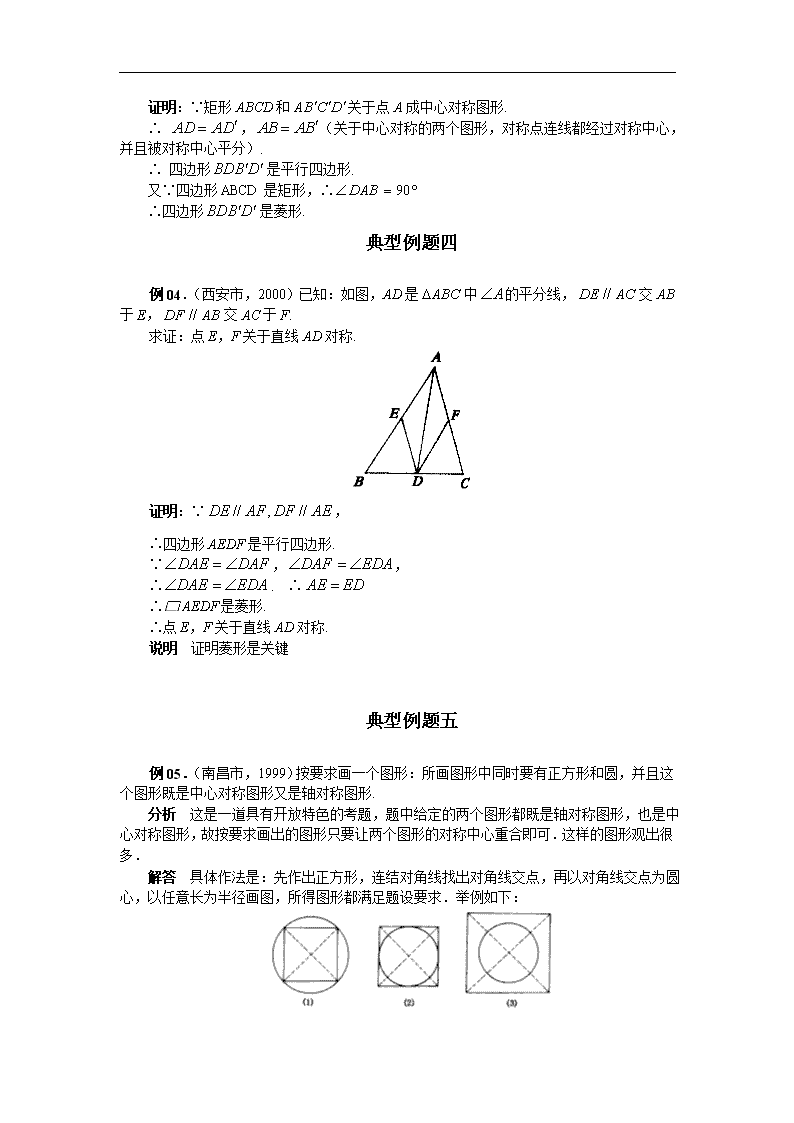‎ 典型例题四 例04．（西安市，2000）已知：如图，AD是中的平分线，交AB于E，交AC于F. ‎ 求证：点E，F关于直线AD对称. ‎ 证明：∵，‎ ‎∴四边形AEDF是平行四边形. ‎ ‎∵，，‎ ‎∴. ∴‎ ‎∴AEDF是菱形. ‎ ‎∴点E，F关于直线AD对称. ‎ 说明 证明菱形是关键 典型例题五 例05．（南昌市，1999）按要求画一个图形：所画图形中同时要有正方形和圆，并且这个图形既是中心对称图形又是轴对称图形. ‎ 分析 这是一道具有开放特色的考题，题中给定的两个图形都既是轴对称图形，也是中心对称图形，故按要求画出的图形只要让两个图形的对称中心重合即可．这样的图形观出很多．‎ 解答 具体作法是：先作出正方形，连结对角线找出对角线交点，再以对角线交点为圆心，以任意长为半径画图，所得图形都满足题设要求．举例如下：‎ 说明 本题考查轴对称图形和中心对称图形的应用，解题关键是要探索出两个图形的对称中心重合．‎ 选择题 ‎1．（四川省，2000）下列图形中，既是轴对称图形又是中心对称图形的是（ ）‎ A．角 B．等边三角形 C．线段 D．平行四边形 ‎2．下列多边形中，是中心对称图形而不是轴对称图形的是（ ）‎ A．平行四边形 B．矩形 C．菱形 D．正方形 ‎3．已知下列命题：（1）关于中心对称的两个图形一个不全等；（2）关于中心对称的两个图形是全等的图形；（3）两个全等的图形一定关于中心对称，其中真命题的个数是（ ）‎ A．0 B．1 C．2 D．3‎ ‎4．在平面上一个菱形绕它的中心旋转，使它与原来的菱形重合，那么旋转角度至少是（ ）‎ ‎ A． B． C． D．‎ ‎5．下列命题：（1）如果与关于中心对称，则；（2）如果，则与关于中心对称；（3）相交的两条直线是中心对称图形；（4）等边三角形是中心对称图形；（5）菱形是中心对称图形. 其中正确的命题的个数是（）‎ A．1 B．2 C．3 D．4‎ ‎6．（威海市，2001；北京市东城区，2002）下列四个图形中，既是轴对称图形又是中心对称图形的是（）‎ A．①②③④ B．①②③ C．①③ D．③‎ ‎7．下列图形中，是中心对称图形而不是轴对称图形的是（）．‎ ‎ A．平行四边形 B．矩形 C．菱形 D．正方形 ‎8．下列图形中，既是轴对称图形，又是中心对称图形的是（）．‎ ‎ A．等腰三角形 B．等边三角形 C．平行四边形 D．矩形 ‎9．下列说法中正确的是（）．‎ ‎ A．矩形的每一条对角线都是矩形的对称轴 ‎ B．平行四边形对角线的交点是平行四边形的对称中心 ‎ C．菱形是轴对称图形，但不是中心对称图形 ‎ D．中心对称图形就是中心对称 参考答案：‎ ‎1．C 2．A 3．B 4. A 5．C 6．D 7．A 8．D 9．B 填空题 ‎1．在平行四边形，菱形，等边三角形中，轴对称图形有_____种，中心对称图形有______种. ‎ ‎2．既是中心对称图形，又是轴对称图形，且只有两条对称轴的四边形是_______. ‎ ‎3．关于中心对称的两个图形，对应线段_______. ‎ ‎4．（徐州市，2000）在下面四个图形中，图形①与图形_______成轴对称；图形①与图形________成中心对称（填写符合要求的图形所对应的序号）‎ 参考答案：‎ ‎1．3，3 ‎ ‎2．矩形或菱形 ‎ ‎3．平行且相等 ‎4．④，③‎ 解答题 ‎1．如图，已知线段AB及AB外一点P，求作线段，使与AB关于点P对称. ‎ ‎2．如图，已知及点P，求作，使与关于点P对称. ‎ ‎3．如图，已知及其内部一点O，求作，使与关于点O对称. ‎ ‎4．如图，已知：矩形ABCD和矩形关于A点对称. ‎ 求证：四边形是菱形. ‎ ‎5．已知ABCD，作四边形，使它与已知平行四边形关于顶点A对称，并证明四边形是平行四边形. ‎ ‎6．如图，四边形ABCD关于O点成中心对称图形，‎ 求证：四边形ABCD是平行四边形. ‎ ‎7．（山西省，2000）如图，矩形ABCD是篮球场地简图，请你画图找出它们的对称中心O. ‎ ‎8．（南昌市，2001）如图，将标号为A、B、C、D的正方形沿图中的虚线剪开后得到标号为P、Q、M、N的四组图形. 试按照“哪个正方形剪开后得到哪组图形”的对应关系，填空：‎ A与______对应；B与______对应；C与______对应；D与______对应. ‎ ‎9．（遵义市，2000）如图，请画出把下列矩形的面积两等分的直线，并填空. （一个矩形只画一条直线，不写画法）‎ 在一个矩形中，把此矩形面积两等分的直线最多有______条，这些直线都必须经过该矩形______点. ‎ ‎10．（聊城市，2000）如图，已知矩形ABCD中，，，将矩形折叠使C点与A点重合. ‎ ‎（1）作出折痕EF，并写出作法（E点在BC边上，F点在AD边上）；‎ ‎（2）翻折后点D落在上，求此时B、之间的距离. ‎ ‎11．（济南市，2001）如图是未完成的上海大众汽车的标志图案. 该图案应该是以直线为对称轴的轴对称图形，现已完成对称轴左边的部分，请你补全标志图案，画出对称轴右边的部分（要求用尺规作图，保留痕迹，不写作法）. ‎ ‎12．（荆州市，2002）有一块方角形钢板如图所示，请你用一条直线将其分为面积相等的两部分（不写作法，保留作图痕迹，在图中直接画出）. ‎ ‎13．（盐城市，2002）已知：如图，矩形ABCD. ‎ ‎（1）作出点C关于BD所在直线的对称点（用尺规作图，不写作法，保留作图痕迹）‎ ‎（2）连结，，若与重叠部分的面积等于面积的，求的度数. ‎ ‎14．（福州市，2002）已知：图（1），图（2）分别是正方形网格上的两个轴对称图形（阴影部分），其面积分别为，（网格中最小的正方形面积为一个平方单位），请观察图形并解答下列问题. ‎ ‎（1）填空：的值是_______；‎ ‎（2）请在图（3）的网格上画出一个面积为8个平方单位的中心对称图形. ‎ 参考答案：‎ ‎1．略 2．略 3．略 ‎4．因矩形ABCD和矩形关于A点对称，∴ ， ∴ 四边形是平行四边形. ∵ ，∴是菱形 ‎ ‎5． 图略，证法同第4题. ‎ ‎6．证明：连结AC，BD. ‎ ‎∵ 四边形ABCD关于O点成中心对称图形，‎ ‎∴ O点在AC和BD上，且. ‎ ‎∴ 四边形ABCD是平行四边形. ‎ ‎7．连结AC，BD交于O ‎ ‎8．M，P，Q，N ‎ ‎9．略 10．略 11．图略 12．略 ‎13．（1）略；（2）连结，，设与AD相交于E. 证，求得，∴ ‎ ‎14．（1）；（2）略