2009中考数学分类汇编-二次函数 43页

一、选择题 ‎1、（2009年台湾）向上发射一枚炮弹，经x秒后的高度为y公尺，且时间与高度关系为y=ax2+bx。若此炮弹在第7秒与第14秒时的高度相等，则再下列哪一个时间的高度是最高的？‎ ‎ (A) 第8秒 (B) 第10秒 (C) 第12秒 (D) 第15秒 。‎ ‎2、（2009年泸州）在平面直角坐标系中，将二次函数的图象向上平移2个单位，所得图象的解析式为 A． B． ‎ C． D．‎ ‎3、 (2009年四川省内江市)抛物线的顶点坐标是（ ）‎ A．（2，3） B．（－2，3） C．（2，－3） D．（－2，－3）‎ ‎5、（2009年桂林市、百色市）二次函数的最小值是（ ）．‎ ‎ A．2 B．‎1 C．－3 D． ‎ ‎6、(2009年上海市)抛物线（是常数）的顶点坐标是（ ）‎ A． B． C． D．‎ ‎7、(2009年陕西省)根据下表中的二次函数的自变量x与函数y的对应值，可判断二次函数的图像与x轴 【 】‎ x ‎…‎ ‎－1‎ ‎0‎ ‎1‎ ‎2‎ ‎…‎ y ‎…‎ ‎－1‎ ‎－2‎ ‎…‎ A．只有一个交点 ‎ B．有两个交点，且它们分别在y轴两侧 C．有两个交点，且它们均在y轴同侧 D．无交点 ‎8、（2009威海）二次函数的图象的顶点坐标是（　　）‎ A． B． C． D．‎ ‎9、（2009湖北省荆门市）函数y=ax＋1与y=ax2＋bx＋1（a≠0）的图象可能是（ ）‎ A． 　B． C． 　　　　D．‎ 解析：本题考查函数图象与性质，当时，直线从左向右是上升的，抛物线开口向上，D是错的，函数y=ax＋1与y=ax2＋bx＋1（a≠0）的图象必过（0，1），所以C是正确的，故选C．‎ ‎10、（2009年贵州黔东南州）抛物线的图象如图所示，根据图象可知，抛物线的解析式可能是（ ）‎ A、y=x2-x-2 B、y= ‎ C、y= D、y=‎ ‎11、（2009年齐齐哈尔市）已知二次函数的图象如图所示，则下列结论：；方程的两根之和大于0；随的增大而增大；④，其中正确的个数（）‎ A．4个 B．3个 C．2个 D．1个 x y O ‎1‎ ‎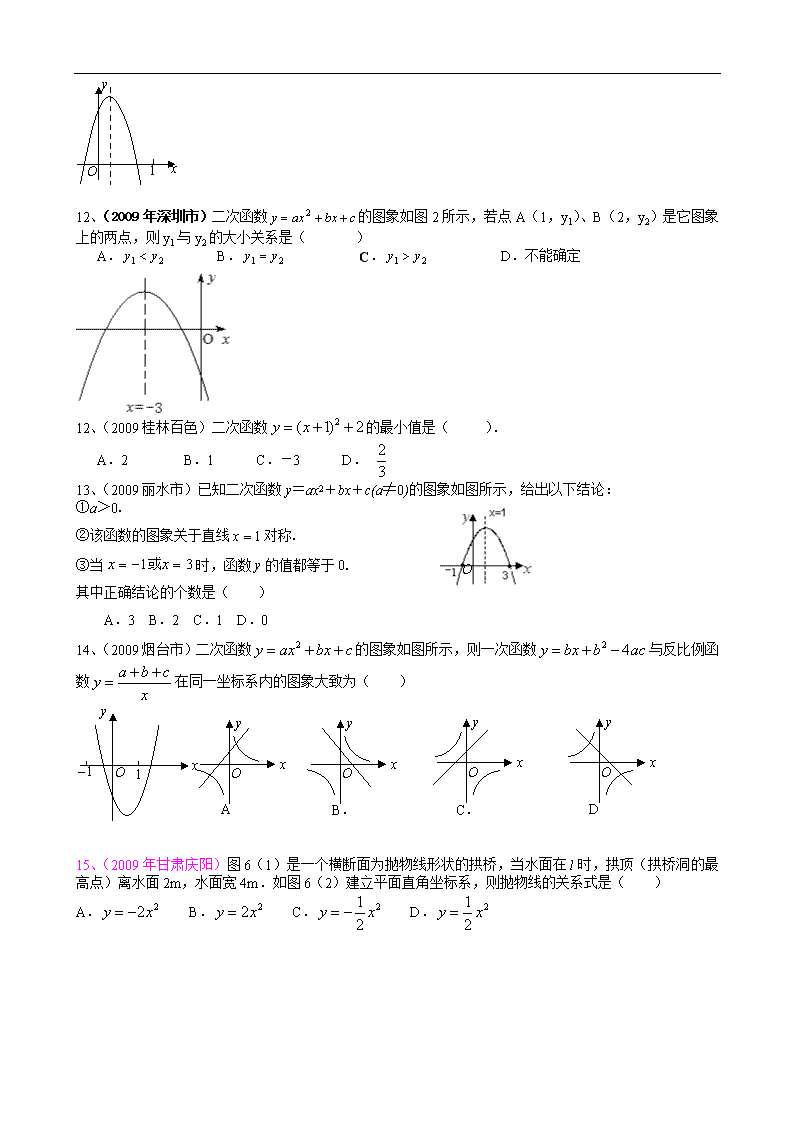12、（2009年深圳市）二次函数的图象如图2所示，若点A（1，y1）、B（2，y2）是它图象上的两点，则y1与y2的大小关系是（ ）‎ A． B． C． D．不能确定 ‎12、（2009桂林百色）二次函数的最小值是（ ）．‎ ‎ A．2 B．‎1 C．－3 D． ‎ ‎13、（2009丽水市）已知二次函数y＝ax2＋bx＋c(a≠0)的图象如图所示，给出以下结论：‎ O ‎①a＞0.‎ ‎②该函数的图象关于直线对称. ‎ ‎③当时，函数y的值都等于0.‎ 其中正确结论的个数是（ ）‎ ‎ A．3 B．‎2 C．1 D．0‎ ‎14、（2009烟台市）二次函数的图象如图所示，则一次函数与反比例函数在同一坐标系内的图象大致为（ ）‎ y x O y x O B．‎ C．‎ y x O A．‎ y x O D．‎ ‎1‎ O x y ‎15、（2009年甘肃庆阳）图6（1）是一个横断面为抛物线形状的拱桥，当水面在l时，拱顶（拱桥洞的最高点）离水面2m，水面宽4m．如图6（2）建立平面直角坐标系，则抛物线的关系式是（　　）‎ A． B． C． D．‎ 图6（1） 图6（2）‎ ‎16、（2009年甘肃庆阳）将抛物线向下平移1个单位，得到的抛物线是（　　）‎ A． B． C． D．‎ ‎17、（2009年广西南宁）已知二次函数（）的图象如图4所示，有下列四个结论：④，其中正确的个数有（ ）‎ A．1个 B．2个 C．3个 D．4个 ‎1‎ 图4‎ O x y ‎3‎ ‎18、(2009年鄂州)已知=次函数y＝ax+bx+c的图象如图．则下列5个代数式：ac，a+b+c，‎4a－2b+c，‎ ‎2a‎+b，‎2a－b中，其值大于0的个数为（ ）‎ ‎ A．2 B ‎3 ‎ C、4 D、5‎ ‎19、（2009年孝感）将函数的图象向右平移a个单位，得到函数的图象，则a的值为 A．1 B．‎2 ‎C．3 D．4 ‎ ‎20、（2009泰安）抛物线的顶点坐标为 ‎（A）（-2，7） （B）（-2，-25） （C）（2，7） （D）（2，-9）‎ ‎21、（2009年烟台市）二次函数的图象如图所示，则一次函数与反比例函数在同一坐标系内的图象大致为（ ）‎ ‎1‎ O x y y x O y x O B．‎ C．‎ y x O A．‎ y x O D．‎ ‎22、（2009年嘉兴市）已知，在同一直角坐标系中，函数与的图象有可能是（　▲　）‎ A．‎ B．‎ C．‎ D．‎ ‎23、（2009年新疆）如图，直角坐标系中，两条抛物线有相同的对称轴，下列关系不正确的是（ ）‎ A． B． C． D．‎ ‎24、（2009年天津市）在平面直角坐标系中，先将抛物线关于轴作轴对称变换，再将所得的抛物线关于轴作轴对称变换，那么经两次变换后所得的新抛物线的解析式为（ ）‎ A．　　B． C．　　D．‎ ‎25、（2009年南宁市）已知二次函数（）的图象如图所示，有下列四个结论：④，其中正确的个数有（ ）‎ A．1个 B．2个 C．3个 D．4个 ‎26、（2009年衢州）二次函数的图象上最低点的坐标是 A．(-1，-2) 　B．(1，-2) 　　C．(-1，2) 　D．(1，2)‎ ‎27、（2009年舟山）二次函数的图象上最低点的坐标是 A．(-1，-2) 　B．(1，-2) 　　C．(-1，2) 　D．(1，2)‎ ‎28、（2009年广州市）二次函数的最小值是（ ）‎ A.2 （B）1 （C）-1 （D）-2‎ ‎29、（2009年济宁市）小强从如图所示的二次函数的图象中，观察得出了下面五条信息：（1）；（2） ；（3）；（4） ； （5）. 你认为其中正确信息的个数有 A．2个 B．3个 C．4个 D．5个 ‎（第12题）‎ ‎30、（2009年广西钦州）将抛物线y＝2x2向上平移3个单位得到的抛物线的解析式是（ ）‎ ‎ A．y＝2x2＋3 B．y＝2x2－3‎ ‎ C．y＝2（x＋3）2 D．y＝2（x－3）2‎ ‎31、(2009宁夏)二次函数的图象如图所示，对称轴是直线，则下列四个结论错误的是（ ）D A． B．‎ C． D．‎ ‎1‎ ‎1‎ O x y ‎（8题图）‎ ‎32、(2009年南充)抛物线的对称轴是直线（ ）‎ A． B． C． D．‎ ‎33、(2009年湖州)已知图中的每个小方格都是边长为1的小正方形，每个小正方形的顶点称为格点，请你在图中任意画一条抛物线，问所画的抛物线最多能经过81个格点中的多少个？（ ）‎ A．6 B．‎7 ‎ C．8 D．9‎ ‎34、（2009年兰州）在同一直角坐标系中，函数和函数（是常数，且）的图象可能是 ‎35、（2009年兰州）把抛物线向左平移1个单位，然后向上平移3个单位，则平移后抛物线的解析式为 A． B．‎ C． D．‎ ‎36、（2009年兰州）二次函数的图象如图6所示，则下列关系式不正确的是 A．＜0 B.＞0 ‎ ‎ ‎ C.＞0 D.＞0‎ ‎ ‎ ‎37、（2009年遂宁）把二次函数用配方法化成的形式 ‎ A. B. ‎ C. D. ‎ ‎39、（2009年广州市）二次函数的最小值是（ ）‎ A.2 （B）1 （C）-1 （D）-2‎ ‎【关键词】二次函数 ‎41、（2009年台湾）向上发射一枚炮弹，经x秒后的高度为y公尺，且时间与高度关系为y=ax2+bx。若此炮弹在第7秒与第14秒时的高度相等，则再下列哪一个时间的高度是最高的？‎ ‎ (A) 第8秒 (B) 第10秒 (C) 第12秒 (D) 第15秒 。‎ ‎【关键词】二次函数极值 ‎【答案】B ‎43、（2009年湖北荆州）抛物线的对称轴是（ ）‎ A． B． ‎ C． D． ‎ ‎44、（2009年新疆乌鲁木齐市）要得到二次函数的图象，需将的图象（ ）．‎ A．向左平移2个单位，再向下平移2个单位 B．向右平移2个单位，再向上平移2个单位 C．向左平移1个单位，再向上平移1个单位 D．向右平移1个单位，再向下平移1个单位 ‎【‎ ‎45、（2009年黄石市）已知二次函数的图象如图所示，有以下结论：①；②；③；④；⑤其中所有正确结论的序号是（ ）‎ A．①② B． ①③④ ‎ C．①②③⑤ D．①②③④⑤‎ ‎1‎ ‎1‎ O x y ‎46、（2009 黑龙江大兴安岭）二次函数的图象如图，下列判断错误的是 （ ）‎ A． B． C． D．‎ ‎47、（2009年枣庄市）第11题图 ‎ y x O ‎1‎ ‎－1‎ 二次函数的图象如图所示，则下列关系式中错误的是（ ）‎ A．a＜0 ‎ B．c＞0‎ C．＞0‎ D．＞0‎ ‎【关键词】二次函数（a≠0）与a，b，c的关系 ‎【答案】D 二、填空题 ‎1、（2009年北京市）若把代数式化为的形式，其中为常数，则= .‎ ‎2、（2009年安徽）已知二次函数的图象经过原点及点（，），且图象与x轴的另一交点到原 点的距离为1，则该二次函数的解析式为 ‎ ‎3、已知二次函数的图象经过原点及点（，），且图象与x轴的另一交点到原点的距离为1，则该二次函数的解析式为 ．‎ ‎4、（2009年郴州市）抛物线的顶点坐标为__________．‎ ‎5、(2009年上海市)12．将抛物线向上平移一个单位后，得以新的抛物线，那么新的抛物线的表达式是 ．‎ ‎6、（2009年内蒙古包头）已知二次函数的图象与轴交于点、，且，与轴的正半轴的交点在的下方．下列结论：①；②；③；④．其中正确结论的个数是 个．‎ ‎7、（2009襄樊市）抛物线的图象如图6所示，则此抛物线的解析式为 ．‎ y x O ‎3‎ x=1‎ 图6‎ ‎8、（2009湖北省荆门市）函数取得最大值时，______．‎ ‎9、（2009年淄博市） 请写出符合以下三个条件的一个函数的解析式 ．‎ ‎①过点；‎ ‎②当时，y随x的增大而减小；‎ ‎③当自变量的值为2时，函数值小于2．‎ ‎10、（2009年贵州省黔东南州）二次函数的图象关于原点O（0, 0）对称的图象的解析式是_________________。‎ ‎11、（2009年齐齐哈尔市）当_____________时，二次函数有最小值．‎ ‎12、（2009年娄底）如图7，⊙O的半径为2，C1是函数y=x2的图象，C2是函数y=-x2的图象，则阴影部分的面积是 . ‎13、（2009年甘肃庆阳）图12为二次函数的图象，给出下列说法：‎ ‎①；②方程的根为；③；④当时，y随x 值的增大而增大；⑤当时，．‎ 其中，正确的说法有 ．（请写出所有正确说法的序号）‎ ‎14、(2009年鄂州)把抛物线y＝ax+bx+c的图象先向右平移3个单位，再向下平移2个单位，所得的图象的解析式是y＝x－3x+5，则a+b+c=__________‎ ‎15、（2009白银市）抛物线的部分图象如图8所示，请写出与其关系式、图象相关的2个正确结论：　　　　　　　　　，　　　　　　　　　　．（对称轴方程，图象与x正半轴、y轴交点坐标例外）‎ ‎16、(2009年甘肃定西)抛物线的部分图象如图8所示，请写出与其关系式、图象相关的2个正确结论：　　　　　　　　　，　　　　　　　　　　．（对称轴方程，图象与x正半轴、y轴交点坐标例外）‎ ‎17、（2009年包头）将一条长为20cm的铁丝剪成两段，并以每一段铁丝的长度为周长各做成一个正方形，则这两个正方形面积之和的最小值 是 cm2．‎ ‎18、（2009年包头）已知二次函数的图象与轴交于点、，且，与轴的正半轴的交点在的下方．下列结论：①；②；③；④．其中正确结论的个数是 个．‎ ‎19、（2009年莆田）出售某种文具盒，若每个获利元，一天可售出个，则当 元时，一天出售该种文具盒的总利润最大．‎ ‎20、(2009年本溪)如图所示，抛物线（）与轴的两个交点分别为和，当时，的取值范围是 ． ‎ ‎【‎ ‎21．(2009年湖州)已知抛物线（＞0）的对称轴为直线，且经过点试比较和的大小： _（填“>”，“<”或“=”）‎ ‎22、（2009年兰州）二次函数的图象如图12所示，点位于坐标原点， 点，，，…， 在y轴的正半轴上，点，，‎ ‎，…， 在二次函数位于第一象限的图象上， ‎ 若△,△，△，…，△‎ 都为等边三角形，则△的边长＝ . ‎ ‎23、（2009年北京市）若把代数式化为的形式，其中为常数，则= .‎ ‎24．(2009年咸宁市)已知、是抛物线上位置不同的两点，且关于抛物线的对称轴对称，则点、的坐标可能是_____________．（写出一对即可）‎ ‎25、（2009年安徽）已知二次函数的图象经过原点及点（，），且图象与x轴的另一交点到原 点的距离为1，则该二次函数的解析式为 ．‎ ‎26、（2009年黄石市）若抛物线与的两交点关于原点对称，则分别为 ．‎ ‎27、（2009 黑龙江大兴安岭）当 时，二次函数有最小值．‎ ‎ ‎ 三、解答题 ‎1、（2009年株洲市）如图1，中，，，点在线段上运动，点、分别在线段、上，且使得四边形是矩形．设的长为，矩形的面积为，已知是的函数，其图象是过点（12，36）的抛物线的一部分（如图2所示）．‎ ‎（1）求的长；‎ ‎（2）当为何值时，矩形的面积最大，并求出最大值．‎ 为了解决这个问题，孔明和研究性学习小组的同学作了如下讨论： ‎ 张明：图2中的抛物线过点（12，36）在图1中表示什么呢？‎ 李明：因为抛物线上的点是表示图1中的长与矩形面积的对应关系，那么，（12，36）表示当时，的长与矩形面积的对应关系.‎ 赵明：对，我知道纵坐标36是什么意思了！‎ 孔明：哦，这样就可以算出，这个问题就可以解决了.‎ ‎ 请根据上述对话，帮他们解答这个问题.‎ O ‎ ‎ 图1 图2‎ ‎2、（2009年株洲市）已知为直角三角形，，,点、在轴上，点坐标为（，）（），线段与轴相交于点，以（1，0）为顶点的抛物线过点、．‎ ‎（1）求点的坐标（用表示）；‎ ‎（2）求抛物线的解析式；‎ ‎ ‎ ‎ ‎ ‎（3）设点为抛物线上点至点之间的一动点，连结并延长交于点，连结 并延长交于点，试证明：为定值．‎ ‎3、（2009年重庆市江津区）某商场在销售旺季临近时 ，某品牌的童装销售价格呈上升趋势，假如这种童装开始时的售价为每件20元，并且每周（7天）涨价2元，从第6周开始，保持每件30元的稳定价格销售，直到11周结束，该童装不再销售。‎ ‎ （1）请建立销售价格y（元）与周次x之间的函数关系；‎ ‎ （2）若该品牌童装于进货当周售完，且这种童装每件进价z（元）与周次x之间的关系为， 1≤ x ≤11，且x为整数，那么该品牌童装在第几周售出后，每件获得利润最大？并求最大利润为多少？‎ ‎4、（2009年重庆市江津区）如图，抛物线与x轴交与A(1,0),B(- 3，0)两点，‎ ‎ （1）求该抛物线的解析式；‎ ‎（2）设（1）中的抛物线交y轴与C点，在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由.‎ ‎（3）在（1）中的抛物线上的第二象限上是否存在一点P，使△PBC的面积最大？，若存在，求出点P的坐标及△PBC的面积最大值.若没有，请说明理由.‎ 第26题图 ‎5、（2009年滨州）某商品的进价为每件40元．当售价为每件60元时，每星期可卖出300件，现需降价处理，且经市场调查：每降价1元，每星期可多卖出20件．在确保盈利的前提下，解答下列问题：‎ ‎（1）若设每件降价元、每星期售出商品的利润为元，请写出与的函数关系式，并求出自变量的取值范围；‎ ‎（2）当降价多少元时，每星期的利润最大？最大利润是多少？‎ ‎（3）请画出上述函数的大致图象．‎ ‎6、（2009年滨州） 如图①，某产品标志的截面图形由一个等腰梯形和抛物线的一部分组成，在等腰梯形中，，．对于抛物线部分，其顶点为的中点，且过两点，开口终端的连线平行且等于．‎ ‎（1）如图①所示，在以点为原点，直线为轴的坐标系内，点的坐标为，‎ 试求两点的坐标；‎ ‎（2）求标志的高度（即标志的最高点到梯形下底所在直线的距离）；‎ N B C D A M y x ‎（第4题图①）‎ ‎）‎ O A B C D ‎（第4题图②）‎ ‎））‎ ‎）‎ ‎20cm ‎30cm ‎45°‎ ‎（3）现根据实际情况，需在标志截面图形的梯形部分的外围均匀镀上一层厚度为‎3cm的保护膜，如图②，请在图中补充完整镀膜部分的示意图，并求出镀膜的外围周长．‎ ‎7、 (2009年四川省内江市)如图所示，已知点A（－1，0），B（3，0），C（0，t），且t＞0，tan∠BAC=3，抛物线经过A、B、C三点，点P（2，m）是抛物线与直线的一个交点。‎ ‎（1）求抛物线的解析式；‎ ‎（2）对于动点Q（1，n），求PQ+QB的最小值；‎ ‎（3）若动点M在直线上方的抛物线上运动，‎ 求△AMP的边AP上的高h的最大值。‎ ‎8、（2009仙桃）如图，已知抛物线y＝x2＋bx＋c经过矩形ABCD的两个顶点A、B，AB平行于x轴，对角线BD与抛物线交于点P，点A的坐标为(0，2)，AB＝4．‎ ‎(1)求抛物线的解析式；‎ ‎(2)若S△APO＝，求矩形ABCD的面积．‎ y x D N M Q B C O P E A ‎9、（2009年长春）如图，直线分别与轴、轴交于两点，直线与交于点，与过点且平行于轴的直线交于点．点从点出发，以每秒1个单位的速度沿轴向左运动．过点作轴的垂线，分别交直线于两点，以为边向右作正方形，设正方形与重叠部分（阴影部分）的面积为（平方单位）．点的运动时间为（秒）．‎ ‎（1）求点的坐标．（1分）‎ ‎（2）当时，求与之间的函数关系式．（4分）‎ ‎（3）求（2）中的最大值．（2分）‎ ‎（4）当时，直接写出点在正方形内部时的取值范围．（3分）‎ ‎10、（2009年郴州市） 如图11，已知正比例函数和反比例函数的图像都经过点M（－2，），且P（，－2）为双曲线上的一点，Q为坐标平面上一动点，PA垂直于x轴，QB垂直于y轴，垂足分别是A、B． ‎ ‎（1）写出正比例函数和反比例函数的关系式；‎ ‎（2）当点Q在直线MO上运动时，直线MO上是否存在这样的点Q，使得△OBQ与△OAP面积相等？如果存在，请求出点的坐标，如果不存在，请说明理由； ‎ ‎（3）如图12，当点Q在第一象限中的双曲线上运动时，作以OP、OQ为邻边的平行四边形OPCQ，求平行四边形OPCQ周长的最小值．‎ 图12‎ 图11‎ ‎10、（2009年常德市）已知二次函数过点A （0，），B（，0），C（）．‎ ‎ （1）求此二次函数的解析式；‎ ‎ （2）判断点M（1，）是否在直线AC上？‎ 图8‎ ‎ （3）过点M（1，）作一条直线与二次函数的图象交于E、F两点（不同于A，B，C三点），请自已给出E点的坐标，并证明△BEF是直角三角形．‎ ‎11、(2009年陕西省) 如图，在平面直角坐标系中，OB⊥OA，且OB＝2OA，点A的坐标是(－1，2)．‎ ‎（1）求点B的坐标；‎ ‎（2）求过点A、O、B的抛物线的表达式；‎ ‎（3）连接AB，在（2）中的抛物线上求出点P，使得S△ABP＝S△ABO．‎ ‎12、(2009年黄冈市)新星电子科技公司积极应对2008年世界金融危机，及时调整投资方向，瞄准光伏产业，建成了太阳能光伏电池生产线．由于新产品开发初期成本高，且市场占有率不高等因素的影响，产品投产上市一年来，公司经历了由初期的亏损到后来逐步盈利的过程（公司对经营的盈亏情况每月最后一天结算1次）．公司累积获得的利润y（万元）与销售时间第x（月）之间的函数关系式（即前x个月的利润总和y与x之间的关系）对应的点都在如图所示的图象上．该图象从左至右，依次是线段OA、曲线AB和曲线BC，其中曲线AB为抛物线的一部分，点A为该抛物线的顶点，曲线BC为另一抛物线的一部分，且点A，B，C的横坐标分别为4，10，12‎ ‎（1）求该公司累积获得的利润y（万元）与时间第x（月）之间的函数关系式；‎ ‎（2）直接写出第x个月所获得S（万元）与时间x（月）之间的函数关系式（不需要写出计算过程）；‎ ‎（3）前12个月中，第几个月该公司所获得的利润最多？最多利润是多少万元？‎ ‎13、(2009武汉)某商品的进价为每件40元，售价为每件50元，每个月可卖出210件；如果每件商品的售价每上涨1元，则每个月少卖10件（每件售价不能高于65元）．设每件商品的售价上涨元（为正整数），每个月的销售利润为元．‎ ‎（1）求与的函数关系式并直接写出自变量的取值范围；‎ ‎（2）每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？‎ ‎（3）每件商品的售价定为多少元时，每个月的利润恰为2200元？根据以上结论，请你直接写出售价在什么范围时，每个月的利润不低于2200元？‎ ‎14、(2009武汉)如图，抛物线经过、两点，与轴交于另一点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）已知点在第一象限的抛物线上，求点关于直线对称的点的坐标；‎ ‎（3）在（2）的条件下，连接，点为抛物线上一点，且，求点的坐标．‎ y x O A B C ‎15、(2009年安顺)如图，已知抛物线与交于A(－1，0)、E(3，0)两点，与轴交于点B(0，3)。‎ （1） 求抛物线的解析式；‎ （2） 设抛物线顶点为D，求四边形AEDB的面积；‎ （3） ‎△AOB与△DBE是否相似？如果相似，请给以证明；如果不相似，请说明理由。‎ ‎16、（2009重庆綦江）如图，已知抛物线经过点，抛物线的顶点为，过作射线．过顶点平行于轴的直线交射线于点，在轴正半轴上，连结．‎ ‎（1）求该抛物线的解析式；‎ ‎（2）若动点从点出发，以每秒1个长度单位的速度沿射线运动，设点运动的时间为．问当为何值时，四边形分别为平行四边形？直角梯形？等腰梯形？‎ x y M C D P Q O A B ‎（3）若，动点和动点分别从点和点同时出发，分别以每秒1个长度单位和2个长度单位的速度沿和运动，当其中一个点停止运动时另一个点也随之停止运动．设它们的运动的时间为，连接，当为何值时，四边形的面积最小？并求出最小值及此时的长．‎ ‎17、（2009威海）O A B C l y x 如图，在直角坐标系中，点A,B,C的坐标分别为（-1，0），（3，0）。（0，3），过A,B,C三点的抛物线的对称轴为直线，D为对称轴上一动点．‎ （1） 求抛物线的解析式；‎ （2） 求当AD+CD最小时点的坐标；‎ （3） 以点为圆心，以为半径作⊙A．‎ ‎①证明：当AD+CD最小时，直线BD与⊙A相切．‎ ‎②写出直线BD与⊙A相切时，D点的另一个坐标：___________．‎ ‎18、（2009年内蒙古包头）已知二次函数（）的图象经过点，，，直线（）与轴交于点．‎ ‎（1）求二次函数的解析式；‎ ‎（2）在直线（）上有一点（点在第四象限），使得为顶点的三角形与以为顶点的三角形相似，求点坐标（用含的代数式表示）；‎ ‎（3）在（2）成立的条件下，抛物线上是否存在一点，使得四边形为平行四边形？若存在，请求出的值及四边形的面积；若不存在，请说明理由．‎ y x O ‎19、（2009山西省太原市）已知，二次函数的表达式为．写出这个函数图象的对称轴和顶点坐标，并求图象与轴的交点的坐标．‎ ‎20、（2009湖北省荆门市） 一开口向上的抛物线与x轴交于A（，0），B（m＋2，0）两点，记抛物线顶点为C，且AC⊥BC．‎ ‎（1）若m为常数，求抛物线的解析式；‎ ‎（2）若m为小于0的常数，那么（1）中的抛物线经过怎么样的平移可以使顶点在坐标原点？‎ ‎（3）设抛物线交y轴正半轴于D点，问是否存在实数m，使得△BCD为等腰三角形？若存在，求出m的值；若不存在，请说明理由．‎ O B A C D x y 第25题图 ‎20、（2009年淄博市）如图，在平面直角坐标系中，正方形OABC的边长是2．O为坐标原点，点A在x的正半轴上，点C在y的正半轴上．一条抛物线经过A点，顶点D是OC的中点．‎ ‎（1）求抛物线的表达式；‎ ‎（2）正方形OABC的对角线OB与抛物线交于E点，线段FG过点E与x轴垂直，分别交x轴和线段BC于F，G点，试比较线段OE与EG的长度；‎ O A B C D E y x F G H I J K ‎（第24题）‎ ‎（3）点H是抛物线上在正方形内部的任意一点，线段IJ过点H与x轴垂直，分别交x轴和线段BC于I、J点，点K在y轴的正半轴上，且OK=OH，请证明△OHI≌△JKC．‎ ‎21、（2009年贵州省黔东南州）凯里市某大型酒店有包房100间，在每天晚餐营业时间，每间包房收包房费100元时，包房便可全部租出；若每间包房收费提高20元，则减少10间包房租出，若每间包房收费再提高20元，则再减少10间包房租出，以每次提高20元的这种方法变化下去。‎ ‎（1）设每间包房收费提高x（元），则每间包房的收入为y1（元），但会减少y2间包房租出，请分别写出y1、y2与x之间的函数关系式。‎ ‎（2）为了投资少而利润大，每间包房提高x（元）后，设酒店老板每天晚餐包房总收入为y（元），请写出y与x之间的函数关系式，求出每间包房每天晚餐应提高多少元可获得最大包房费收入，并说明理由。‎ ‎22、（2009年贵州省黔东南州）已知二次函数。‎ ‎（1）求证：不论a为何实数，此函数图象与x轴总有两个交点。‎ ‎（2）设a<0，当此函数图象与x轴的两个交点的距离为时，求出此二次函数的解析式。‎ ‎（3）若此二次函数图象与x轴交于A、B两点，在函数图象上是否存在点P，使得△PAB的面积为，若存在求出P点坐标，若不存在请说明理由。‎ ‎23、（2009年江苏省）如图，已知二次函数的图象的顶点为．二次函数的图象与轴交于原点及另一点，它的顶点在函数的图象的对称轴上．‎ ‎（1）求点与点的坐标；‎ ‎（2）当四边形为菱形时，求函数的关系式．‎ ‎ ‎ ‎24、（2009年浙江省绍兴市）定义一种变换：平移抛物线得到抛物线，使经过的顶点．设的对称轴分别交于点，点是点关于直线的对称点．‎ ‎（1）如图1，若：，经过变换后，得到：，点的坐标为，则①的值等于______________；‎ ‎②四边形为（ ）‎ A．平行四边形 B．矩形 C．菱形 D．正方形 ‎（2）如图2，若：，经过变换后，点的坐标为，求的面积；‎ ‎（3）如图3，若：，经过变换后，，点是直线上的动点，求点到点的距离和到直线的距离之和的最小值．‎ ‎26、（2009年深圳市）已知：Rt△ABC的斜边长为5，斜边上的高为2，将这个直角三角形放置在平面直角坐标系中，使其斜边AB与x轴重合（其中OA0，n>0），连接DP交BC于点E。‎ 图11‎ ‎①当△BDE是等腰三角形时，直接写出此时点E的坐标。‎ ‎②又连接CD、CP，△CDP是否有最大面积？若有，求出△CDP的最大面的最大面积和此时点P的坐标；若没有，请说明理由。‎ ‎27、（2009年台州市）如图，已知直线交坐标轴于两点，以线段为边向上作正方形，过点的抛物线与直线另一个交点为．‎ ‎（1）请直接写出点的坐标； ‎ ‎（2）求抛物线的解析式；‎ ‎（3）若正方形以每秒个单位长度的速度沿射线下滑，直至顶点落在轴上时停止．设正方形落在轴下方部分的面积为，求关于滑行时间的函数关系式，并写出相应自变量的取值范围；‎ O A B C D E y x ‎（4）在（3）的条件下，抛物线与正方形一起平移，同时停止，求抛物线上两点间的抛物线弧所扫过的面积．‎ 备用图 ‎28、（2009年宁波市）如图，抛物线与轴相交于点A、B，且过点．‎ ‎（1）求的值和该抛物线顶点P的坐标；‎ A B P x y O ‎（第23题）‎ C（5,4）‎ ‎（2）请你设计一种平移的方法，使平移后抛物线的顶点落在第二象限，并写出平移后抛物线的解析式．‎ ‎29、(2009年义乌)如图，抛物线与轴的一个交点A在点（-2，0）和（-1，0）之间（包括这两点），顶点C是矩形DEFG上（包括边界和内部）的一个动点，则 ‎(填“”或“”)；‎ 的取值范围是 ‎ ‎ ‎30、（2009河池） ‎ O D B C A E 图12‎ 如图12，已知抛物线交轴于A、B两点，交轴于点C，抛物线的对称轴交轴于点E，点B的坐标为（，0）．‎ ‎（1）求抛物线的对称轴及点A的坐标；‎ ‎（2）在平面直角坐标系中是否存在点P，‎ 与A、B、C三点构成一个平行四边形？若存在，‎ 请写出点P的坐标；若不存在，请说明理由；‎ ‎（3）连结CA与抛物线的对称轴交于点D，在抛物线上是否存在 点M，使得直线CM把四边形DEOC分成面积相等的两部分？‎ 若存在，请求出直线CM的解析式；若不存在，请说明理由．‎ ‎31、（2009柳州）‎ O x y A B C D 图11‎ 如图11，已知抛物线（）与轴的一个交点为，与y轴的负半轴交于点C，顶点为D．‎ ‎（1）直接写出抛物线的对称轴，及抛物线与轴的另一个交点A的坐标；‎ ‎（2）以AD为直径的圆经过点C．‎ ‎①求抛物线的解析式；‎ ‎②点在抛物线的对称轴上，点在抛物线上，‎ 且以四点为顶点的四边形为平行四边形，求点的坐标． ‎ ‎32、(2009烟台市) 如图，抛物线与轴交于两点，与轴交于C点，且经过点，对称轴是直线，顶点是．‎ （1） 求抛物线对应的函数表达式；‎ （2） 经过两点作直线与轴交于点，在抛物线上是否存在这样的点，使以点为顶点的四边形为平行四边形？若存在，请求出点的坐标；若不存在，请说明理由；‎ （3） 设直线与y轴的交点是，在线段上任取一点（不与重合），经过三点的圆交直线于点，试判断的形状，并说明理由；‎ （4） 当是直线上任意一点时，（3）中的结论是否成立？（请直接写出结论）．‎ O B x y A M C ‎1‎ ‎33、（2009恩施市）如图，在中，的面积为25，点为边上的任意一点（不与、重合），过点作，交于点．设，以为折线将翻折（使落在四边形所在的平面内），所得的与梯形重叠部分的面积记为．‎ ‎（1）用表示的面积；‎ ‎（2）求出时与的函数关系式；‎ ‎（3）求出时与的函数关系式；‎ ‎34、．（2009年甘肃白银）［12分+附加4分］如图14（1），抛物线与x轴交于A、B两点，与y轴交于点C（0，）．［图14（2）、图14（3）为解答备用图］‎ ‎（1）　　　　　，点A的坐标为　　　　　　，点B的坐标为　　　　　；‎ ‎（2）设抛物线的顶点为M，求四边形ABMC的面积；‎ ‎（3）在x轴下方的抛物线上是否存在一点D，使四边形ABDC的面积最大？若存在，请求出点D的坐标；若不存在，请说明理由；‎ ‎（4）在抛物线上求点Q，使△BCQ是以BC为直角边的直角三角形．‎ 图14（1）　　　　　　图14（2）　　　　　　　　图14（3）‎ ‎35、（2009年甘肃庆阳）（10分）图19是二次函数的图象在x轴上方的一部分，若这段图象与x轴所围成的阴影部分面积为S，试求出S取值的一个范围．‎ 图19‎ ‎36（2009年甘肃庆阳）如图18，在平面直角坐标系中，将一块腰长为5的等腰直角三角板ABC放在第二象限，且斜靠在两坐标轴上，直角顶点C的坐标为（，0），点B在抛物线上．‎ ‎（1）点A的坐标为 ，点B的坐标为 ；‎ ‎（2）抛物线的关系式为 ；‎ ‎（3）设（2）中抛物线的顶点为D，求△DBC的面积；‎ ‎（4）将三角板ABC绕顶点A逆时针方向旋转90°，到达的位置．请判断点、是否在（2）中的抛物线上，并说明理由．‎ 图18‎ ‎37、（2009年广西南宁）如图14，要设计一个等腰梯形的花坛，花坛上底长米，下底长米，上下底相距米，在两腰中点连线（虚线）处有一条横向甬道，上下底之间有两条纵向甬道，各甬道的宽度相等．设甬道的宽为米．‎ ‎（1）用含的式子表示横向甬道的面积；‎ ‎（2）当三条甬道的面积是梯形面积的八分之一时，求甬道的宽；‎ ‎（3）根据设计的要求，甬道的宽不能超过6米.如果修建甬道的总费用（万元）与甬道的宽度成正比例关系，比例系数是5.7，花坛其余部分的绿化费用为每平方米0.02万元，那么当甬道的宽度为多少米时，所建花坛的总费用最少？最少费用是多少万元？‎ 图14‎ ‎38、(2009年鄂州)‎ ‎24、如图所示．某校计划将一块形状为锐角三角形ABC的空地进行生态环境改造．已知△ABC的边BC长‎120米，高AD长‎80米。学校计划将它分割成△AHG、△BHE、△GFC和矩形EFGH四部分(如图)。其中矩形EFGH的一边EF在边BC上．其余两个顶点H、G分别在边AB、AC上。现计划在△AHG上种草，每平方米投资6元；在△BHE、△FCG上都种花，每平方米投资10元；在矩形EFGH上兴建爱心鱼池，每平方米投资4元。‎ ‎(1)当FG长为多少米时，种草的面积与种花的面积相等？‎ ‎(2)当矩形EFGH的边FG为多少米时，△ABC空地改造总投资最小？最小值为多少？‎ ‎39、(2009年鄂州)如图所示，将矩形OABC沿AE折叠，使点O恰好落在BC上F处，以CF为边作正方形CFGH，延长BC至M，使CM＝｜CF—EO｜，再以CM、CO为边作矩形CMNO ‎(1)试比较EO、EC的大小，并说明理由 ‎(2)令，请问m是否为定值？若是，请求出m的值；若不是，请说明理由 ‎(3)在(2)的条件下，若CO＝1，CE＝，Q为AE上一点且QF＝，抛物线y＝mx2+bx+c经过C、Q两点，请求出此抛物线的解析式.‎ ‎ (4)在(3)的条件下，若抛物线y＝mx2+bx+c与线段AB交于点P，试问在直线BC上是否存在点K，使得以P、B、K为顶点的三角形与△AEF相似?若存在，请求直线KP与y轴的交点T的坐标?若不存在，请说明理由。‎ ‎40、（2009年河南）如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（4，0）、C（8，0）、D（8，8）.抛物线y=ax2+bx过A、C两点. ‎ ‎(1)直接写出点A的坐标，并求出抛物线的解析式；‎ ‎ (2)动点P从点A出发．沿线段AB向终点B运动，同时点Q从点C出发，沿线段CD 向终点D运动．速度均为每秒1个单位长度，运动时间为t秒.过点P作PE⊥AB交AC于点E ‎ ①过点E作EF⊥AD于点F，交抛物线于点G.当t为何值时，线段EG最长?‎ ‎②连接EQ．在点P、Q运动的过程中，判断有几个时刻使得△CEQ是等腰三角形?‎ 请直接写出相应的t值.‎ ‎ ‎ ‎41、如图，△OAB是边长为2的等边三角形，过点A的直线 （1） 求点E的坐标；‎ （2） 求过 A、O、E三点的抛物线解析式；‎ （3） 若点P是（2）中求出的抛物线AE段上一动点（不与A、E重合），设四边形OAPE的面积为S，求S的最大值。‎ ‎42、（2009江西）如图，抛物线与轴相交于、两点（点在点的左侧），与轴相交于点，顶点为.‎ ‎（1）直接写出、、三点的坐标和抛物线的对称轴； ‎ ‎（2）连接，与抛物线的对称轴交于点，点为线段上的一个动点，过点作交抛物线于点，设点的横坐标为；‎ ‎①用含的代数式表示线段的长，并求出当为何值时，四边形为平行四边形？‎ ‎②设的面积为，求与的函数关系式.‎ ‎43、（2009年烟台市） 某商场将进价为2000元的冰箱以2400元售出，平均每天能售出8台，为了配合国家“家电下乡”政策的实施，商场决定采取适当的降价措施.调查表明：这种冰箱的售价每降低50元，平均每天就能多售出4台．‎ ‎ （1）假设每台冰箱降价x元，商场每天销售这种冰箱的利润是y元，请写出y与x之间的函数表达式；（不要求写自变量的取值范围）‎ ‎ （2）商场要想在这种冰箱销售中每天盈利4800元，同时又要使百姓得到实惠，每台冰箱应降价多少元？‎ ‎ （3）每台冰箱降价多少元时，商场每天销售这种冰箱的利润最高？最高利润是多少？‎ ‎44、（2009年烟台市）如图，抛物线与轴交于两点，与轴交于C点，且经过点，对称轴是直线，顶点是．‎ （1） 求抛物线对应的函数表达式；‎ （2） 经过两点作直线与轴交于点，在抛物线上是否存在这样的点，使以点为顶点的四边形为平行四边形？若存在，请求出点的坐标；若不存在，请说明理由；‎ （3） 设直线与y轴的交点是，在线段上任取一点（不与重合），经过三点的圆交直线于点，试判断的形状，并说明理由；‎ （4） 当是直线上任意一点时，（3）中的结论是否成立？（请直接写出结论）．‎ O B x y A M C ‎1‎ ‎45、（2009年嘉兴市）如图，曲线C是函数在第一象限内的图象，抛物线是函数的图象．点（）在曲线C上，且都是整数．‎ ‎（1）求出所有的点；‎ ‎（2）在中任取两点作直线，求所有不同直线的条数；‎ ‎（3）从（2）的所有直线中任取一条直线，求所取直线与抛物线有公共点的概率．‎ ‎6‎ ‎4‎ ‎2‎ ‎2‎ ‎4‎ ‎6‎ y x O ‎46、(2009年牡丹江市)如图二次函数的图象经过和两点，且交轴于点．‎ ‎（1）试确定、的值；‎ ‎（2）过点作轴交抛物线于点点为此抛物线的顶点，试确定的形状．‎ ‎0‎ x y A B C ‎47、（2009南宁市）26．如图14，要设计一个等腰梯形的花坛，花坛上底长米，下底长米，上下底相距米，在两腰中点连线（虚线）处有一条横向甬道，上下底之间有两条纵向甬道，各甬道的宽度相等．设甬道的宽为米．‎ ‎（1）用含的式子表示横向甬道的面积；‎ ‎（2）当三条甬道的面积是梯形面积的八分之一时，求甬道的宽；‎ ‎（3）根据设计的要求，甬道的宽不能超过6米.如果修建甬道的总费用（万元）与甬道的宽度成正比例关系，比例系数是5.7，花坛其余部分的绿化费用为每平方米0.02万元，那么当甬道的宽度为多少米时，所建花坛的总费用最少？最少费用是多少万元？‎ ‎48、（2009年清远）已知二次函数中的满足下表：‎ ‎…‎ ‎0‎ ‎1‎ ‎2‎ ‎…‎ ‎…‎ ‎4‎ ‎0‎ ‎0‎ ‎…‎ 求这个二次函数关系式．‎ ‎49、（2009年清远）如图，已知一个三角形纸片，边的长为8，边上的高为，和都为锐角，为一动点（点与点不重合），过点作，交于点，在中，设的长为，上的高为．‎ ‎（1）请你用含的代数式表示．‎ ‎（2）将沿折叠，使落在四边形所在平面，设点落在平面的点为，与四边形重叠部分的面积为，当为何值时，最大，最大值为多少？‎ B C N M A ‎50、（2009年衢州）如图，已知点A(-4，8)和点B(2，n)在抛物线上．‎ ‎(1)　求a的值及点B关于x轴对称点P的坐标，并在x轴上找一点Q，使得AQ+QB最短，求出点Q的坐标；‎ ‎　(2)　平移抛物线，记平移后点A的对应点为A′，点B的对应点为B′，点C(-2，0)和点D(-4，0)是x轴上的两个定点．‎ ‎①　当抛物线向左平移到某个位置时，A′C+CB′ 最短，求此时抛物线的函数解析式；‎ ‎②　当抛物线向左或向右平移时，是否存在某个位置，使四边形A′B′CD的周长最短？若存在，求出此时抛物线的函数解析式；若不存在，请说明理由．‎ ‎4‎ x ‎2‎ ‎2‎ A ‎8‎ ‎-2‎ O ‎-2‎ ‎-4‎ y ‎6‎ B C D ‎-4‎ ‎4‎ ‎51、（2009年舟山）如图，已知点A(-4，8)和点B(2，n)在抛物线上．‎ ‎(1)　求a的值及点B关于x轴对称点P的坐标，并在x轴上找一点Q，使得AQ+QB最短，求出点Q的坐标；‎ ‎(2)　平移抛物线，记平移后点A的对应点为A′，点B的对应点为B′，点C(-2，0)和点D(-4，0)是x轴上的两个定点．‎ ‎①　当抛物线向左平移到某个位置时，A′C+CB′ 最短，求此时抛物线的函数解析式；‎ ‎②　当抛物线向左或向右平移时，是否存在某个位置，使四边形A′B′CD 的周长最短？若存在，求出此时抛物线的函数解析式；若不存在，请说明理由．‎ ‎4‎ x ‎2‎ ‎2‎ A ‎8‎ ‎-2‎ O ‎-2‎ ‎-4‎ y ‎6‎ B C D ‎-4‎ ‎4‎ ‎53、（2009年广州市）如图13，二次函数的图象与x轴交于A、B两点，与y轴交于点C（0，-1），ΔABC的面积为。‎ ‎（1）求该二次函数的关系式；‎ ‎（2）过y轴上的一点M（0，m）作y轴上午垂线，若该垂线与ΔABC的外接圆有公共点，求m的取值范围；‎ ‎（3）在该二次函数的图象上是否存在点D，使四边形ABCD为直角梯形？若存在，求出点D的坐标；若不存在，请说明理由。‎ ‎54、（2009年衡阳市）已知二次函数的图象过坐标原点，它的顶点坐标是（1，－2），求这个二次函数的关系式．‎ A2‎ ‎55、（2009年益阳市）阅读材料：‎ B C 铅垂高 水平宽 h ‎ a ‎ 图12-1‎ ‎ 如图12-1，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”(a)，中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法：，即三角形面积等于水平宽与铅垂高乘积的一半.‎ ‎ 解答下列问题：‎ ‎ 如图12-2，抛物线顶点坐标为点C(1,4),交x轴于点A(3,0)，交y轴于点B.‎ ‎(1)求抛物线和直线AB的解析式；‎ ‎(2)点P是抛物线(在第一象限内)上的一个动点，连结PA，PB，当P点运动到顶点C时，求△CAB的铅垂高CD及；‎ ‎ (3)是否存在一点P，使S△PAB=S△CAB，若存在，求出P点的坐标；若不存在，请说明理由.‎ 图12-2‎ x C O y A B D ‎1‎ ‎1‎ ‎ ‎ ‎56、（2009年济宁市）某体育用品商店购进一批滑板，每件进价为100元，售价为130元，每星期可卖出80件.商家决定降价促销，根据市场调查，每降价5元，每星期可多卖出20件.‎ ‎（1）求商家降价前每星期的销售利润为多少元？‎ ‎（2）降价后，商家要使每星期的销售利润最大，应将售价定为多少元？最大销售利润是多少？‎ ‎57、（2009年日照）某仓库为了保持库内的湿度和温度，四周墙上均装有如图所示的自动通风设施．该设施的下部ABCD是矩形，其中AB=‎2米，BC=‎1米；上部CDG是等边三角形，固定点E为AB的中点．△EMN是由电脑控制其形状变化的三角通风窗（阴影部分均不通风），MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆． ‎ ‎（1）当MN和AB之间的距离为‎0.5米时，求此时△EMN的面积； ‎ ‎（2）设MN与AB之间的距离为米，试将△EMN的面积S（平方米）表示成关于x的函数； ‎ ‎（3）请你探究△EMN的面积S（平方米）有无最大值，若有，请求出这个最大值；若没有，请说明理由． ‎ E A B G N D M C ‎（第23题图）‎ ‎58、（2009年福州）已知直线l：y=－x+m（m≠0）交x轴、y轴于A、B两点，点C、M分别在 线段OA、AB上，且OC=2CA，AM=2MB，连接MC，将△ACM绕点M旋转180°，得到△FEM，则点E在y轴上, 点F在直线l上;取线段EO中点N,将ACM沿MN所在直线翻折，得到△PMG，其中P与A为对称点.记：过点F的双曲线为，过点M且以B为顶点的抛物线为，过点P且以M图10‎ 为顶点的抛物线为.‎ ‎(1) 如图10，当m=6时，①直接写出点M、F的坐标，②求、的函数解析式；‎ ‎（2）当m发生变化时， ①在的每一支上，y随x的增大 如何变化？请说明理由。‎ ‎②若、中的y都随着x的增大而减小,写出x的取值范围。‎ ‎59、（2009年宜宾）如图，在平面直角坐标系O中，等腰梯形OABC的下底边OA在的正半轴上，BC∥OA，OC=AB，tan∠BAO=,点B的坐标为（7，4）。‎ ‎（1）求A、C的坐标；‎ ‎（2）求经过点O、B、C的抛物线的解析式；‎ ‎（3）在第一象限内（2）中的抛物线上是否存在一点P，使得经过点P且与等腰梯形一腰平行的直线将该梯形分成面积相等的两个部分？若存在，请求出点P的横坐标；若不存在，请说明理由．‎ H G ‎60、（2009年福州）如图9，等边边长为4，是边上动点，于H，过作∥，交线段于点，在线段上取点，使。设。‎ （1） 请直接写出图中与线段相等的两条线段（不再另外添加辅助线）；‎ （2） 是线段上的动点，当四边形EFPQ是平行四边形时,求□EFPQ的面积（用含的代数式表示）；‎ ‎（3） 当（2）中 的□EFPQ面积最大值时，以E为圆心，为半径作圆，根据⊙E与此时□EFPQ四条边交点的总个数，求相应的的取值范围。‎ ‎61、（2009年重庆）某电视机生产厂家去年销往农村的某品牌电视机每台的售价y（元）与月份x之间满足函数关系，去年的月销售量p（万台）与月份x之间成一次函数关系，其中两个月的销售情况如下表：‎ 月份 ‎1月 ‎5月 销售量 ‎3.9万台 ‎4.3万台 ‎（1）求该品牌电视机在去年哪个月销往农村的销售金额最大？最大是多少？‎ ‎（2）由于受国际金融危机的影响，今年1、2月份该品牌电视机销往农村的售价都比去年12月份下降了，且每月的销售量都比去年12月份下降了‎1.5m%．国家实施“家电下乡”‎ 政策，即对农村家庭购买新的家电产品，国家按该产品售价的13%给予财政补贴．受此政策的影响，今年3至5月份，该厂家销往农村的这种电视机在保持今年2月份的售价不变的情况下，平均每月的销售量比今年2月份增加了1.5万台．若今年3至5月份国家对这种电视机的销售共给予了财政补贴936万元，求的值（保留一位小数）．‎ ‎（参考数据：，，，）‎ ‎62、（2009年重庆）已知：如图，在平面直角坐标系中，矩形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA=2，OC=3．过原点O作∠AOC的平分线交AB于点D，连接DC，过点D作DE⊥DC，交OA于点E．‎ ‎（1）求过点E、D、C的抛物线的解析式；‎ ‎（2）将∠EDC绕点D按顺时针方向旋转后，角的一边与y轴的正半轴交于点F，另一边与线段OC交于点G．如果DF与（1）中的抛物线交于另一点M，点M的横坐标为，那么EF=2GO是否成立？若成立，请给予证明；若不成立，请说明理由；‎ ‎（3）对于（2）中的点G，在位于第一象限内的该抛物线上是否存在点Q，使得直线CQ与AB的交点P与点C、G构成的△PCG是等腰三角形？若存在，请求出点Q的坐标；若不存在，请说明理由．‎ ‎63、（2009年广西钦州）如图，已知抛物线y＝x2＋bx＋c与坐标轴交于A、B、C三点， A点的坐标为（－1，0），过点C的直线y＝x－3与x轴交于点Q，点P是线段BC上的一个动点，过P作PH⊥OB于点H．若PB＝5t，且0＜t＜1．‎ ‎（1）填空：点C的坐标是_▲_，b＝_▲_，c＝_▲_；‎ ‎（2）求线段QH的长（用含t的式子表示）；‎ ‎（3）依点P的变化，是否存在t的值，使以P、H、Q为顶点的三角形与△COQ相似？若存在，求出所有t的值；若不存在，说明理由．‎ ‎64、（2009年广西梧州）如图（9）-1，抛物线经过A（，0），C（3，）两点，与轴交于点D，与轴交于另一点B．‎ ‎（1）求此抛物线的解析式；‎ ‎（2）若直线将四边形ABCD面积二等分，求的值；‎ D O B A x y C y=kx+1‎ ‎（3）如图（9）-2，过点E（1，1）作EF⊥轴于点F，将△AEF绕平面内某点旋转180°得△MNQ（点M、N、Q分别与点A、E、F对应），使点M、N在抛物线上，作MG⊥轴于点G，若线段MG︰AG＝1︰2，求点M，N的坐标．‎ E F M N G O B A x y Q ‎65. (2009年甘肃定西)如图14（1），抛物线与x轴交于A、B两点，与y轴交于点C（0，）．［图14（2）、图14（3）为解答备用图］‎ ‎（1）　　　　　，点A的坐标为　　　　　　，点B的坐标为　　　　　；‎ ‎（2）设抛物线的顶点为M，求四边形ABMC的面积；‎ ‎（3）在x轴下方的抛物线上是否存在一点D，使四边形ABDC的面积最大？若存在，请求出点D的坐标；若不存在，请说明理由；‎ ‎（4）在抛物线上求点Q，使△BCQ是以BC为直角边的直角三角形．‎ ‎66、2009年包头）某商场试销一种成本为每件60元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于45%，经试销发现，销售量（件）与销售单价（元）符合一次函数，且时，；时，．‎ ‎（1）求一次函数的表达式；‎ ‎（2）若该商场获得利润为元，试写出利润与销售单价之间的关系式；销售单价定为多少元时，商场可获得最大利润，最大利润是多少元？‎ ‎（3）若该商场获得利润不低于500元，试确定销售单价的范围．‎ ‎67、（2009年包头）已知二次函数（）的图象经过点，，，直线（）与轴交于点．‎ ‎（1）求二次函数的解析式；‎ ‎（2）在直线（）上有一点（点在第四象限），使得为顶点的三角形与以 为顶点的三角形相似，求点坐标（用含的代数式表示）；‎ ‎（3）在（2）成立的条件下，抛物线上是否存在一点，使得四边形为平行四边形？若存在，请求出的值及四边形的面积；若不存在，请说明理由．‎ y x O ‎68、（2009年长沙）如图，二次函数（）的图象与轴交于两点，与轴相交于点．连结两点的坐标分别为、，且当和时二次函数的函数值相等．‎ ‎（1）求实数的值；‎ ‎（2）若点同时从点出发，均以每秒1个单位长度的速度分别沿边运动，其中一个点到达终点时，另一点也随之停止运动．当运动时间为秒时，连结，将沿翻折，点恰好落在边上的处，求的值及点的坐标；‎ ‎（3）在（2）的条件下，二次函数图象的对称轴上是否存在点，使得以为项点的三角形与相似？如果存在，请求出点的坐标；如果不存在，请说明理由．‎ y O x C N B P M A ‎（3）点是抛物线对称轴右侧图象上的一动点，过点作交轴于点，是否存在点使得与相似？若存在，请求出所有符合条件的点的坐标；若不存在，请说明理由．‎ ‎70、(2009宁夏)如图，抛物线与轴交于两点，与轴交于点．‎ ‎（1）求三点的坐标；‎ ‎（2）证明为直角三角形；‎ y x B O A C ‎（3）在抛物线上除点外，是否还存在另外一个点，使是直角三角形，若存在，请求出点的坐标，若不存在，请说明理由．‎ ‎71、（2009肇庆）已知一元二次方程的一根为 2． ‎ ‎（1）求关于的关系式； ‎ ‎（2）求证：抛物线与轴有两个交点； ‎ ‎（3）设抛物线的顶点为 M，且与 x 轴相交于A（，0）、B（，0）两点，求使△AMB 面积最小时的抛物线的解析式． ‎ ‎72、1．（2009年中山）正方形边长为4，、分别是、上的两个动点，当点在上运动时，保持和垂直，‎ ‎（1）证明：；‎ ‎（2）设，梯形的面积为，求与之间的函数关系式；当点运动到什么位置时，四边形面积最大，并求出最大面积；‎ ‎（3）当点运动到什么位置时，求的值．‎ ‎2．（2009年漳州）阅读材料，解答问题．‎ 例：用图象法解一元二次不等式：．‎ 解：设，则是的二次函数．‎ ‎∴抛物线开口向上．‎ 又当时，，‎ 解得．‎ 由此得抛物线的大致图象如图所示．‎ 观察函数图象可知：当或时，．‎ 的解集是：或．‎ ‎（1）观察图象，直接写出一元二次不等式：的解集是____________；‎ ‎（2）仿照上例，用图象法解一元二次不等式：．（大致图象画在答题卡上）‎ ‎75、（2009年漳州）如图1，已知：抛物线与轴交于两点，与轴交于点，经过两点的直线是，连结．‎ ‎（1）两点坐标分别为（_____，_____）、（_____，_____），抛物线的函数关系式为______________；‎ ‎（2）判断的形状，并说明理由；‎ ‎（3）若内部能否截出面积最大的矩形（顶点在各边上）？若能，求出在边上的矩形顶点的坐标；若不能，请说明理由．‎ ‎ [抛物线的顶点坐标是]‎ C A O B x y C A O B x y 图1‎ 图2(备用)‎ ‎76、（2009年哈尔滨）张大爷要围成一个矩形花圃．花圃的一边利用足够长的墙另三边用总长为32米的篱笆恰好围成．围成的花圃是如图所示的矩形ABCD．设AB边的长为x米．矩形ABCD的面积为S平方米．‎ ‎ （1）求S与x之间的函数关系式（不要求写出自变量x的取值范围）．‎ ‎ （2）当x为何值时，S有最大值？并求出最大值．‎ ‎（参考公式：二次函数（），当时，)‎ ‎77、（2009年牡丹江）如图二次函数的图象经过和两点，且交轴于点．‎ ‎（1）试确定、的值；‎ ‎（2）过点作轴交抛物线于点点为此抛物线的顶点，试确定的形状．‎ 参考公式：顶点坐标 ‎ ‎78、（2009年兰州）如图17，某公路隧道横截面为抛物线，其最大高度为‎6米，底部宽度OM为‎12米. 现以O点为原点，OM所在直线为x轴建立直角坐标系.‎ ‎(1)直接写出点M及抛物线顶点P的坐标；‎ ‎(2)求这条抛物线的解析式；‎ ‎(3)若要搭建一个矩形“支撑架”AD- DC- CB，‎ 使C、D点在抛物线上，A、B点在地面OM上，‎ 则这个“支撑架”总长的最大值是多少？‎ ‎77、（2009年遂宁）25.如图，二次函数的图象经过点D(0，)，且顶点C的横坐标为4，该图象在x 轴上截得的线段AB的长为6.‎ ‎⑴求二次函数的解析式；‎ ‎⑵在该抛物线的对称轴上找一点P，使PA+PD最小，求出点P的坐标；‎ ‎⑶在抛物线上是否存在点Q，使△QAB与△ABC相似？如果存在，求出点Q的坐标；如果不存在，请说明理由．‎ ‎8、（2009年济南）已知：抛物线的对称轴为与轴交于两点，与轴交于点其中、‎ ‎（1）求这条抛物线的函数表达式．‎ ‎（2）已知在对称轴上存在一点P，使得的周长最小．请求出点P的坐标．‎ ‎（3）若点是线段上的一个动点（不与点O、点C重合）．过点D作交轴于点连接、．设的长为，的面积为．求与之间的函数关系式．试说明是否存在最大值，若存在，请求出最大值；若不存在，请说明理由．‎ A C x y B O ‎9、（2009年凉山州）如图，已知抛物线经过，两点，顶点为．‎ ‎（1）求抛物线的解析式；‎ ‎（2）将绕点顺时针旋转90°后，点落到点的位置，将抛物线沿轴平移后经过点，求平移后所得图象的函数关系式；‎ y x B A O D ‎（第26题）‎ ‎（3）设（2）中平移后，所得抛物线与轴的交点为，顶点为，若点在平移后的抛物线上，且满足的面积是面积的2倍，求点的坐标．‎ ‎83、（2009年广州市）如图13，二次函数 的图象与x轴交于A、B两点，与y轴交于点C（0，-1），ΔABC的面积为。‎ ‎（1）求该二次函数的关系式；‎ ‎（2）过y轴上的一点M（0，m）作y轴上午垂线，若该垂线与ΔABC的外接圆有公共点，求m的取值范围；‎ ‎（3）在该二次函数的图象上是否存在点D，使四边形ABCD为直角梯形？若存在，求出点D的坐标；若不存在，请说明理由。‎ ‎4.（2009年衡阳市）已知二次函数的图象过坐标原点，它的顶点坐标是（1，－2），求这个二次函数的关系式．‎ A2‎ ‎5.（2009年益阳市）阅读材料：‎ B C 铅垂高 水平宽 h ‎ a ‎ 图12-1‎ ‎ 如图12-1，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”(a)，中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法：，即三角形面积等于水平宽与铅垂高乘积的一半.‎ ‎ 解答下列问题：‎ ‎ 如图12-2，抛物线顶点坐标为点C(1,4),交x轴于点A(3,0)，交y轴于点B.‎ ‎(1)求抛物线和直线AB的解析式；‎ ‎(2)点P是抛物线(在第一象限内)上的一个动点，连结PA，PB，当P点运动到顶点C时，求△CAB的铅垂高CD及；‎ ‎ (3)是否存在一点P，使S△PAB=S△CAB，若存在，求出P点的坐标；若不存在，请说明理由.‎ 图12-2‎ x C O y A B D ‎1‎ ‎1‎ ‎ ‎ ‎89、（2009年济宁市）某体育用品商店购进一批滑板，每件进价为100元，售价为130元，每星期可卖出80件.商家决定降价促销，根据市场调查，每降价5元，每星期可多卖出20件.‎ ‎（1）求商家降价前每星期的销售利润为多少元？‎ ‎（2）降价后，商家要使每星期的销售利润最大，应将售价定为多少元？最大销售利润是多少？‎ ‎90、（2009年株洲市）如图1，中，，，点在线段上运动，点、分别在线段、上，且使得四边形是矩形．设的长为，矩形的面积为 ‎，已知是的函数，其图象是过点（12，36）的抛物线的一部分（如图2所示）．‎ ‎（1）求的长；‎ ‎（2）当为何值时，矩形的面积最大，并求出最大值．‎ 为了解决这个问题，孔明和研究性学习小组的同学作了如下讨论： ‎ 张明：图2中的抛物线过点（12，36）在图1中表示什么呢？‎ 李明：因为抛物线上的点是表示图1中的长与矩形面积的对应关系，那么，（12，36）表示当时，的长与矩形面积的对应关系.‎ 赵明：对，我知道纵坐标36是什么意思了！‎ 孔明：哦，这样就可以算出，这个问题就可以解决了.‎ ‎ 请根据上述对话，帮他们解答这个问题.‎ O ‎ ‎ 图1 图2‎ ‎3.（2009年株洲市）已知为直角三角形，，,点、在轴上，点坐标为（，）（），线段与轴相交于点，以（1，0）为顶点的抛物线过点、．‎ ‎（1）求点的坐标（用表示）；‎ ‎（2）求抛物线的解析式；‎ ‎ ‎ ‎ ‎ ‎（3）设点为抛物线上点至点之间的一动点，连结并延长交于点，连结 并延长交于点，试证明：为定值．‎ ‎93. （2009年重庆市江津区）某商场在销售旺季临近时 ，某品牌的童装销售 价格呈上升趋势，假如这种童装开始时的售价为每件20元，并且每周（7天）涨价2元，从第6周开始，保持每件30元的稳定价格销售，直到11周结束，该童装不再销售。‎ ‎ （1）请建立销售价格y（元）与周次x之间的函数关系；‎ ‎ （2）若该品牌童装于进货当周售完，且这种童装每件进价z（元）与周次x之间的关系为， 1≤ x ≤11，且x为整数，那么该品牌童装在第几周售出后，每件获得利润最大？并求最大利润为多少？‎ ‎94、 （2009年重庆市江津区）如图，抛物线与x轴交与A(1,0),B(- 3，0)两点，‎ ‎ （1）求该抛物线的解析式；‎ ‎（2）设（1）中的抛物线交y轴与C点，在该抛物线的对称轴上是否存在点Q，使得△QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由.‎ ‎（3）在（1）中的抛物线上的第二象限上是否存在一点P，使△PBC的面积最大？，若存在，求出点P的坐标及△PBC的面积最大值.若没有，请说明理由.‎ ‎ ‎ ‎【关键词】与二次函数有关的面积问题 第26题图 ‎95、(2009年宁德市)如图，已知抛物线C1：的顶点为P，与x轴相交于A、B两点（点A在点B的左边），点B的横坐标是1．‎ ‎（1）求P点坐标及a的值；（4分）‎ ‎（2）如图（1），抛物线C2与抛物线C1关于x轴对称，将抛物线C2向右平移，平移后的抛物线记为C3，C3的顶点为M，当点P、M关于点B成中心对称时，求C3的解析式；（4分）‎ ‎（3）如图（2），点Q是x轴正半轴上一点，将抛物线C1绕点Q旋转180°后得到抛物线C4．抛物线C4的顶点为N，与x轴相交于E、F两点（点E在点F的左边），当以点P、N、F为顶点的三角形是直角三角形时，求点Q的坐标．（5分）‎ ‎【关键词】y x A O B P N 图2‎ C1‎ C4‎ Q E F 图（2）‎ y x A O B P M 图1‎ C1‎ C2‎ C3‎ 图（1）‎ 二次函数,勾股定理的运用 y x A O B P M 图(1)‎ C1‎ C2‎ C3‎ H G 解：（1）由抛物线C1：得 顶点P的为（-2，-5） ‎ ‎∵点B（1，0）在抛物线C1上 ‎∴‎ ‎ 解得，a＝ ‎ ‎（2）连接PM，作PH⊥x轴于H，作MG⊥x轴于G ‎∵点P、M关于点B成中心对称 ‎∴PM过点B，且PB＝MB ‎∴△PBH≌△MBG y x A O B P N 图(2)‎ C1‎ C4‎ Q E F H G K ‎∴MG＝PH＝5，BG＝BH＝3‎ ‎∴顶点M的坐标为（4，5） ‎ ‎ 抛物线C2由C1关于x轴对称得到，抛物线C3由C2平移得到 ‎∴抛物线C3的表达式为 ‎ ‎（3）∵抛物线C4由C1绕点x轴上的点Q旋转180°得到 ‎∴顶点N、P关于点Q成中心对称 ‎ 由（2）得点N的纵坐标为5‎ 设点N坐标为（m，5） ‎ ‎ 作PH⊥x轴于H，作NG⊥x轴于G ‎ 作PK⊥NG于K ‎ ∵旋转中心Q在x轴上 ‎∴EF＝AB＝2BH＝6‎ ‎ ∴FG＝3，点F坐标为（m+3，0）‎ ‎ H坐标为（2，0），K坐标为（m，-5），‎ 根据勾股定理得 ‎ PN2＝NK2+PK2＝m2+‎4m+104‎ ‎ PF2＝PH2+HF2＝m2+‎10m+50‎ ‎ NF2＝52+32＝34 ‎ ‎ ①当∠PNF＝90º时，PN2+ NF2＝PF2，解得m＝，∴Q点坐标为（，0） ‎ ‎②当∠PFN＝90º时，PF2+ NF2＝PN2，解得m＝，∴Q点坐标为（，0）‎ ‎③∵PN＞NK＝10＞NF，∴∠NPF≠90º 综上所得，当Q点坐标为（，0）或（，0）时，以点P、N、F为顶点 的三角形是直角三角形． ‎ ‎4.(2009年河北)已知抛物线经过点和点P （t，0），且t ≠ 0．‎ A O P x y 图12‎ ‎- 3‎ ‎- 3‎ ‎（1）若该抛物线的对称轴经过点A，如图12，‎ 请通过观察图象，指出此时y的最小值，‎ 并写出t的值； ‎ ‎（2）若，求a、b的值，并指出此时抛 物线的开口方向；‎ ‎（3）直接写出使该抛物线开口向下的t的一个值．‎ ‎98、(2009年潍坊)如图，在平面直角坐标系中，半径为1的圆的圆心在坐标原点，且与两坐标轴分别交于四点．抛物线与轴交于点，与直线交于点，且分别与圆相切于点和点．‎ ‎（1）求抛物线的解析式；‎ ‎（2）抛物线的对称轴交轴于点，连结，并延长交圆于，求的长．‎ ‎（3）过点作圆的切线交的延长线于点，判断点是否在抛物线上，说明理由．‎ O x y N C D E F B M A ‎99、（09湖北宜昌）已知：直角梯形OABC的四个顶点是O(0，0)，A(，1)， B(s，t)，C(，0)，抛物线y=x2＋mx－m的顶点P是直角梯形OABC内部或边上的一个动点，m为常数．‎ ‎(1)求s与t的值，并在直角坐标系中画出直角梯形OABC；‎ ‎(2)当抛物线y=x2＋mx－m与直角梯形OABC的边AB相交时，求m的取值范围．‎ ‎ ‎ ‎（第24题）‎ ‎100、（09湖南怀化）如图11，已知二次函数的图象与轴相交于两个不同的点、，与轴的交点为．设的外接圆的圆心为点．‎ ‎（1）求与轴的另一个交点D的坐标；‎ ‎（2）如果恰好为的直径，且的面积等于，求和的值． ‎ 解得 ‎101、（09湖南邵阳）如图（十二），直线的解析式为，它与轴、轴分别相交于两点．平行于直线的直线从原点出发，沿轴的正方形以每秒1个单位长度的速度运动，它与轴、轴分别相交于两点，设运动时间为秒（）．‎ ‎（1）求两点的坐标；‎ O M A P N y l m x B O M A P N y l m x B E P F 图十二 ‎（2）用含的代数式表示的面积；‎ ‎（3）以为对角线作矩形，记和重合部分的面积为，‎ ‎①当时，试探究与之间的函数关系式；‎ ‎②在直线的运动过程中，当为何值时，‎ 为面积的？‎ ‎102、（2009安徽年）23．已知某种水果的批发单价与批发量的函数关系如图（1）所示．‎ ‎（1）请说明图中①、②两段函数图象的实际意义．‎ ‎【解】‎ ‎（2）写出批发该种水果的资金金额w（元）与批发量m（kg）之间的 函数关系式；在下图的坐标系中画出该函数图象；指出金额在什 么范围内，以同样的资金可以批发到较多数量的该种水果．‎ ‎【解】‎ ‎（3）经调查，某经销商销售该种水果的日最高销量与零售价之间的函 数关系如图（2）所示，该经销商拟每日售出60kg以上该种水果，‎ 且当日零售价不变，请你帮助该经销商设计进货和销售的方案，‎ 使得当日获得的利润最大．‎ ‎【解】‎ ‎（2009年湖北荆州）已知：点P（，）关于轴的对称点在反比例函数的图像上，‎ 关于的函数的图像与坐标轴只有两个不同的交点A﹑B，求P点坐标和△PAB的面积.‎ ‎（2009年湖北荆州）由于国家重点扶持节能环保产业，某种节能产品的销售市场逐渐回暖．某经销商销售这种产品，年初与生产厂家签订了一份进货合同，约定一年内进价为0.1万元／台，并预付了5万元押金。他计划一年内要达到一定的销售量，且完成此销售量所用的进货总金额加上押金控制在不低于34万元，但不高于40万元．若一年内该产品的售价（万元／台）与月次（且为整数）满足关系是式：‎ ‎，一年后发现实际每月的销售量（台）与月次之间存在如图所示的变化趋势．‎ ‎⑴ 直接写出实际每月的销售量（台）与月次之间 的函数关系式；‎ ‎⑵ 求前三个月中每月的实际销售利润（万元）与月 次之间的函数关系式；‎ ‎⑶ 试判断全年哪一个月的的售价最高，并指出最高售价；‎ ‎⑷ 请通过计算说明他这一年是否完成了年初计划的销售量．‎ ‎36‎ ‎4月 ‎20‎ ‎40‎ Ｏ ‎（台）‎ ‎12月 ‎（2009年茂名市）如图，把抛物线与直线围成的图形绕原点顺时针旋转后，再沿轴向右平移1个单位得到图形则下列结论错误的是（ ）‎ A．点的坐标是 　 　B．点的坐标是 C．四边形是矩形 D．若连接则梯形的面积是3‎ O y x B ‎103、（2009年茂名市）茂名石化乙烯厂某车间生产甲、乙两种塑料的相关信息如下表，请你解答下列问题：‎ 价 目 品 种 出厂价 成本价 排污处理费 甲种塑料 ‎2100（元/吨）‎ ‎800（元/吨）‎ ‎200（元/吨）‎ 乙种塑料 ‎2400（元/吨）‎ ‎1100（元/吨）‎ ‎100（元/吨）‎ 每月还需支付设备管理、‎ 维护费20000元 ‎ （1）设该车间每月生产甲、乙两种塑料各吨，利润分别为元和元，分别求和 与的函数关系式（注：利润=总收入-总支出）；（6分）‎ ‎ （2）已知该车间每月生产甲、乙两种塑料均不超过400吨，若某月要生产甲、乙两种塑料共700吨，求该月生产甲、乙塑料各多少吨，获得的总利润最大？最大利润是多少？（4分）‎ ‎104、（2009年茂名市）如图，在中，点是边上的动点（点与点不重合），过动点作交于点 ‎ （1）若与相似，则是多少度？ （2分）‎ ‎ （2）试问：当等于多少时，的面积最大？最大面积是多少？ （4分）‎ ‎ （3）若以线段为直径的圆和以线段为直径的圆相外切，求线段的长．（4分）‎ ‎60°‎ A D C B P ‎105、1．（2009年湖北十堰市）如图①， 已知抛物线（a≠0）与轴交于点A(1，0)和点B (－3，0)，与y轴交于点C．‎ ‎(1) 求抛物线的解析式；‎ ‎(2) 设抛物线的对称轴与轴交于点M ，问在对称轴上是否存在点P，使△CMP为等腰三角形？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．‎ ‎ (3) 如图②，若点E为第二象限抛物线上一动点，连接BE、CE，求四边形BOCE面积的最大值，并求此时E点的坐标．‎ ‎25‎ ‎24‎ y2（元）‎ x（月）‎ ‎1 2 3 4 5 6 7 8 9 10 11 12 ‎ 第2题图 O ‎107、（2009年山东青岛市）某水产品养殖企业为指导该企业某种水产品的养殖和销售，对历年市场行情和水产品养殖情况进行了调查．调查发现这种水产品的每千克售价（元）与销售月份（月）满足关系式，而其每千克成本（元）与销售月份（月）满足的函数关系如图所示．‎ ‎（1）试确定的值；‎ ‎（2）求出这种水产品每千克的利润（元）与销售月份（月）之间的函数关系式；‎ ‎（3）“五·一”之前，几月份出售这种水产品每千克的利润最大？最大利润是多少？‎ ‎108、（2009年新疆乌鲁木齐市）如图9，在矩形中，已知、两点的坐标分别为，为的中点．设点是平分线上的一个动点（不与点重合）．‎ y O x P D B 图9‎ ‎（1）试证明：无论点运动到何处，总与相等；‎ ‎（2）当点运动到与点的距离最小时，试确定过三点的抛物线的解析式；‎ ‎（3）设点是（2）中所确定抛物线的顶点，当点运动到何处时，‎ 的周长最小？求出此时点的坐标和的周长；‎ ‎（4）设点是矩形的对称中心，是否存在点，使？若存在，请直接写出点的坐标．‎ ‎109、19．（2009 年佛山市）（1）请在坐标系中画出二次函数的大致图象；‎ ‎（2）在同一个坐标系中画出的图象向上平移两个单位后的图象；‎ ‎（3）直接写出平移后的图象的解析式.‎ x y O 第19题图 注：图中小正方形网格的边长为1.‎ ‎110、（2009年广东省）正方形边长为4，、分别是、上的两个动点， 当点在上运动时，保持和垂直，‎ ‎（1）证明：；‎ ‎（2）设，梯形的面积为，求与之间的函数关系式；当点运动到什么位置时，四边形面积最大，并求出最大面积；‎ ‎（3）当点运动到什么位置时，求此时的值．‎ D M A B C N ‎111、（2009年山西省）某批发市场批发甲、乙两种水果，根据以往经验和市场行情，预计夏季某一段时间内，甲种水果的销售利润（万元）与进货量（吨）近似满足函数关系；乙种水果的销售利润（万元）与进货量（吨）近似满足函数关系（其中为常数），且进货量为1吨时，销售利润为1.4万元；进货量为2吨时，销售利润为2.6万元．‎ ‎（1）求（万元）与（吨）之间的函数关系式．‎ ‎（2）如果市场准备进甲、乙两种水果共10吨，设乙种水果的进货量为吨，请你写出这两种水果所获得的销售利润之和（万元）与（吨）之间的函数关系式．并求出这两种水果各进多少吨时获得的销售利润之和最大，最大利润是多少？‎ ‎112、（2009年黄石市）已知关于的函数（为常数）‎ ‎（1）若函数的图象与轴恰有一个交点，求的值；‎ ‎（2）若函数的图象是抛物线，且顶点始终在轴上方，求的取值范围．‎ ‎113．（2009年黄石市）为了扩大内需，让惠于农民，丰富农民的业余生活，鼓励送彩电下乡，国家决定对购买彩电的农户实行政府补贴．规定每购买一台彩电，政府补贴若干元，经调查某商场销售彩电台数（台）与补贴款额（元）之间大致满足如图①所示的一次函数关系．随着补贴款额的不断增大，销售量也不断增加，但每台彩电的收益（元）会相应降低且与之间也大致满足如图②所示的一次函数关系．‎ ‎1200‎ ‎800‎ ‎0‎ ‎400‎ y(台)‎ x(元)‎ z(元)‎ x(元)‎ ‎200‎ ‎160‎ ‎200‎ ‎0‎ 图①‎ 图②‎ ‎（1）在政府未出台补贴措施前，该商场销售彩电的总收益额为多少元？‎ ‎（2）在政府补贴政策实施后，分别求出该商场销售彩电台数和每台家电的收益与政府补贴款额之间的函数关系式；‎ ‎（3）要使该商场销售彩电的总收益（元）最大，政府应将每台补贴款额定为多少？并求出总收益的最大值．‎ ‎113、（2009年黄石市）正方形在如图所示的平面直角坐标系中，在轴正半轴上，在轴的负半轴上，交轴正半轴于交轴负半轴于，，抛物线过三点．‎ ‎（1）求抛物线的解析式；（3分）‎ ‎（2）是抛物线上间的一点，过点作平行于轴的直线交边于，交所在直线于，若，则判断四边形的形状；（3分）‎ ‎（3）在射线上是否存在动点，在射线上是否存在动点，使得且，若存在，请给予严格证明，若不存在，请说明理由．（4分）‎ O y x B E A D C F ‎114、(2009年云南省)如图，在平面直角坐标系中，是坐标原点，点A、B的坐标分别为和，连结．‎ ‎（1）现将绕点A按逆时针方向旋转90°得到，请画出，并直接写出点、的坐标（注：不要求证明）；‎ ‎（2）求经过、、三点的抛物线对应的函数关系式，并画出抛物线的略图．‎ ‎115、（2009年枣庄市）如图，抛物线的顶点为A（2，1），且经过原点O，与x轴的另一个交点为B．‎ ‎（1）求抛物线的解析式；‎ ‎（2）在抛物线上求点M，使△MOB的面积是△AOB面积的3倍；‎ ‎（3）连结OA，AB，在x轴下方的抛物线上是否存在点N，使△OBN与△OAB相似？若存在，求出N点的坐标；若不存在，说明理由．‎ y x O A B 第24题图