2012年江苏省盐城市中考数学试题（含答案） 11页

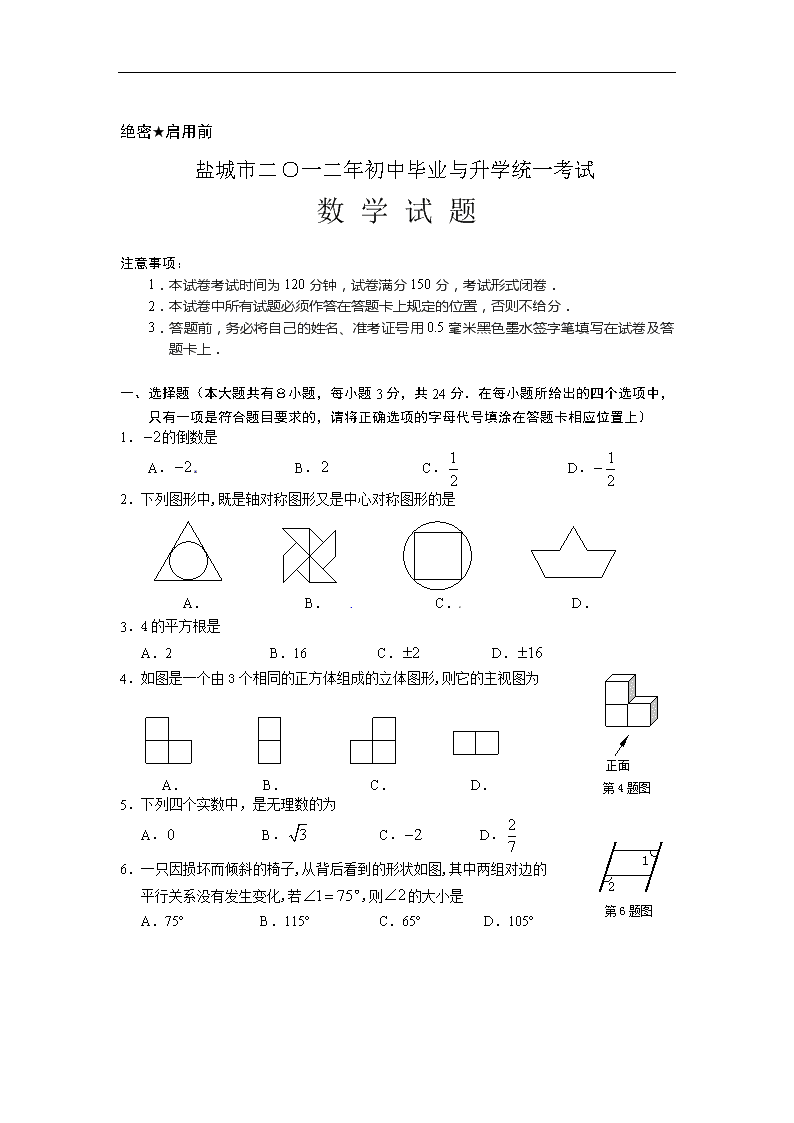
绝密★启用前 盐城市二○一二年初中毕业与升学统一考试 数 学 试 题 注意事项： 　　1．本试卷考试时间为 120 分钟，试卷满分 150 分，考试形式闭卷． 　　2．本试卷中所有试题必须作答在答题卡上规定的位置，否则不给分． 　　3．答题前，务必将自己的姓名、准考证号用 0.5 毫米黑色墨水签字笔填写在试卷及答 题卡上． 一、选择题（本大题共有８小题，每小题 3 分，共 24 分．在每小题所给出的四个选项中， 只有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上） 1． 的倒数是 A． B． C． D． 2．下列图形中,既是轴对称图形又是中心对称图形的是 A． B． C． D． 3．4 的平方根是 A．2 B．16 C． D． 4．如图是一个由 3 个相同的正方体组成的立体图形,则它的主视图为 A． B． C． D． 5．下列四个实数中，是无理数的为 A． B． C． D． 6．一只因损坏而倾斜的椅子,从背后看到的形状如图,其中两组对边的 平行关系没有发生变化,若 º,则 的大小是 A．75º B．115º C．65º D．105º 2− 2− 2 1 2 1 2 − 2± 16± 0 3 2− 2 7 1 75∠ = 2∠ 第 6 题图 1 2 第 4 题图 正面 7．甲、乙、丙、丁四人进行射击测试,每人 10 次射击的平均成绩恰好都是 9.4 环,方差分别 是 , , , .在本次射击测试中,成绩最稳定的 是 A．甲 B．乙 C．丙 D．丁 8 ． 已 知 整 数 满 足 下 列 条 件 ： , , , ,…,依次类推,则 的值为 A． B． C． D． 二、填空题（本大题共有 10 小题，每小题 3 分，共 30 分．不需写出解答过程，请将答案直 接写在答题卡相应位置上） 9．若二次根式 有意义,则 的取值范围是 ▲ . 10．分解因式: ＝ ▲ . 11． 中 国共产党第十八次全国代表大会将于 2012 年 10 月 15 日至 18 日在北京召开.据统 计,截至 2011 年底,全国的共产党员人数已超过 80 300 000,这个数据用科学计数法可表 示 为 ▲ . 12．若 ,则代数式 的值为 ▲ . 13．小勇第一次抛一枚质地均匀的硬币时正面向上,他第二次再抛这枚硬币时,正面向上的概 率是 ▲ . 14．若反比例函数的图象经过点 ,则它的函数关系式是 ▲ . 15．如图,在四边形 中,已知 ∥ , .在不添加任何辅助线的前提下, 要想该四边形成为矩形,只需再加上的一个条件是 ▲ .(填上你认为正确的一个 答案即可) 16．如图,在 中, 、 分别是边 、 的中点, º.现将 沿 折叠,点 落在三角形所在平面内的点为 ,则 的度数为 ▲ °. 17．已知 与 的半径分别是方程 的两根,且 ,若这两个 圆相切,则 ＝ ▲ . 18．一批志愿者组成了一个“爱心团队”,专门到全国各地巡回演出,以募集爱心基金.第一 个月他们就募集到资金 1 万元,随着影响的扩大,第 ( ≥2)个月他们募集到的资金都 将会比上个月增加 20%,则当该月所募集到的资金首次突破 10 万元时,相应的 的值 为 ▲ .(参考数据: , , ) 2 0.90S =甲 2 1.22S =乙 2 0.43S =丙 2 1.68S =丁 1 2 3 4, , , ,a a a a ⋅⋅⋅ 1 0a = 2 1| 1|a a= − + 3 2| 2 |a a= − + 4 3| 3|a a= − + 2012a 1005− 1006− 1007− 2012− 1x + x 2 24a b− 1x = − 3 2 4x x− + ( 1,4)P − ABCD AB DC AB DC= ABC∆ D E AB AC 50B∠ = ADE∆ DE A 1A 1BDA∠ 1O 2O 2 4 3 0x x− + = 1 2 2O O t= + t n n n 51.2 2.5≈ 61.2 3.0≈ 71.2 3.6≈ 第 15 题图 A B CD 第 16 题图 B A C D E A1 三、解答题（本大题共有 10 小题，共 96 分．请在答题卡指定区域内作答，解答时应写出文 字说明、推理过程或演算步骤） 19．（本题满分 8 分） （1）计算: （2）化简: 20．（本题满分 8 分） 解方程: 21．（本题满分 8 分） 现有形状、大小和颜色完全一样的三张卡片,上面分别标有数字“1”、“2”、“3”.第一次 从这三张卡片中随机抽取一张,记下数字后放回；第二次再从这三张卡片中随机抽取一张 并记下数字.请用列表或画树状图的方法表示出上述试验所有可能的结果,并求第二次抽 取的数字大于第一次抽取的数字的概率. 22．（本题满分 8 分） 第三十届夏季奥林匹克运动会将于 2012 年 7 月 27 日至 8 月 12 日在英国伦敦举行,目前 正在进行火炬传递活动.某校学生会为了确定近期宣传专刊的主题,想知道学生对伦敦奥 运火炬传递路线的了解程度,决定随机抽取部分学生进行一次问卷调查,并根据收集到的 信息进行了统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解 答下列问题: (1) 接受问卷调查的学生共有___________名； (2) 请补全折线统计图,并求出扇形统计图中“基本了解”部分所对应扇形的圆心角的大 小； (3) 若该校共有 1200 名学生,请根据上述调查结果估计该校学生中对伦敦奥运火炬传递 路线达到“了解”和“基本了解”程度的总人数. [来源:学§科§网] 01| | 2012 sin302 − − − ° 2( ) (2 )a b b a b− + + 3 2 1x x = + 第 22 题图 接受问卷调查的学生人数扇形统计图 · · · 了解 基本了解 了解很少 不了解 50% 接受问卷调查的学生人数折线统计图 了解 程度 学生人数 5 10 15 20 25 30 不了解 了解很少 基本了解 了解 23．（本题满分 10 分） 如 图 所 示 , 在 梯 形 中 , ∥ , , 为 上 一 点 , . (1) 求证: ； (2) 若 ,试判断四边形 的形状,并说明理由． 24．（本题满分 10 分） 如图所示,当小华站立在镜子 前 处时, 他看自己的脚在镜中的像的俯角为 ；如 果小华向后退 0.5 米到 处,这时他看自己的脚在镜中的像的俯角为 .求小华的眼睛 到地面的距离.(结果精确到 0.1 米,参考数 据: ) 25．（本题满分 10 分） 如图①所示,已知 、 为直线 上两点,点 为直线 上方一动点,连接 、 ,分 别以 、 为边向 外作正方形 和正方形 ,过点 作 于点 ,过点 作 于点 . (1)如图②,当点 恰好在直线 上时(此时 与 重合),试说明 ； (2)在图①中,当 、 两点都在直线 的上方时,试探求三条线段 、 、 之 间的数量关系,并说明理由； (3)如图③,当点 在直线 的下方时,请直接写出三条线段 、 、 之间的数 量关系.(不需要证明) ABCD AD BC 90BDC∠ = ° E BC BDE DBC∠ = ∠ DE EC= 1 2AD BC= ABED EF A 45° B 30° 3 1.73≈ A B l C l AC BC AC BC ABC∆ CADF CBEG D 1DD l⊥ 1D E 1EE l⊥ 1E E l 1E E 1DD AB= D E l 1DD 1EE AB E l 1DD 1EE AB 第 23 题图 A B C D E 图②图① 第 25 题图 l(E1)A B C D F G E D1 图③ lE1 A B C D F G ED1 lE1A B C D F G E D1 第 24 题图 F EAB B1A1 CD 30º 45º 26．（本题满分 10 分） 如图所示, , , ,点 是以 为直径的半圆 上一动点, 交直线 于点 ,设 . (1)当 时,求 的长； (2)当 时,求线段 的长； (3)若要使点 在线段 的延长线上,则 的取值范围是_________.(直接写出答案) 27．（本题满分 12 分） 知识迁移 当 且 时 ， 因 为 ≥ , 所 以 ≥ , 从而 ≥ (当 时取等号). 记函数 ,由上述结论可知：当 时,该函数有最小 值为 .[来源:Z_xx_k.Com] 直接应用 已知函数 与函数 , 则当 _________时, 取得 最小值为_________. 变形应用 已知函数 与函数 ,求 的最小值,并指 出取得该最小值时相应的 的值. 实际应用 已知某汽车的一次运输成本包含以下三个部分：一是固定费用,共 元；二是燃 油费,每千米为 元；三是折旧费,它与路程的平方成正比,比例系数为 .设该汽 车一次运输的路程为 千米,求当 为多少时,该汽车平均每千米的运输成本最低？最 低是多少元？ AC AB⊥ 2 3AB = 2AC = D AB O DE CD⊥ AB E (0 90 )DAB α α∠ = ° < < ° 18α = ° BD 30α = ° BE E BA α 0a > 0x > 2( )ax x − 0 2 ax a x − + 0 ax x + 2 a x a= ( 0, 0)ay x a xx = + > > x a= 2 a 1 ( 0)y x x= > 2 1 ( 0)y xx = > x = 1 2y y+ 1 1( 1)y x x= + > − 2 2 ( 1) 4( 1)y x x= + + > − 2 1 y y x 360 1.6 0.001 x x C A B D · 第 26 题图 EO ┐ α 28．（本题满分 12 分） 在平面直角坐标系 中,已知二次函数 的图象经过点 和点 ,直线 经过抛物线的顶点且与 轴垂直,垂足为 . (1) 求该二次函数的表达式； (2) 设抛物线上有一动点 从点 处出发沿抛物线向上运动,其纵坐标 随时间 ≥ )的变化规律为 .现以线段 为直径作 . ①当点 在起始位置点 处时,试判断直线 与 的位置关系,并说明理由；在点 运动的过程中,直线 与 是否始终保持这种位置关系? 请说明你的理由； ②若在点 开始运动的同时,直线 也向上平行移动,且垂足 的纵坐标 随时间 的变化规律为 ,则当 在什么范围内变化时,直线 与 相交? 此时, 若直线 被 所截得的弦长为 ,试求 的最大值. xOy 21 4y x mx n= + + (2,0)A 3(1, )4B − l y Q P B 1y (t t 0 1 3 24y t= − + OP C P B l C P l C P l Q 2y t 2 1 3y t= − + t l C l C a 2a 第 28 题备用图 · ABO 1 2 x y lQ 第 28 题图 · ABO 1 2 x y [来源:Z。xx。k.Com]绝密★启用前 盐城市二○一二年初中毕业与升学统一考试 数学试题参考答案 一、选择题（每小题 3 分，共 24 分） 题号 1[来源:学*科*网 Z*X*X*K] 2 3 4 5 6 7 8 答案 D C C A B D C B 二、填空题（每小 题 3 分，共 30 分） 9． ≥－1 10． 11． 12．2 13． 14． 15． （或 或 ）（说明：答案有三类:一是一个内角为直 角；二是相邻两角相等；三是对角互补） 16．80 17．0 或 2 18．14 三、解答题 19．(1)解：原式 …………………………………………………………………3 分 …………………………………… ……………………………………4 分 (2)解 ：原式 ……………………………………………………2 分 ………………………………………………………………………4 分 20．解： ………………………………………………………………………3 分 解之得: …………………………………………………………………………6 分 检验: 当 时, , ∴ 是原方程的解…………………………8 分 21．解：解法一: 列表（如下表所示）………………………………………………………5 分 ∴共有 9 种等可能的结果,P(第二次抽取的数字大于第一次抽取的数字)= ． ……8 分 解法二:画树状图(如图所示): x ( 2 )( 2 )a b a b+ − 78.03 10× 1 2 4y x = − 90A∠ = ° A B∠ = ∠ 180A C∠ + ∠ = ° 1 112 2 = − − 1= − 2 2 22 2a ab b ab b= − + + + 2 22a b= + 3( 1) 2x x+ = 3x = − 3x = − ( 1) 0x x + ≠ 3x = − 1 3 1 2 3 1 2 3 1 2 3 1 2 3 第二次 第一次 开始 1 2 3 1 (1,1) (1,2) (1,3) 2 (2,1) (2,2) (2,3) 3 (3,1) (3,2) (3,3) 结果 第一次 第二次 所有可能的结果：(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3) ……5 分 ∴共有 9 种等可能的结果,P(第二次抽取的数字大于第一次抽取的数字)= ． ………8 分 22．解：(1)60 …………………………2 分 (2)补全折线图(如图所示)……………4 分 “基本了解”部分所对应扇形的圆心角 的大小为 …………6 分 （3）估计这两部分的总人数 为 （名）……8 分 23．解：（1）∵ ,∴ ,且 ……2 分 又∵ ,∴ ……………………………………………4 分 ∴ ………………………………………………………………………………5 分 （2）四边形 为菱形………………………………………………………………… 6 分 ∵ ,∴ ,∵ ,∴ ……………7 分 ∵ ,∴ ……………………………………………………………8 分 又∵ ∥ , ∴四边形 为平行四边形………………………………………9 分 又∵ ,∴ 为菱形 ……………………………………………………10 分 (说明:其它解法,仿此得分) 24．解：设 ，则在 中，∵ , ∴ ……3 分 又在 中，∵ ,∴ ……………………5 分 ∴ ………………………………………………………………………………6 分 由对称性知： ， ，∴ ,即 ……………8 分 解得 ,∴小华的眼睛到地面的距离约为 ……………………10 分 (说明:未写答的,不扣分；其它解法，仿此得分) 1 3 15 360 9060 × ° = ° 5 151200 40060 +× = 90BDC∠ = ° 90BDE EDC∠ + ∠ = ° 90DBC C∠ + ∠ = ° BDE DBC∠ = ∠ EDC C∠ = ∠ DE EC= ABED BDE DBC∠ = ∠ BE DE= DE EC= 1 2BE EC BC= = 1 2AD BC= AD BE= AD BC ABED BE DE= ABED ( )AC x m= 1Rt CAA∆ 1 45CA A∠ = ° 1AC AA x= = 1Rt DB B∆ 1 30DB B∠ = ° 1 1 3tan 3 DBDB B BB ∠ = = 1 3BB x= 1AE A E= 1BE B E= 1 1 1BB AA= + 3 1x x= + 3 1 1.42x += ≈ 1.4( )m 第 22 题图 · 接受问卷调查的学生人数折线统计图 了解 程度 学生人数 5 10 15 20 25 30 不了解 了解很少 基本了解 了解 25．解：（1）在正方形 中,∵ ， ， ∴ ………………………………………………………………1 分 又∵ , ∴ ,∴ , ∴ ……………………………………………………………………2 分 又∵四边形 为正方形,∴ ,∴ ……3 分 在 与 中, , ∴ ≌ ,∴ ………………4 分 （2） ……………………………5 分 过点 作 ，垂足为 ， 由（1）知： ≌ ， ≌ ……………………………………6 分 ∴ , ,∴ ………………………8 分 （3） …………………………………………………………………10 分 (说明:其它解法,仿此得分) 26．解: (1)连接 ,在⊙ 中，∵ ,∴ ………2 分 又∵ ,∴ ……………………………………………4 分 (2)∵ 为⊙ 的直径,∴ ,又∵ , , ∴ ， ……………………………………………………5 分 又∵ , ∴ , ∴ , 又∵ , ∴ ,∴ ………………………6 分 又∵ ,∴ ,∴ , 又∵ ,∴ ,∴ ∽ ……………7 分 ∴ ,又∵ , ∴ ,∴ ………………………8 分 （3） ＜ ＜ ………………………………………………………………………10 分 (说明:其它解法,仿此得分) ACFD AC AD= 90CAD∠ = ° 1 90DAD CAB∠ + ∠ = ° 1DD l⊥ 1 90DD A∠ = ° 1 1 90D DA DAD∠ + ∠ = ° 1CAB D DA∠ = ∠ BCGE 90ABC CBE∠ = ∠ = ° 1ABC DD A∠ = ∠ 1ADD∆ CAB∆ 1 1 ABC DD A CAB ADD AC DA ∠ = ∠ ∠ = ∠  = 1ADD∆ CAB∆ 1DD AB= 1 1DD EE AB+ = C CH l⊥ H 1ADD∆ CAH∆ 1BEE∆ CBH∆ 1DD AH= 1EE BH= 1 1DD EE AH BH AB+ = + = 1 1DD EE AB− = OD O 18DAB∠ = ° 2 36DOB DAB∠ = ∠ = ° 2 3AB =  36 3 3 180 5BDl π π×= = AB O 90ADB∠ = ° 30DAB∠ = ° 2 3AB = 3BD = cos30 3AD AB= ⋅ ° = AC AB⊥ 90CAB∠ = ° 90CAD DAB∠ + ∠ = ° 90ADB∠ = ° 90DAB B∠ + ∠ = ° CAD B∠ = ∠ DE CD⊥ 90CDE∠ = ° 90CDA ADE∠ + ∠ = ° 90ADE EDB∠ + ∠ = ° CDA EDB∠ = ∠ CDA∆ EDB∆ AC AD BE BD = 2AC = 2 3 3BE = 2 3 3BE = 60° α 90° H E1A B C D F G E D1 27. 解：直接应用 1, 2 ……………………………………………………………………………(每空 1 分) 2 分 变形应用 解：∵ ………………………………………3 分 ∴ 有最小值为 , ……………………………………………………………4 分 当 ,即 时取得该最小值…………………………………………………6 分 实际应用 解：设该汽车平均每千米的运输成本为 元,则 ………… 9 分 , …………………………………10 分 ∴当 (千米)时, 该汽车平均每千米的运输成本 最低………11 分 最低成本为 元. ………………………………………12 分 28．解：（1）将点 和点 的坐标代入,得 ,解得 , ∴二次函数的表达式为 ……………………………………………………3 分 (2)①当点 在点 处时,直线 与 相切,理由如下: ∵点 ,∴圆心的坐标为 ,∴ 的半径为 , 又抛物线的顶点坐标为(0,－1),即直线 l 上所有点的纵坐标均为－1,从而圆心 C 到直 线 l 的距离为 ,∴直线 与 相切. …………………… 5 分 在点 运动的过程中,直线 与 始终保持相切的位置关系,理由如下: 方法一: 设点 ,则圆心的坐标为 ,∴圆心 C 到直线 l 的距离 为 ,又∵ ,∴ ,则 的半 径为 ,[来源:Zxxk.Com] ∴直线 与 始终相切. ………………………………………………………… 7 分 方法二: 设点 ≥1),则圆心的坐标为 ,∴ 的半径为 2 2 1 ( 1) 4 4( 1) ( 1)1 1 y x x xy x x + += = + + > −+ + 2 1 y y 2 4 4= 1 4x + = 1x = y 20.001 1.6 360x xy x + += 360 3600000.001 1.6 0.001( ) 1.6x xx x = + + = + + 360000 600x = = y 0.001 2 360000 1.6 2.8× + = (2,0)A 3(1, )4B − 1 2 0 1 3 4 4 m n m n + + = + + = − 0 1 m n =  = − 21 14y x= − P B l C 3(1, )4P − 1 3( , )2 8C − C 2 21 3 5( ) | |2 8 8r = + − = 3 5( 1)8 8d r= − − − = = l C P l C 0 3( , 2 )4P x t− + 0 3( , )2 8 xC t− + 3 5( ) ( 1)8 8d t t= − + − − = + 2 0 3 12 14 4t x− + = − 2 0 8 1x t= + C 2 2 2 20 3 8 1 3 9 5 5( ) | | ( )2 8 4 4 64 8 8 x tr t t t t t d += + − + = + − + = + = + = l C 2 0 0 0 1( , 1)(4P x x x− 20 0 1 1( , )2 8 2 xC x − C , 而 圆 心 C 到 直 线 l 的 距 离 为 ,∴直线 与 始终相切.…………………… 7 分 ②由①知,圆 C 的半径为 . 又∵圆心 C 的纵坐标为 ,直线 l 上的点的纵坐标为 ,所以 ( ⅰ ) 当 ≥ , 即 ≤ 时 , 圆 心 C 到 直 线 l 的 距 离 为 ,则由 ,得 ,解得 , ∴此时 ≤ ； ……………………………………………………………………8 分 ( ⅱ ) 当 ＜ , 即 ＞ 时 , 圆 心 C 到 直 线 l 的 距 离 为 ,则由 ,得 ,解得 , ∴此时 ＜ ； 综上所述,当 时,直线 与 相交. ………………………………………9 分 (说明: 若学生就写成 ≤ 或 ＜ ,得全分；若学生依据直观,只考虑圆心 C 在直线 l 下方的情况,解出 后,就得 ,也给全分) ∵当 时,圆心 C 到直线 l 的距离为 ,又半径为 , ∴ , ……………………11 分 ∴当 时, 取得最大值为 .…………………………………………………1 2 2 2 2 2 20 0 0 0 1 1 1 1 1 1( ) | | ( )2 8 2 8 2 8 2 xr x x x= + − = + = + 2 2 0 0 1 1 1 1( 1)8 2 8 2d x x r= − − − = + = l C 5 8r t= + 3 8 t− + 1 3t− + 3 8 t− + 1 3t− + t 5 16 3 5( ) ( 1 3 ) 28 8d t t t= − + − − + = − d r< 5 528 8t t− < + 0t > 0 t< 5 16 3 8 t− + 1 3t− + t 5 16 3 5( 1 3 ) ( ) 28 8d t t t= − + − − + = − d r< 5 52 8 8t t− < + 5 4t < 5 16 5 4t < 50 4t< < l C 0 t< 5 16 5 16 5 4t < 5 4t < 50 4t< < 50 4t< < 5| 2 |8d t= − 5 8r t= + 2 2 2 2 2 25 54( ) 4[( ) | 2 | ] 12 158 8a r d t t t t= − = + − − = − + 5 8t = 2a 75 16