四川省自贡市2017年中考数学试题 7页

四川省自贡市初2017届毕业生学业考试数学试卷 一、选择题（每小题4分，共48分）‎ ‎1．计算（－1）2017的结果是（ ）‎ ‎ A．－1 B．‎1 ‎‎ C．－2017 D．2017‎ ‎2．下列成语所描述的事件为随机事件的是（ ）‎ ‎ A．水涨船高 B．守株待兔 C．水中捞月 D．缘木求鱼 ‎3．380亿用科学记数法表示为（ ）‎ ‎ A．38×109 B．0.38×‎1013 ‎‎ C．3.8×1011 D．3.8×1010‎ ‎≤‎ ‎4．不等式组 的解集在数轴上表示正确的是（ ）‎ ‎ A．B． C． D．‎ ‎5．如图，直线a∥b，点B在直线a上，且AB⊥BC，∠1＝35°，那么∠2＝（ ）‎ ‎ A．45° B．50° C．55° D．60°‎ ‎6．下列图形中，是轴对称图形，但不是中心对称图形的是（ ）‎ A． B． C． D． ‎ ‎7．对于一组统计数据3，3，6，5，3．下列说法错误的是（ ）‎ ‎ A．众数是3 B．平均数是‎4 C．方差是1.6 D．中位数是6‎ ‎8．下列几何体中，主视图是矩形的是（ ）‎ A． B． C． D． ‎ ‎9．下列四个命题中，其正确命题的个数是（ ）‎ ‎①若a＞b，则； ②垂直于弦的直径平分弦；‎ ‎③平行四边形的对角线互相平分； ④反比例函数，当k＜0时y随x的增大而增大．‎ A．1 B．‎2 C．3 D．4‎ ‎10．如图，AB是⊙O的直径，PA切⊙O于点A，PO交⊙O于点C，连接BC，若∠P＝40°，则∠B等于（ ）‎ A．20° ‎ B．25°‎ C．30°‎ D．40°‎ ‎11．填在下面各正方形中的四个数之间都有相同的规律，根据这种规律m的值为（ ）‎ A．180 B．‎182 C．184 D．186‎ ‎12．一次函数和反比例函数（）的图象如图所示，若，则x的取值范围是（ ） ‎ A．－2＜x＜0或x＞1 ‎ B．－2＜x＜1 ‎ C．x＜－2或x＞1 ‎ D．x＜－2或0＜x＜1‎ 二、填空题（每小题4分，共24分）‎ ‎13．计算：＝ ．‎ ‎14．如图，在△ABC中，MN∥BC，分别交AB、AC于点M、N，‎ 若AM＝1，MB＝2，BC＝3，则MN的长为 ．‎ ‎15．我国明代数学家程大位的名著《直接算法统宗》里有一道著名算题：‎ ‎“一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？”‎ 意思是：有100个和尚分100个馒头，正好分完，如果大和尚一人分3个，小和尚3人分一个，试问大、小和尚和有几人？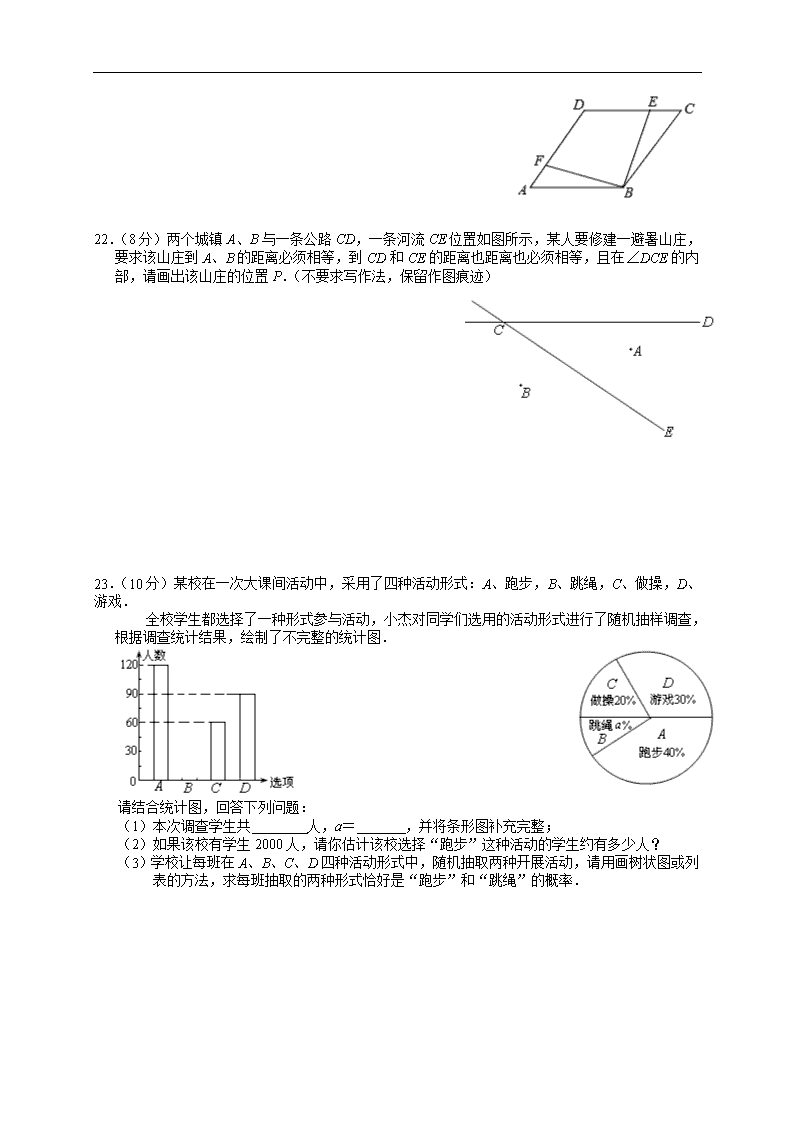设大、小和尚各有x、y人，则可列方程组 ．‎ ‎16．圆锥底面圆的周长为6πcm，高为‎4cm，则该圆锥的全面积是 ；侧面展开扇形的圆心角的度数是 ．‎ ‎17．如图，等腰△ABC内接于⊙O，已知AB＝AC，∠ABC＝30°，‎ BD是⊙O的直径，如果CD＝，则AD＝ ．‎ ‎18．如图，13个边长为1的小正方形，排列形式如图，把它们分割，使分割后能形成 一个大的正方形．请在如图所示的网格(网格边长为1)中，用直尺作出这个大正方形．‎ 三、解答题（共8个题，共78分）‎ ‎19．（8分）计算：‎ ‎20．（8分）先化简，再求值：，其中a＝2．‎ ‎21．（8分）如图，点E、F分别在菱形ABCD的边DC、DA上，且CE＝AF．求证：∠ABF＝∠CBE．‎ ‎22．（8分）两个城镇A、B与一条公路CD，一条河流CE位置如图所示，某人要修建一避暑山庄，要求该山庄到A、B的距离必须相等，到CD和CE的距离也距离也必须相等，且在∠DCE的内部，请画出该山庄的位置P．（不要求写作法，保留作图痕迹）‎ ‎23．（10分）某校在一次大课间活动中，采用了四种活动形式：A、跑步，B、跳绳，C、做操，D、游戏．‎ 全校学生都选择了一种形式参与活动，小杰对同学们选用的活动形式进行了随机抽样调查，根据调查统计结果，绘制了不完整的统计图．‎ 请结合统计图，回答下列问题：‎ ‎（1）本次调查学生共 人，a＝ ，并将条形图补充完整；‎ ‎（2）如果该校有学生2000人，请你估计该校选择“跑步”这种活动的学生约有多少人？‎ ‎（3）学校让每班在A、B、C、D四种活动形式中，随机抽取两种开展活动，请用画树状图或列表的方法，求每班抽取的两种形式恰好是“跑步”和“跳绳”的概率．‎ ‎24．（10分）[探究函数的图象与性质]‎ ‎（1）函数的自变量x的取值范围是 ；‎ ‎（2）下列四个函数图象中可能是函数的图象是 ；‎ ‎（3）对于函数，当x＞0时，求y的取值范围．‎ 解：∵x＞0，∴ ‎ ‎∵≥0，∴y≥ ．‎ ‎[拓展运用]‎ ‎（4）若函数，则y的取值范围是 ．‎ ‎25．（12分）如图1，在平面直角坐标系中，O为坐标原点，点A(－1，0)，点B(0，)．‎ ‎ （1）求∠BAO的度数；‎ ‎（2）如图1，将△AOB绕点O顺时针旋转得△A′OB′，当点A′恰好落在AB边上时，设△AB′O的面积为S2，S1与S2有何关系？为什么？‎ ‎（3）若将△AOB绕点O顺时针旋转到如图2所示的位置时，S1与S2的关系发生变化了吗？证明你的判断．‎ ‎ ‎ ‎ 图1 图2‎ ‎26．（14分）抛物线y＝4x2－2ax＋b与x轴相交于A(x1，0)，B(x2，0)，（0＜x1＜x2）两点，与y轴相交于点C．‎ ‎（1）设AB＝2，tan∠ABC＝4，求抛物线的解析式；‎ ‎（2）在（1）中，若D为直线BC下方抛物线上一动点，当△BCD的面积最大时，求点D的坐标；‎ ‎（3）是否存在整数a、b使1＜x1＜2和1＜x2＜2同时成立，请证明你的结论．‎ 四川省自贡市初2017届毕业生学业考试数学答案 一、1．A；2．B；3．D；4．C；5．C；6．A；7．D；8．A；9．B；10．B；11．C；12．D．‎ 二、13．2；14．1；15．；16．24π，216°；17．4；18．‎ 三、19．解：原式＝‎ ‎20．解：原式＝‎ ‎∵a＝2 ∴原式＝‎ ‎21．证明：∵四边形ABCD是菱形 ‎ ∴∠A＝∠C，AB＝BC ‎ 又∵CE＝AF ‎ ∴△ABF≌△CBE（SAS）‎ ‎∴∠ABF＝∠CBE．‎ ‎22．解：如图，作线段AB的中垂线与∠DCE的平分线交于点P，点P即为所求．‎ ‎23．解：（1）300，10．‎ ‎ （2）2000×40%＝800‎ ‎∴估计该校选择“跑步”这种活动的学生约有800人．‎ ‎（3）画树状图为：‎ ‎ 由树状图可知：每班抽取的两种形式恰好是“跑步”和“跳绳”的概率＝‎ ‎24．（1）x≠0；（2）C；（3）4，4；（4）y≥1．‎ ‎25．（1）∵A（－1，0），B（0，），∠AOB＝90°‎ ‎ ∴，∴∠BAO＝60°‎ ‎ （2）S1＝S2，理由如下：‎ ‎ 依题意有：A′A＝A′O，∠BAO＝60°，‎ ‎ ∴△A′AO是等边三角形，‎ ‎∴∠AOA′＝∠BA′O＝60°，‎ ‎ ∴A′B′∥x轴，∴点A′、B′到x轴的距离相等，‎ ‎ ∵∠ABO＝∠A′OB＝90°－60°＝30°‎ ‎∴A′O＝A′B′ ∴AO＝A′B′‎ ‎ ∵等边△A′AO的三条高都相等 ‎ ∴点O到AB的距离等于点B′到x轴的距离 ∴S1＝S2（等底等高的三角形面积相等）‎ ‎（3）S1与S2的关系没变，仍然有S1＝S2，理由如下：‎ 过点B作BC⊥AO于C，过点B′作B′D⊥x轴于D，‎ ‎ ∴∠BCO＝∠B′DO＝90°‎ 依题意有：∠BOD＝∠A′OB′＝90°，B′O＝BO，A′O＝AO，‎ ‎ ∴∠1＋∠A′OD＝∠2＋∠A′OD＝90°‎ ‎ ∴∠1＝∠2‎ ‎ ∴△BOC≌△B′OD（AAS）‎ ‎ ∴BC＝B′D 又∵AO＝A′O ‎ ∴S1＝S2（等底等高的三角形面积相等）‎ ‎26．抛物线y＝4x2－2ax＋b与x轴相交于A(x1，0)，B(x2，0)，（0＜x1＜x2）两点，与y轴相交于点C．‎ ‎（1）设AB＝2，tan∠ABC＝4，求抛物线的解析式；‎ ‎（2）在（1）中，若D为直线BC下方抛物线上一动点，当△BCD的面积最大时，求点D的坐标；‎ ‎（3）是否存在整数a、b使1＜x1＜2和1＜x2＜2同时成立，请证明你的结论．‎ 解：（1）依题意得： （3）依题意有：即：解得：‎ ‎ ∴ ∵a为整数 ∴a＝5，6，7 ‎ ‎ 又‎4a2－16b＞0①，4－‎2a＋b＞0②，16－‎4a＋b＞0③，b为整数④‎ ‎ 即：① ∴把a＝5代入①②③④解得b无解 ‎ ∵tan∠ABC＝4，∠BOC＝90° 把a＝6代入①②③④解得b无解 ‎ ∴，即 把a＝7代入①②③④解得b无解 ‎ ∵抛物线对称轴为，AB＝2 综上所述不存在整数a、b使1＜x1＜2和1＜x2＜2同时成立．‎ ‎ ∴‎ ‎ ∴②‎ 解由①②构成的方程组可得a＝－4或a＝8‎ 经检验只有a＝8才成立．‎ 把a＝8代入①后解得：b＝12‎ ‎∴抛物线解析式为y＝4x2－16x＋12‎ ‎（2）过D作DE∥y轴交BC于E，设D（x，y）‎ ‎ ∵y＝4x2－16x＋12 ∴D（x，4x2－16x＋12）‎ 在y＝4x2－16x＋12中，令x＝0，则y＝12 ∴C（0，12）‎ 令y＝0，则x1＝1，x2＝3 ∴A（1，0），B（3，0）‎ 设直线BC：y＝kx＋12，把B点代入得：3k＋12＝0，k＝－4‎ ‎∴直线BC：y＝－x＋12 ∴E（x，－x＋12）‎ ‎∴DE＝（－x＋12）－（4x2－16x＋12）＝－4x2＋12x ‎∴S△BCD＝即：‎ 当x＝时S有最大值为：S ∴D（，－3）‎ ‎ ‎ ‎ 沿滩中学——熊礼刚的参考答案