2018—2020年江苏省数学中考试题分类（9）——反比例函数（含解析） 43页

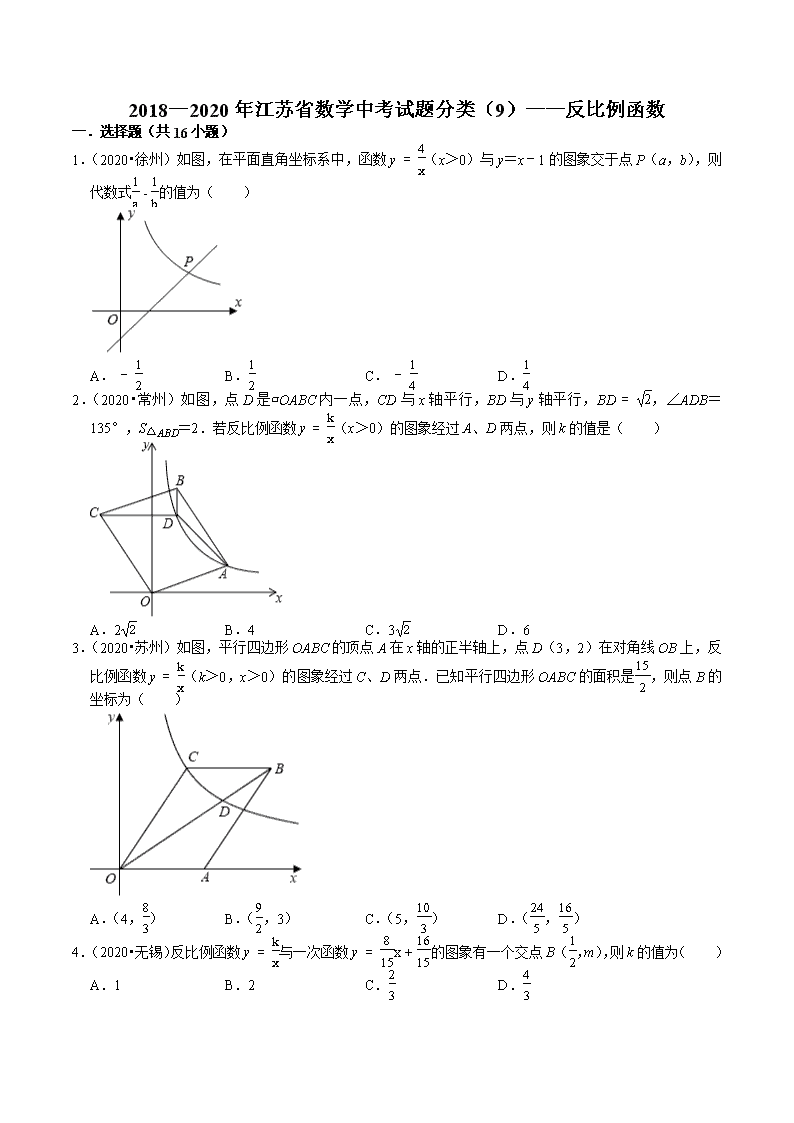
‎2018—2020年江苏省数学中考试题分类（9）——反比例函数 一．选择题（共16小题）‎ ‎1．（2020•徐州）如图，在平面直角坐标系中，函数y‎=‎‎4‎x（x＞0）与y＝x﹣1的图象交于点P（a，b），则代数式‎1‎a‎-‎‎1‎b的值为（　　）‎ A．‎-‎‎1‎‎2‎ B．‎1‎‎2‎ C．‎-‎‎1‎‎4‎ D．‎‎1‎‎4‎ ‎2．（2020•常州）如图，点D是▱OABC内一点，CD与x轴平行，BD与y轴平行，BD‎=‎‎2‎，∠ADB＝135°，S△ABD＝2．若反比例函数y‎=‎kx（x＞0）的图象经过A、D两点，则k的值是（　　）‎ A．2‎2‎ B．4 C．3‎2‎ D．6‎ ‎3．（2020•苏州）如图，平行四边形OABC的顶点A在x轴的正半轴上，点D（3，2）在对角线OB上，反比例函数y‎=‎kx（k＞0，x＞0）的图象经过C、D两点．已知平行四边形OABC的面积是‎15‎‎2‎，则点B的坐标为（　　）‎ A．（4，‎8‎‎3‎） B．（‎9‎‎2‎，3） C．（5，‎10‎‎3‎） D．（‎24‎‎5‎，‎16‎‎5‎）‎ ‎4．（2020•无锡）反比例函数y‎=‎kx与一次函数y‎=‎8‎‎15‎x+‎‎16‎‎15‎的图象有一个交点B（‎1‎‎2‎，m），则k的值为（　　）‎ A．1 B．2 C．‎2‎‎3‎ D．‎‎4‎‎3‎ ‎5．（2019•徐州）若A（x1，y1）、B（x2，y2）都在函数y‎=‎‎2019‎x的图象上，且x1＜0＜x2，则（　　）‎ A．y1＜y2 B．y1＝y2 C．y1＞y2 D．y1＝﹣y2‎ ‎6．（2019•淮安）当矩形面积一定时，下列图象中能表示它的长y和宽x之间函数关系的是（　　）‎ A． B． ‎ C． D．‎ ‎7．（2019•扬州）若反比例函数y‎=-‎‎2‎x的图象上有两个不同的点关于y轴的对称点都在一次函数y＝﹣x+m的图象上，则m的取值范围是（　　）‎ A．m＞2‎2‎ B．m＜﹣2‎2‎ ‎ C．m＞2‎2‎或m＜﹣2‎2‎ D．﹣2‎2‎‎＜‎m＜2‎‎2‎ ‎8．（2019•宿迁）如图，在平面直角坐标系xOy中，菱形ABCD的顶点A与原点O重合，顶点B落在x轴的正半轴上，对角线AC、BD交于点M，点D、M恰好都在反比例函数y‎=‎kx（x＞0）的图象上，则ACBD的值为（　　）‎ A．‎2‎ B．‎3‎ C．2 D．‎‎5‎ ‎9．（2019•无锡）如图，已知A为反比例函数y‎=‎kx（x＜0）的图象上一点，过点A作AB⊥y轴，垂足为B．若△OAB的面积为2，则k的值为（　　）‎ A．2 B．﹣2 C．4 D．﹣4‎ ‎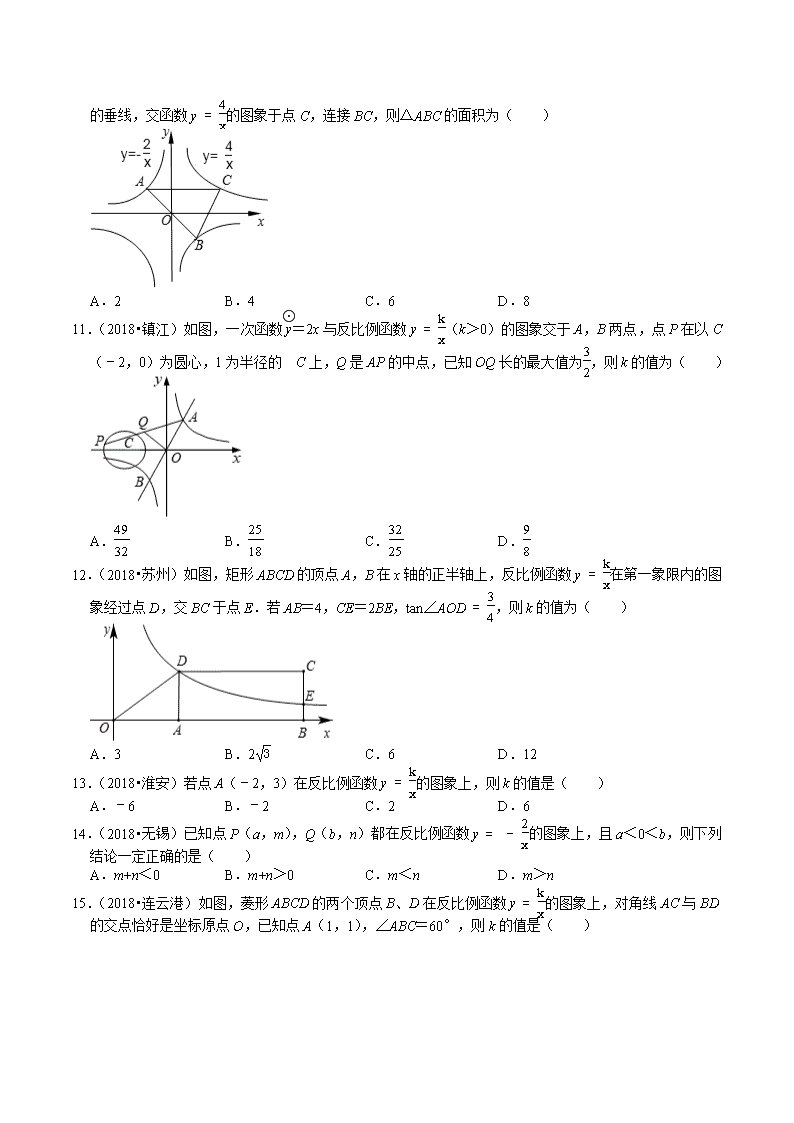10．（2018•徐州）如图，在平面直角坐标系中，函数y＝kx与y‎=-‎‎2‎x的图象交于A，B两点，过A作y 轴的垂线，交函数y‎=‎‎4‎x的图象于点C，连接BC，则△ABC的面积为（　　）‎ A．2 B．4 C．6 D．8‎ ‎11．（2018•镇江）如图，一次函数y＝2x与反比例函数y‎=‎kx（k＞0）的图象交于A，B两点，点P在以C（﹣2，0）为圆心，1为半径的⊙C上，Q是AP的中点，已知OQ长的最大值为‎3‎‎2‎，则k的值为（　　）‎ A．‎49‎‎32‎ B．‎25‎‎18‎ C．‎32‎‎25‎ D．‎‎9‎‎8‎ ‎12．（2018•苏州）如图，矩形ABCD的顶点A，B在x轴的正半轴上，反比例函数y‎=‎kx在第一象限内的图象经过点D，交BC于点E．若AB＝4，CE＝2BE，tan∠AOD‎=‎‎3‎‎4‎，则k的值为（　　）‎ A．3 B．2‎3‎ C．6 D．12‎ ‎13．（2018•淮安）若点A（﹣2，3）在反比例函数y‎=‎kx的图象上，则k的值是（　　）‎ A．﹣6 B．﹣2 C．2 D．6‎ ‎14．（2018•无锡）已知点P（a，m），Q（b，n）都在反比例函数y‎=-‎‎2‎x的图象上，且a＜0＜b，则下列结论一定正确的是（　　）‎ A．m+n＜0 B．m+n＞0 C．m＜n D．m＞n ‎15．（2018•连云港）如图，菱形ABCD的两个顶点B、D在反比例函数y‎=‎kx的图象上，对角线AC与BD的交点恰好是坐标原点O，已知点A（1，1），∠ABC＝60°，则k的值是（　　）‎ A．﹣5 B．﹣4 C．﹣3 D．﹣2‎ ‎16．（2018•扬州）已知点A（x1，3），B（x2，6）都在反比例函数y‎=-‎‎3‎x的图象上，则下列关系式一定正确的是（　　）‎ A．x1＜x2＜0 B．x1＜0＜x2 C．x2＜x1＜0 D．x2＜0＜x1‎ 二．填空题（共10小题）‎ ‎17．（2020•宿迁）如图，点A在反比例函数y‎=‎kx（x＞0）的图象上，点B在x轴负半轴上，直线AB交y轴于点C，若ACBC‎=‎‎1‎‎2‎，△AOB的面积为6，则k的值为　 　．‎ ‎18．（2020•南通）将双曲线y‎=‎‎3‎x向右平移1个单位长度，再向下平移2个单位长度，得到的新双曲线与直线y＝kx﹣2﹣k（k＞0）相交于两点，其中一个点的横坐标为a，另一个点的纵坐标为b，则（a﹣1）（b+2）＝　 　．‎ ‎19．（2020•淮安）如图，等腰△ABC的两个顶点A（﹣1，﹣4）、B（﹣4，﹣1）在反比例函数y‎=‎k‎1‎x（x＜0）的图象上，AC＝BC．过点C作边AB的垂线交反比例函数y‎=‎k‎1‎x（x＜0）的图象于点D，动点P从点D出发，沿射线CD方向运动3‎2‎个单位长度，到达反比例函数y‎=‎k‎2‎x（x＞0）图象上一点，则k2＝　 　．‎ ‎20．（2020•盐城）如图，已知点A（5，2）、B（5，4）、C（8，1）．直线l⊥x轴，垂足为点M（m，0）．其中m‎＜‎‎5‎‎2‎，若△A′B′C′与△ABC关于直线l对称，且△A′B′C′有两个顶点在函数y‎=‎kx（k≠0）的图象上，则k的值为　 　．‎ ‎21．（2020•泰州）如图，点P在反比例函数y‎=‎‎3‎x的图象上，且横坐标为1，过点P作两条坐标轴的平行线，与反比例函数y‎=‎kx（k＜0）的图象相交于点A、B，则直线AB与x轴所夹锐角的正切值为　 　．‎ ‎22．（2019•无锡）如图，A为反比例函数y‎=‎kx（k＜0）的图象上一点，AP⊥y轴，垂足为P．点B在直线AP上，且PB＝3PA，过点B作直线BC∥y轴，交反比例函数的图象于点C，若△PAC的面积为4，则k的值为　 　．‎ ‎23．（2019•南通）如图，过点C（3，4）的直线y＝2x+b交x轴于点A，∠ABC＝90°，AB＝CB，曲线y‎=‎kx ‎（x＞0）过点B，将点A沿y轴正方向平移a个单位长度恰好落在该曲线上，则a的值为　 　．‎ ‎24．（2019•镇江）已知点A（﹣2，y1）、B（﹣1，y2）都在反比例函数y‎=-‎‎2‎x的图象上，则y1　 　y2．（填“＞”或“＜”）‎ ‎25．（2019•无锡）某个函数具有性质：当x＞0时，y随x的增大而增大，这个函数的表达式可以是　 　（只要写出一个符合题意的答案即可）．‎ ‎26．（2018•无锡）已知点A、B都在反比例函数y‎=‎‎6‎x（x＞0）的图象上，其横坐标分别是m、n（m＜n）．过点A分别向x轴、y轴作垂线，垂足分别是C、D；过点B分别向x轴、y轴作垂线，垂足分别是E、F，AC与BF交于点P．当点P在线段DE上、且m（n﹣2）＝3时，m的值等于　 　．‎ 三．解答题（共16小题）‎ ‎27．（2020•镇江）如图，正比例函数y＝kx（k≠0）的图象与反比例函数y‎=-‎‎8‎x的图象交于点A（n，2）和点B．‎ ‎（1）n＝　 　，k＝　 　；‎ ‎（2）点C在y轴正半轴上．∠ACB＝90°，求点C的坐标；‎ ‎（3）点P（m，0）在x轴上，∠APB为锐角，直接写出m的取值范围．‎ ‎28．（2020•常州）如图，正比例函数y＝kx的图象与反比例函数y‎=‎‎8‎x（x＞0）的图象交于点A（a，4）．点B为x轴正半轴上一点，过B作x轴的垂线交反比例函数的图象于点C，交正比例函数的图象于点D．‎ ‎（1）求a的值及正比例函数y＝kx的表达式；‎ ‎（2）若BD＝10，求△ACD的面积．‎ ‎29．（2020•徐州）如图，在平面直角坐标系中，一次函数y＝kx+b的图象经过点A（0，﹣4）、B（2，0），交反比例函数y‎=‎mx（x＞0）的图象于点C（3，a），点P在反比例函数的图象上，横坐标为n（0＜n＜3），PQ∥y轴交直线AB于点Q，D是y轴上任意一点，连接PD、QD．‎ ‎（1）求一次函数和反比例函数的表达式；‎ ‎（2）求△DPQ面积的最大值．‎ ‎30．（2020•扬州）如图，已知点A（1，2）、B（5，n）（n＞0），点P为线段AB上的一个动点，反比例函数y‎=‎kx（x＞0）的图象经过点P．小明说：“点P从点A运动至点B的过程中，k值逐渐增大，当点P在点A位置时k值最小，在点B位置时k值最大．”‎ ‎（1）当n＝1时．‎ ‎①求线段AB所在直线的函数表达式．‎ ‎②你完全同意小明的说法吗？若完全同意，请说明理由；若不完全同意，也请说明理由，并求出正确的k的最小值和最大值．‎ ‎（2）若小明的说法完全正确，求n的取值范围．‎ ‎31．（2020•南京）已知反比例函数y‎=‎kx的图象经过点（﹣2，﹣1）．‎ ‎（1）求k的值．‎ ‎（2）完成下面的解答．‎ 解不等式组‎2-x＞1，①‎kx‎＞1．②‎ 解：解不等式①，得　 　．‎ 根据函数y‎=‎kx的图象，得不等式②的解集　 　．‎ 把不等式①和②的解集在数轴上表示出来．‎ 从图中可以找出两个不等式解集的公共部分，得不等式组的解集　 　．‎ ‎32．（2020•连云港）如图，在平面直角坐标系xOy中，反比例函数y‎=‎mx（x＞0）的图象经过点A（4，‎3‎‎2‎），点B在y轴的负半轴上，AB交x轴于点C，C为线段AB的中点．‎ ‎（1）m＝　 　，点C的坐标为　 　；‎ ‎（2）若点D为线段AB上的一个动点，过点D作DE∥y轴，交反比例函数图象于点E，求△ODE面积的最大值．‎ ‎33．（2019•无锡）如图，一次函数y＝x+3的图象与反比例函数y‎=‎kx（x＞0）的图象相交于点A（1，m），与x轴相交于点B．‎ ‎（1）求这个反比例函数的表达式；‎ ‎（2）C为反比例函数的图象上异于点A的一点，直线AC交x轴于点D，设直线AC所对应的函数表达式为y＝nx+b．‎ ‎①若△ABD的面积为12，求n、b的值；‎ ‎②作CE⊥x轴，垂足为E，记t＝OE•DE，求n•t的值．‎ ‎34．（2019•徐州）如图，平面直角坐标系中，O为原点，点A、B分别在y轴、x轴的正半轴上．△AOB的两条外角平分线交于点P，P在反比例函数y‎=‎‎9‎x的图象上．PA的延长线交x轴于点C，PB的延长线交y轴于点D，连接CD．‎ ‎（1）求∠P的度数及点P的坐标；‎ ‎（2）求△OCD的面积；‎ ‎（3）△AOB的面积是否存在最大值？若存在，求出最大面积；若不存在，请说明理由．‎ ‎35．（2019•镇江）如图，点A（2，n）和点D是反比例函数y‎=‎mx（m＞0，x＞0）图象上的两点，一次函数y＝kx+3（k≠0）的图象经过点A，与y轴交于点B，与x轴交于点C，过点D作DE⊥x轴，垂足为E，连接OA，OD．已知△OAB与△ODE的面积满足S△OAB：S△ODE＝3：4．‎ ‎（1）S△OAB＝　 　，m＝　 　；‎ ‎（2）已知点P（6，0）在线段OE上，当∠PDE＝∠CBO时，求点D的坐标．‎ ‎36．（2019•常州）如图，在▱OABC中，OA＝2‎2‎，∠AOC＝45°，点C在y轴上，点D是BC的中点，反比例函数y‎=‎kx（x＞0）的图象经过点A、D．‎ ‎（1）求k的值；‎ ‎（2）求点D的坐标．‎ ‎37．（2019•苏州）如图，A为反比例函数y‎=‎kx（其中x＞0）图象上的一点，在x轴正半轴上有一点B，OB＝4．连接OA，AB，且OA＝AB＝2‎10‎．‎ ‎（1）求k的值；‎ ‎（2）过点B作BC⊥OB，交反比例函数y‎=‎kx（其中x＞0）的图象于点C，连接OC交AB于点D，求ADDB的值．‎ ‎38．（2019•宿迁）如图，一次函数y＝kx+b的图象与反比例函数y‎=-‎‎5‎x的图象相交于点A（﹣1，m）、B（n，﹣1）两点．‎ ‎（1）求一次函数表达式；‎ ‎（2）求△AOB的面积．‎ ‎39．（2019•泰州）已知一次函数y1＝kx+n（n＜0）和反比例函数y2‎=‎mx（m＞0，x＞0）．‎ ‎（1）如图1，若n＝﹣2，且函数y1、y2的图象都经过点A（3，4）．‎ ‎①求m，k的值；‎ ‎②直接写出当y1＞y2时x的范围；‎ ‎（2）如图2，过点P（1，0）作y轴的平行线l与函数y2的图象相交于点B，与反比例函数y3‎=‎nx（x＞0）的图象相交于点C．‎ ‎①若k＝2，直线l与函数y1的图象相交点D．当点B、C、D中的一点到另外两点的距离相等时，求m﹣n的值；‎ ‎②过点B作x轴的平行线与函数y1的图象相交于点E．当m﹣n的值取不大于1的任意实数时，点B、C间的距离与点B、E间的距离之和d始终是一个定值．求此时k的值及定值d．‎ ‎40．（2019•连云港）如图，在平面直角坐标系xOy中，函数y＝﹣x+b的图象与函数y‎=‎kx（x＜0）的图象相交于点A（﹣1，6），并与x轴交于点C．点D是线段AC上一点，△ODC与△OAC的面积比为2：3．‎ ‎（1）k＝　 　，b＝　 　；‎ ‎（2）求点D的坐标；‎ ‎（3）若将△ODC绕点O逆时针旋转，得到△OD'C'，其中点D'落在x轴负半轴上，判断点C'‎ 是否落在函数y‎=‎kx（x＜0）的图象上，并说明理由．‎ ‎41．（2019•盐城）如图，一次函数y＝x+1的图象交y轴于点A，与反比例函数y‎=‎kx（x＞0）的图象交于点B（m，2）．‎ ‎（1）求反比例函数的表达式；‎ ‎（2）求△AOB的面积．‎ ‎42．（2019•泰安）已知一次函数y＝kx+b的图象与反比例函数y‎=‎mx的图象交于点A，与x轴交于点B（5，0），若OB＝AB，且S△OAB‎=‎‎15‎‎2‎．‎ ‎（1）求反比例函数与一次函数的表达式；‎ ‎（2）若点P为x轴上一点，△ABP是等腰三角形，求点P的坐标．‎ ‎2018—2020年江苏省数学中考试题分类（9）——反比例函数 一．选择题（共16小题）‎ ‎1．（2020•徐州）如图，在平面直角坐标系中，函数y‎=‎‎4‎x（x＞0）与y＝x﹣1的图象交于点P（a，b），则代数式‎1‎a‎-‎‎1‎b的值为（　　）‎ A．‎-‎‎1‎‎2‎ B．‎1‎‎2‎ C．‎-‎‎1‎‎4‎ D．‎‎1‎‎4‎ ‎【答案】C ‎【解答】解：‎ 法一：由题意得，‎ y=‎‎4‎xy=x-1‎‎，解得，x=‎‎1+‎‎17‎‎2‎y=‎‎17‎‎-1‎‎2‎或x=‎‎1-‎‎17‎‎2‎y=‎‎-1-‎‎17‎‎2‎（舍去），‎ ‎∴点P（‎1+‎‎17‎‎2‎，‎17‎‎-1‎‎2‎），‎ 即：a‎=‎‎1+‎‎17‎‎2‎，b‎=‎‎17‎‎-1‎‎2‎，‎ ‎∴‎1‎a‎-‎1‎b=‎2‎‎1+‎‎17‎-‎2‎‎17‎‎-1‎=-‎‎1‎‎4‎；‎ 法二：由题意得，‎ 函数y‎=‎‎4‎x（x＞0）与y＝x﹣1的图象交于点P（a，b），‎ ‎∴ab＝4，b＝a﹣1，‎ ‎∴‎1‎a‎-‎1‎b=b-aab=-‎‎1‎‎4‎；‎ 故选：C．‎ ‎2．（2020•常州）如图，点D是▱OABC内一点，CD与x轴平行，BD与y轴平行，BD‎=‎‎2‎，∠ADB＝135°，S△ABD＝2．若反比例函数y‎=‎kx（x＞0）的图象经过A、D两点，则k的值是（　　）‎ A．2‎2‎ B．4 C．3‎2‎ D．6‎ ‎【答案】D ‎【解答】解：作AM⊥y轴于M，延长BD，交AM于E，设BC与y轴的交点为N，‎ ‎∵四边形OABC是平行四边形，‎ ‎∴OA∥BC，OA＝BC，‎ ‎∴∠AOM＝∠CNM，‎ ‎∵BD∥y轴，‎ ‎∴∠CBD＝∠CNM，‎ ‎∴∠AOM＝∠CBD，‎ ‎∵CD与x轴平行，BD与y轴平行，‎ ‎∴∠CDB＝90°，BE⊥AM，‎ ‎∴∠CDB＝∠AMO，‎ ‎∴△AOM≌△CBD（AAS），‎ ‎∴OM＝BD‎=‎‎2‎，‎ ‎∵S△ABD‎=‎1‎‎2‎BD⋅AE=‎2，BD‎=‎‎2‎，‎ ‎∴AE＝2‎2‎，‎ ‎∵∠ADB＝135°，‎ ‎∴∠ADE＝45°，‎ ‎∴△ADE是等腰直角三角形，‎ ‎∴DE＝AE＝2‎2‎，‎ ‎∴D的纵坐标为3‎2‎，‎ 设A（m，‎2‎），则D（m﹣2‎2‎，3‎2‎），‎ ‎∵反比例函数y‎=‎kx（x＞0）的图象经过A、D两点，‎ ‎∴k‎=‎‎2‎m＝（m﹣2‎2‎）×3‎2‎，‎ 解得m＝3‎2‎，‎ ‎∴k‎=‎‎2‎m＝6．‎ 故选：D．‎ ‎3．（2020•苏州）如图，平行四边形OABC的顶点A在x轴的正半轴上，点D（3，2）在对角线OB上，反比例函数y‎=‎kx（k＞0，x＞0）的图象经过C、D两点．已知平行四边形OABC的面积是‎15‎‎2‎，则点B的坐标为（　　）‎ A．（4，‎8‎‎3‎） B．（‎9‎‎2‎，3） C．（5，‎10‎‎3‎） D．（‎24‎‎5‎，‎16‎‎5‎）‎ ‎【答案】B ‎【解答】解：∵反比例函数y‎=‎kx（k＞0，x＞0）的图象经过点D（3，2），‎ ‎∴2‎=‎k‎3‎，‎ ‎∴k＝6，‎ ‎∴反比例函数y‎=‎‎6‎x，‎ ‎∵OB经过原点O，‎ ‎∴设OB的解析式为y＝mx，‎ ‎∵OB经过点D（3，2），‎ 则2＝3m，‎ ‎∴m‎=‎‎2‎‎3‎，‎ ‎∴OB的解析式为y‎=‎‎2‎‎3‎x，‎ ‎∵反比例函数y‎=‎‎6‎x经过点C，‎ ‎∴设C（a，‎6‎a），且a＞0，‎ ‎∵四边形OABC是平行四边形，‎ ‎∴BC∥OA，S平行四边形OABC＝2S△OBC，‎ ‎∴点B的纵坐标为‎6‎a，‎ ‎∵OB的解析式为y‎=‎‎2‎‎3‎x，‎ ‎∴B（‎9‎a，‎6‎a），‎ ‎∴BC‎=‎9‎a-‎a，‎ ‎∴S△OBC‎=‎1‎‎2‎×‎6‎a×‎（‎9‎a‎-‎a），‎ ‎∴2‎×‎1‎‎2‎×‎6‎a×‎（‎9‎a‎-‎a）‎=‎‎15‎‎2‎，‎ 解得：a＝2或a＝﹣2（舍去），‎ ‎∴B（‎9‎‎2‎，3），‎ 故选：B．‎ ‎4．（2020•无锡）反比例函数y‎=‎kx与一次函数y‎=‎8‎‎15‎x+‎‎16‎‎15‎的图象有一个交点B（‎1‎‎2‎，m），则k的值为（　　）‎ A．1 B．2 C．‎2‎‎3‎ D．‎‎4‎‎3‎ ‎【答案】C ‎【解答】解：∵一次函数y‎=‎8‎‎15‎x+‎‎16‎‎15‎的图象过点B（‎1‎‎2‎，m），‎ ‎∴m‎=‎8‎‎15‎×‎1‎‎2‎+‎16‎‎15‎=‎‎4‎‎3‎，‎ ‎∴点B（‎1‎‎2‎，‎4‎‎3‎），‎ ‎∵反比例函数y‎=‎kx过点B，‎ ‎∴k‎=‎1‎‎2‎×‎4‎‎3‎=‎‎2‎‎3‎，‎ 故选：C．‎ ‎5．（2019•徐州）若A（x1，y1）、B（x2，y2）都在函数y‎=‎‎2019‎x的图象上，且x1＜0＜x2，则（　　）‎ A．y1＜y2 B．y1＝y2 C．y1＞y2 D．y1＝﹣y2‎ ‎【答案】A ‎【解答】解：∵函数y‎=‎‎2019‎x，‎ ‎∴该函数图象在第一、三象限、在每个象限内y随x的增大而减小，‎ ‎∵A（x1，y1）、B（x2，y2）都在函数y‎=‎‎2019‎x的图象上，且x1＜0＜x2，‎ ‎∴y1＜y2，‎ 故选：A．‎ ‎6．（2019•淮安）当矩形面积一定时，下列图象中能表示它的长y和宽x之间函数关系的是（　　）‎ A． B． ‎ C． D．‎ ‎【答案】B ‎【解答】解：∵根据题意xy＝矩形面积（定值），‎ ‎∴y是x的反比例函数，（x＞0，y＞0）．‎ 故选：B．‎ ‎7．（2019•扬州）若反比例函数y‎=-‎‎2‎x的图象上有两个不同的点关于y轴的对称点都在一次函数y＝﹣x+m的图象上，则m的取值范围是（　　）‎ A．m＞2‎2‎ B．m＜﹣2‎2‎ ‎ C．m＞2‎2‎或m＜﹣2‎2‎ D．﹣2‎2‎‎＜‎m＜2‎‎2‎ ‎【答案】C ‎【解答】解：∵反比例函数y‎=-‎‎2‎x的图象上有两个不同的点关于y轴的对称点在反比例函数y‎=‎‎2‎x的图象上，‎ ‎∴解方程组y=‎‎2‎xy=-x+m得x2﹣mx+2＝0，‎ ‎∵y‎=‎‎2‎x的图象与一次函数y＝﹣x+m有两个不同的交点，‎ ‎∴方程x2﹣mx+2＝0有两个不同的实数根，‎ ‎∴△＝m2﹣8＞0，‎ ‎∴m＞2‎2‎或m＜﹣2‎2‎，‎ 故选：C．‎ ‎8．（2019•宿迁）如图，在平面直角坐标系xOy中，菱形ABCD的顶点A与原点O重合，顶点B落在x轴的正半轴上，对角线AC、BD交于点M，点D、M恰好都在反比例函数y‎=‎kx（x＞0）的图象上，则ACBD的值为（　　）‎ A．‎2‎ B．‎3‎ C．2 D．‎‎5‎ ‎【答案】A ‎【解答】解：设D（m，km），B（t，0），‎ ‎∵M点为菱形对角线的交点，‎ ‎∴BD⊥AC，AM＝CM，BM＝DM，‎ ‎∴M（m+t‎2‎，k‎2m），‎ 把M（m+t‎2‎，k‎2m）代入y‎=‎kx得m+t‎2‎•k‎2m‎=‎k，‎ ‎∴t＝3m，‎ ‎∵四边形ABCD为菱形，‎ ‎∴OD＝AB＝t，‎ ‎∴m2+（km）2＝（3m）2，解得k＝2‎2‎m2，‎ ‎∴M（2m，‎2‎m），‎ 在Rt△ABM中，tan∠MAB‎=BMAM=‎2‎m‎2m=‎‎1‎‎2‎，‎ ‎∴ACBD‎=‎‎2‎．‎ 故选：A．‎ ‎9．（2019•无锡）如图，已知A为反比例函数y‎=‎kx（x＜0）的图象上一点，过点A作AB⊥y轴，垂足为B．若△OAB的面积为2，则k的值为（　　）‎ A．2 B．﹣2 C．4 D．﹣4‎ ‎【答案】D ‎【解答】解：‎ ‎∵AB⊥y轴，‎ ‎∴S△OAB‎=‎‎1‎‎2‎|k|，‎ ‎∴‎1‎‎2‎|k|＝2，‎ ‎∵k＜0，‎ ‎∴k＝﹣4．‎ 故选：D．‎ ‎10．（2018•徐州）如图，在平面直角坐标系中，函数y＝kx与y‎=-‎‎2‎x的图象交于A，B两点，过A作y轴的垂线，交函数y‎=‎‎4‎x的图象于点C，连接BC，则△ABC的面积为（　　）‎ A．2 B．4 C．6 D．8‎ ‎【答案】C ‎【解答】解：∵正比例函数y＝kx与反比例函数y‎=-‎‎2‎x的图象交点关于原点对称，‎ ‎∴设A点坐标为（x，‎-‎‎2‎x），则B点坐标为（﹣x，‎2‎x），C（﹣2x，‎-‎‎2‎x），‎ ‎∴S△ABC‎=‎1‎‎2‎×‎（﹣2x﹣x）•（‎-‎2‎x-‎‎2‎x）‎=‎1‎‎2‎×‎（﹣3x）•（‎-‎‎4‎x）＝6．‎ 故选：C．‎ ‎11．（2018•镇江）如图，一次函数y＝2x与反比例函数y‎=‎kx（k＞0）的图象交于A，B两点，点P在以C（﹣2，0）为圆心，1为半径的⊙C上，Q是AP的中点，已知OQ长的最大值为‎3‎‎2‎，则k的值为（　　）‎ A．‎49‎‎32‎ B．‎25‎‎18‎ C．‎32‎‎25‎ D．‎‎9‎‎8‎ ‎【答案】C ‎【解答】解：连接BP，‎ 由对称性得：OA＝OB，‎ ‎∵Q是AP的中点，‎ ‎∴OQ‎=‎‎1‎‎2‎BP，‎ ‎∵OQ长的最大值为‎3‎‎2‎，‎ ‎∴BP长的最大值为‎3‎‎2‎‎×‎2＝3，‎ 如图，当BP过圆心C时，BP最长，过B作BD⊥x轴于D，‎ ‎∵CP＝1，‎ ‎∴BC＝2，‎ ‎∵B在直线y＝2x上，‎ 设B（t，2t），则CD＝t﹣（﹣2）＝t+2，BD＝﹣2t，‎ 在Rt△BCD中，由勾股定理得：BC2＝CD2+BD2，‎ ‎∴22＝（t+2）2+（﹣2t）2，‎ t＝0（舍）或‎-‎‎4‎‎5‎，‎ ‎∴B（‎-‎‎4‎‎5‎，‎-‎‎8‎‎5‎），‎ ‎∵点B在反比例函数y‎=‎kx（k＞0）的图象上，‎ ‎∴k‎=-‎4‎‎5‎×(-‎8‎‎5‎)=‎‎32‎‎25‎；‎ 故选：C．‎ ‎12．（2018•苏州）如图，矩形ABCD的顶点A，B在x轴的正半轴上，反比例函数y‎=‎kx在第一象限内的图象经过点D，交BC于点E．若AB＝4，CE＝2BE，tan∠AOD‎=‎‎3‎‎4‎，则k的值为（　　）‎ A．3 B．2‎3‎ C．6 D．12‎ ‎【答案】A ‎【解答】解：∵tan∠AOD‎=ADOA=‎‎3‎‎4‎，‎ ‎∴设AD＝3a、OA＝4a，‎ 则BC＝AD＝3a，点D坐标为（4a，3a），‎ ‎∵CE＝2BE，‎ ‎∴BE‎=‎‎1‎‎3‎BC＝a，‎ ‎∵AB＝4，‎ ‎∴点E（4+4a，a），‎ ‎∵反比例函数y‎=‎kx经过点D、E，‎ ‎∴k＝12a2＝（4+4a）a，‎ 解得：a‎=‎‎1‎‎2‎或a＝0（舍），‎ 则k＝12‎×‎1‎‎4‎=‎3，‎ 故选：A．‎ ‎13．（2018•淮安）若点A（﹣2，3）在反比例函数y‎=‎kx的图象上，则k的值是（　　）‎ A．﹣6 B．﹣2 C．2 D．6‎ ‎【答案】A ‎【解答】解：将A（﹣2，3）代入反比例函数y‎=‎kx，得 k＝﹣2×3＝﹣6，‎ 故选：A．‎ ‎14．（2018•无锡）已知点P（a，m），Q（b，n）都在反比例函数y‎=-‎‎2‎x的图象上，且a＜0＜b，则下列结论一定正确的是（　　）‎ A．m+n＜0 B．m+n＞0 C．m＜n D．m＞n ‎【答案】D ‎【解答】解：y‎=-‎‎2‎x的k＝﹣2＜0，图象位于二四象限，‎ ‎∵a＜0，‎ ‎∴P（a，m）在第二象限，‎ ‎∴m＞0；‎ ‎∵b＞0，‎ ‎∴Q（b，n）在第四象限，‎ ‎∴n＜0．‎ ‎∴n＜0＜m，‎ 即m＞n，‎ 故D正确；‎ 故选：D．‎ ‎15．（2018•连云港）如图，菱形ABCD的两个顶点B、D在反比例函数y‎=‎kx的图象上，对角线AC与BD 的交点恰好是坐标原点O，已知点A（1，1），∠ABC＝60°，则k的值是（　　）‎ A．﹣5 B．﹣4 C．﹣3 D．﹣2‎ ‎【答案】C ‎【解答】解：∵四边形ABCD是菱形，‎ ‎∴BA＝BC，AC⊥BD，‎ ‎∵∠ABC＝60°，‎ ‎∴△ABC是等边三角形，‎ ‎∵点A（1，1），‎ ‎∴OA‎=‎‎2‎，‎ ‎∴BO‎=OAtan30°‎=‎‎6‎，‎ ‎∵直线AC的解析式为y＝x，‎ ‎∴直线BD的解析式为y＝﹣x，‎ ‎∵OB‎=‎‎6‎，‎ ‎∴点B的坐标为（‎-‎‎3‎，‎3‎），‎ ‎∵点B在反比例函数y‎=‎kx的图象上，‎ ‎∴‎3‎‎=‎k‎-‎‎3‎，‎ 解得，k＝﹣3，‎ 故选：C．‎ ‎16．（2018•扬州）已知点A（x1，3），B（x2，6）都在反比例函数y‎=-‎‎3‎x的图象上，则下列关系式一定正确的是（　　）‎ A．x1＜x2＜0 B．x1＜0＜x2 C．x2＜x1＜0 D．x2＜0＜x1‎ ‎【答案】A ‎【解答】解：由题意，得 k＝﹣3，图象位于第二象限，或第四象限，‎ 在每一象限内，y随x的增大而增大，‎ ‎∵3＜6，‎ ‎∴x1＜x2＜0，‎ 故选：A．‎ 二．填空题（共10小题）‎ ‎17．（2020•宿迁）如图，点A在反比例函数y‎=‎kx（x＞0）的图象上，点B在x轴负半轴上，直线AB交y轴于点C，若ACBC‎=‎‎1‎‎2‎，△AOB的面积为6，则k的值为　6　．‎ ‎【答案】6．‎ ‎【解答】解：过点A作AD⊥y轴于D，则△ADC∽△BOC，‎ ‎∴DCOC‎=ACBC=‎‎1‎‎2‎，‎ ‎∵ACBC‎=‎‎1‎‎2‎，△AOB的面积为6，‎ ‎∴S‎△AOC‎=‎1‎‎3‎S‎△AOB=‎2，‎ ‎∴S‎△ACD‎=‎1‎‎2‎S‎△AOC=‎1，‎ ‎∴△AOD的面积＝3，‎ 根据反比例函数k的几何意义得，‎1‎‎2‎‎|k|=3‎，‎ ‎∴|k|＝6，‎ ‎∵k＞0，‎ ‎∴k＝6．‎ 故答案为：6．‎ ‎18．（2020•南通）将双曲线y‎=‎‎3‎x向右平移1个单位长度，再向下平移2个单位长度，得到的新双曲线与直线y＝kx﹣2﹣k（k＞0）相交于两点，其中一个点的横坐标为a，另一个点的纵坐标为b，则（a﹣1）（b+2）＝　﹣3　．‎ ‎【答案】﹣3．‎ ‎【解答】解：一次函数y＝kx﹣2﹣k（k＞0）的图象过定点P（1，﹣2），而点P（1，﹣2）恰好是原点（0，0）向右平移1个单位长度，再向下平移2个单位长度得到的，‎ 因此将双曲线y‎=‎‎3‎x向右平移1个单位长度，再向下平移2个单位长度，得到的新双曲线与直线y＝kx﹣2﹣k（k＞0）相交于两点，在没平移前是关于原点对称的，‎ 平移前，这两个点的坐标为（a﹣1，‎3‎a-1‎），（‎3‎b+2‎，b+2），‎ ‎∴a﹣1‎=-‎‎3‎b+2‎，‎ ‎∴（a﹣1）（b+2）＝﹣3．‎ 故答案为：﹣3．‎ ‎19．（2020•淮安）如图，等腰△ABC的两个顶点A（﹣1，﹣4）、B（﹣4，﹣1）在反比例函数y‎=‎k‎1‎x（x＜0）的图象上，AC＝BC．过点C作边AB的垂线交反比例函数y‎=‎k‎1‎x（x＜0）的图象于点D，动点P从点D出发，沿射线CD方向运动3‎2‎个单位长度，到达反比例函数y‎=‎k‎2‎x（x＞0）图象上一点，则k2＝　1　．‎ ‎【答案】见试题解答内容 ‎【解答】解：把A（﹣1，﹣4）代入y‎=‎k‎1‎x中得，k1＝4，‎ ‎∴反比例函数y‎=‎k‎1‎x为y=‎‎4‎x，‎ ‎∵A（﹣1，﹣4）、B（﹣4，﹣1），‎ ‎∴AB的垂直平分线为y＝x，‎ 联立方程驵y=‎‎4‎xy=x，解得x=-2‎y=-2‎，或x=2‎y=2‎，‎ ‎∵AC＝BC，CD⊥AB，‎ ‎∴CD是AB的垂直平分线，‎ ‎∵CD与反比例函数y‎=‎k‎1‎x（x＜0）的图象于点D，‎ ‎∴D（﹣2，﹣2），‎ ‎∵动点P从点D出发，沿射线CD方向运动3‎2‎个单位长度，到达反比例函数y‎=‎k‎2‎x（x＞0）图象上一点，‎ ‎∴设移动后的点P的坐标为（m，m）（m＞﹣2），则 ‎(m+2‎)‎‎2‎+(m+2‎‎)‎‎2‎‎=‎‎3‎2‎，‎ ‎∴m＝1，‎ ‎∴P（1，1），‎ 把P（1，1）代入y‎=‎k‎2‎x（x＞0）中，得k2＝1，‎ 故答案为：1．‎ ‎20．（2020•盐城）如图，已知点A（5，2）、B（5，4）、C（8，1）．直线l⊥x轴，垂足为点M（m，0）．其中m‎＜‎‎5‎‎2‎，若△A′B′C′与△ABC关于直线l对称，且△A′B′C′有两个顶点在函数y‎=‎kx（k≠0）的图象上，则k的值为　﹣6或﹣4　．‎ ‎【答案】见试题解答内容 ‎【解答】解：∵点A（5，2）、B（5，4）、C（8，1），直线l⊥x轴，垂足为点M（m，0）．其中m‎＜‎‎5‎‎2‎，△A′B′C′与△ABC关于直线l对称，‎ ‎∴A′（2m﹣5，2），B′（2m﹣5，4），C′（2m﹣8，1），‎ ‎∵A′、B′的横坐标相同，‎ ‎∴在函数y‎=‎kx（k≠0）的图象上的两点为，A′、C′或B′、C′，‎ 当A′、C′在函数y‎=‎kx（k≠0）的图象上时，则k＝2（2m﹣5）＝2m﹣8，解得m＝1，‎ ‎∴k＝﹣6；‎ 当B′、C′在函数y‎=‎kx（k≠0）的图象上时，则k＝4（2m﹣5）＝2m﹣8，解得m＝2，‎ ‎∴k＝﹣4，‎ 综上，k的值为﹣6或﹣4，‎ 故答案为﹣6或﹣4．‎ ‎21．（2020•泰州）如图，点P在反比例函数y‎=‎‎3‎x的图象上，且横坐标为1，过点P作两条坐标轴的平行线，与反比例函数y‎=‎kx（k＜0）的图象相交于点A、B，则直线AB与x轴所夹锐角的正切值为　3　．‎ ‎【答案】见试题解答内容 ‎【解答】解：点P在反比例函数y‎=‎‎3‎x的图象上，且横坐标为1，则点P（1，3），‎ 则点A、B的坐标分别为（1，k），（‎1‎‎3‎k，3），‎ 设直线AB的表达式为：y＝mx+t，将点A、B的坐标代入上式得k=m+t‎3=‎1‎‎3‎km+t，解得m＝﹣3，‎ 故直线AB与x轴所夹锐角的正切值为3，‎ 故答案为3．‎ ‎22．（2019•无锡）如图，A为反比例函数y‎=‎kx（k＜0）的图象上一点，AP⊥y轴，垂足为P．点B在直线AP上，且PB＝3PA，过点B作直线BC∥y轴，交反比例函数的图象于点C，若△PAC的面积为4，则k的值为　﹣6或﹣12　．‎ ‎【答案】见试题解答内容 ‎【解答】解：当B点在P点右侧，如图，‎ 设A（t，kt），‎ ‎∵PB＝3PA，‎ ‎∴B（﹣3t，kt），‎ ‎∵BC∥y轴，‎ ‎∴C（﹣3t，‎-‎k‎3t），‎ ‎∵△PAC的面积为4，‎ ‎∴‎1‎‎2‎‎×‎（﹣t）×（kt‎+‎k‎3t）＝4，解得k＝﹣6；‎ 当B点在P点左侧，‎ 设A（t，kt），‎ ‎∵PB＝3PA，‎ ‎∴B（3t，kt），‎ ‎∵BC∥y轴，‎ ‎∴C（3t，k‎3t），‎ ‎∵△PAC的面积为4，‎ ‎∴‎1‎‎2‎‎×‎（﹣t）×（kt‎-‎k‎3t）＝4，解得k＝﹣12；‎ 综上所述，k的值为﹣6或﹣12．‎ 故答案为﹣6或﹣12．‎ ‎23．（2019•南通）如图，过点C（3，4）的直线y＝2x+b交x轴于点A，∠ABC＝90°，AB＝CB，曲线y‎=‎kx ‎（x＞0）过点B，将点A沿y轴正方向平移a个单位长度恰好落在该曲线上，则a的值为　4　．‎ ‎【答案】见试题解答内容 ‎【解答】解：作CD⊥x轴于D，BF⊥x轴于F，过B作BE⊥CD于E，‎ ‎∵过点C（3，4）的直线y＝2x+b交x轴于点A，‎ ‎∴4＝2×3+b，解得b＝﹣2，‎ ‎∴直线为y＝2x﹣2，‎ 令y＝0，则求得x＝1，‎ ‎∴A（1，0），‎ ‎∵BF⊥x轴于F，过B作BE⊥CD于E，‎ ‎∴BE∥x轴，‎ ‎∴∠ABE＝∠BAF，‎ ‎∵∠ABC＝90°，‎ ‎∴∠ABE+∠EBC＝90°，‎ ‎∵∠BAF+∠ABF＝90°，‎ ‎∴∠EBC＝∠ABF，‎ 在△EBC和△FBA中 ‎∠EBC=∠ABF‎∠BEC=∠BFA=90°‎BC=AB‎ ‎ ‎∴△EBC≌△FBA（AAS），‎ ‎∴CE＝AF，BE＝BF，‎ 设B（m，km），‎ ‎∵4‎-km=‎m﹣1，m﹣3‎=‎km，‎ ‎∴4﹣（m﹣3）＝m﹣1，‎ 解得m＝4，k＝4，‎ ‎∴反比例函数的解析式为y‎=‎‎4‎x，‎ 把x＝1代入得y＝4，‎ ‎∴a＝4﹣0＝4，‎ ‎∴a的值为4．‎ 故答案为4．‎ ‎24．（2019•镇江）已知点A（﹣2，y1）、B（﹣1，y2）都在反比例函数y‎=-‎‎2‎x的图象上，则y1　＜　y2．（填“＞”或“＜”）‎ ‎【答案】见试题解答内容 ‎【解答】解：∵反比例函数y‎=-‎‎2‎x的图象在二、四象限，而A（﹣2，y1）、B（﹣1，y2）都在第二象限，‎ ‎∴在第二象限内，y随x的增大而增大，‎ ‎∵﹣2＜﹣1‎ ‎∴y1＜y2．‎ 故答案为：＜‎ ‎25．（2019•无锡）某个函数具有性质：当x＞0时，y随x的增大而增大，这个函数的表达式可以是　y＝x2（答案不唯一）　（只要写出一个符合题意的答案即可）．‎ ‎【答案】见试题解答内容 ‎【解答】解：y＝x2中开口向上，对称轴为x＝0，‎ 当x＞0时y随着x的增大而增大，‎ 故答案为：y＝x2（答案不唯一）．‎ ‎26．（2018•无锡）已知点A、B都在反比例函数y‎=‎‎6‎x（x＞0）的图象上，其横坐标分别是m、n（m＜n）．过点A分别向x轴、y轴作垂线，垂足分别是C、D；过点B分别向x轴、y轴作垂线，垂足分别是E、F，AC与BF交于点P．当点P在线段DE上、且m（n﹣2）＝3时，m的值等于　‎1+‎‎7‎‎2‎　．‎ ‎【答案】见试题解答内容 ‎【解答】解：如图，A（m，‎6‎m），B（n，‎6‎n），则P（m，‎6‎n），‎ ‎∵点P在线段DE上，AD∥CE，‎ ‎∴△ADP∽△CEP，‎ ‎∴ADCE‎=‎APPC，即mn-m‎=‎‎6‎m‎-‎‎6‎n‎6‎n，‎ ‎∴m2＝（n﹣m）2，‎ 而n＞m＞0，‎ ‎∴m＝n﹣m，即n＝2m，‎ 把n＝2m代入m（n﹣2）＝2得m（2m﹣2）＝3，‎ 整理得2m2﹣2m﹣3＝0，解得m1‎=‎‎1+‎‎7‎‎2‎，m2‎=‎‎1-‎‎7‎‎2‎（舍去），‎ 即m的值为‎1+‎‎7‎‎2‎．‎ 故答案为‎1+‎‎7‎‎2‎．‎ 三．解答题（共16小题）‎ ‎27．（2020•镇江）如图，正比例函数y＝kx（k≠0）的图象与反比例函数y‎=-‎‎8‎x的图象交于点A（n，2）和点B．‎ ‎（1）n＝　﹣4　，k＝　‎-‎‎1‎‎2‎　；‎ ‎（2）点C在y轴正半轴上．∠ACB＝90°，求点C的坐标；‎ ‎（3）点P（m，0）在x轴上，∠APB为锐角，直接写出m的取值范围．‎ ‎【答案】（1）﹣4；‎-‎‎1‎‎2‎；‎ ‎（2）C（0，2‎5‎）；‎ ‎（3）m＜﹣2‎5‎或m＞2‎5‎．‎ ‎【解答】解：（1）把A（n，2）代入反比例函数y‎=-‎‎8‎x中，得n＝﹣4，‎ ‎∴A（﹣4，2），‎ 把A（﹣4，2）代入正比例函数y＝kx（k≠0）中，得k‎=-‎‎1‎‎2‎，‎ 故答案为：﹣4；‎-‎‎1‎‎2‎；‎ ‎（2）过A作AD⊥y轴于D，过B作BE⊥y轴于E，‎ ‎∵A（﹣4，2），‎ ‎∴根据双曲线与正比例函数图象的对称性得B（4，﹣2），‎ 设C（0，b），则CD＝b﹣2，AD＝4，BE＝4，CE＝b+2，‎ ‎∵∠ACO+∠OCB＝90°，∠OCB+∠CBE＝90°，‎ ‎∴∠ACO＝∠CBE，‎ ‎∵∠ADC＝∠CEB＝90°，‎ ‎∴△ACD∽△CBE，‎ ‎∴CDBE‎=‎ADCE，即b-2‎‎4‎‎=‎‎4‎b+2‎，‎ 解得，b＝2‎5‎，或b＝﹣2‎5‎（舍），‎ ‎∴C（0，2‎5‎）；‎ 另一解法：∵A（﹣4，2），‎ ‎∴根据双曲线与正比例函数图象的对称性得B（4，﹣2），‎ ‎∴AB=‎64+16‎=4‎‎5‎，‎ ‎∵∠ACB＝90°，OA＝OB，‎ ‎∴OC=‎1‎‎2‎AB=2‎‎5‎，‎ ‎∴C(0，2‎‎5‎）；‎ ‎（3）如图2，过A作AM⊥x轴于M，过B作BN⊥x轴于N，在x轴上原点的两旁取两点P1，P2，使得OP1＝OP2＝OA＝OB，‎ ‎∴OP‎1‎=OP‎2‎=OA=‎4‎‎2‎‎+‎‎2‎‎2‎=2‎‎5‎，‎ ‎∴P1（﹣2‎5‎，0），P2（2‎5‎，0），‎ ‎∵OP1＝OP2＝OA＝OB，‎ ‎∴四边形AP1BP2为矩形，‎ ‎∴AP1⊥P1B，AP2⊥BP2，‎ ‎∵点P（m，0）在x轴上，∠APB为锐角，‎ ‎∴P点必在P1的左边或P2的右边，‎ ‎∴m＜﹣2‎5‎或m＞2‎5‎．‎ 另一解法：在x轴上原点的两旁取两点P1，P2，使得∠AP1B＝∠AP2B＝90°，‎ 则OP‎1‎=OP‎2‎=‎1‎‎2‎AB=2‎‎5‎，‎ ‎∴P‎1‎‎(-2‎5‎，0)，P‎2‎(2‎5‎，0)‎，‎ ‎∵点P（m，0）在x轴上，∠APB为锐角，‎ ‎∴P点必在P1的左边或P2的右边，‎ ‎∴m＜﹣2‎5‎或m＞2‎5‎．‎ ‎28．（2020•常州）如图，正比例函数y＝kx的图象与反比例函数y‎=‎‎8‎x（x＞0）的图象交于点A（a，4）．点B为x轴正半轴上一点，过B作x轴的垂线交反比例函数的图象于点C，交正比例函数的图象于点D．‎ ‎（1）求a的值及正比例函数y＝kx的表达式；‎ ‎（2）若BD＝10，求△ACD的面积．‎ ‎【答案】（1）a＝2，y＝2x；‎ ‎（2）12.6．‎ ‎【解答】解：（1）把点A（a，4）代入反比例函数y‎=‎‎8‎x（x＞0）得，‎ a‎=‎8‎‎4‎=‎2，‎ ‎∴点A（2，4），代入y＝kx得，k＝2，‎ ‎∴正比例函数的关系式为y＝2x；‎ ‎（2）当BD＝10＝y时，代入y＝2x得，x＝5，‎ ‎∴OB＝5，‎ 当x＝5代入y‎=‎‎8‎x得，y‎=‎‎8‎‎5‎，即BC‎=‎‎8‎‎5‎，‎ ‎∴CD＝BD﹣BC＝10‎-‎8‎‎5‎=‎‎42‎‎5‎，‎ ‎∴S△ACD‎=‎1‎‎2‎×‎42‎‎5‎×‎（5﹣2）＝12.6，‎ ‎29．（2020•徐州）如图，在平面直角坐标系中，一次函数y＝kx+b的图象经过点A（0，﹣4）、B（2，0‎ ‎），交反比例函数y‎=‎mx（x＞0）的图象于点C（3，a），点P在反比例函数的图象上，横坐标为n（0＜n＜3），PQ∥y轴交直线AB于点Q，D是y轴上任意一点，连接PD、QD．‎ ‎（1）求一次函数和反比例函数的表达式；‎ ‎（2）求△DPQ面积的最大值．‎ ‎【答案】见试题解答内容 ‎【解答】解：（1）把A（0，﹣4）、B（2，0）代入一次函数y＝kx+b得，‎ b=-4‎‎2k+b=0‎‎，解得，k=2‎b=-4‎，‎ ‎∴一次函数的关系式为y＝2x﹣4，‎ 当x＝3时，y＝2×3﹣4＝2，‎ ‎∴点C（3，2），‎ ‎∵点C在反比例函数的图象上，‎ ‎∴k＝3×2＝6，‎ ‎∴反比例函数的关系式为y‎=‎‎6‎x，‎ 答：一次函数的关系式为y＝2x﹣4，反比例函数的关系式为y‎=‎‎6‎x；‎ ‎（2）点P在反比例函数的图象上，点Q在一次函数的图象上，‎ ‎∴点P（n，‎6‎n），点Q（n，2n﹣4），‎ ‎∴PQ‎=‎6‎n-‎（2n﹣4），‎ ‎∴S△PDQ‎=‎‎1‎‎2‎n[‎6‎n‎-‎（2n﹣4）]＝﹣n2+2n+3＝﹣（n﹣1）2+4，‎ ‎∵﹣1＜0，‎ ‎∴当n＝1时，S最大＝4，‎ 答：△DPQ面积的最大值是4．‎ ‎30．（2020•扬州）如图，已知点A（1，2）、B（5，n）（n＞0），点P为线段AB上的一个动点，反比例函数y‎=‎kx（x＞0）的图象经过点P．小明说：“点P从点A运动至点B的过程中，k值逐渐增大，当点P在点A位置时k值最小，在点B位置时k值最大．”‎ ‎（1）当n＝1时．‎ ‎①求线段AB所在直线的函数表达式．‎ ‎②你完全同意小明的说法吗？若完全同意，请说明理由；若不完全同意，也请说明理由，并求出正确的k的最小值和最大值．‎ ‎（2）若小明的说法完全正确，求n的取值范围．‎ ‎【答案】见试题解答内容 ‎【解答】解：（1）①当n＝1时，B（5，1），‎ 设线段AB所在直线的函数表达式为y＝mx+n，‎ 把A（1，2）和B（5，1）代入得：m+n=2‎‎5m+n=1‎，‎ 解得：m=-‎‎1‎‎4‎n=‎‎9‎‎4‎，‎ 则线段AB所在直线的函数表达式为y‎=-‎‎1‎‎4‎x‎+‎‎9‎‎4‎；‎ ‎②不完全同意小明的说法，理由为：‎ k＝xy＝x（‎-‎‎1‎‎4‎x‎+‎‎9‎‎4‎）‎=-‎‎1‎‎4‎（x‎-‎‎9‎‎2‎）2‎+‎‎81‎‎16‎，‎ ‎∵1≤x≤5，‎ ‎∴当x＝1时，kmin＝2；‎ 当x‎=‎‎9‎‎2‎时，kmax‎=‎‎81‎‎16‎，‎ 则不完全同意；‎ ‎（2）当n＝2时，A（1，2），B（5，2），符合；‎ 当n≠2时，y‎=‎n-2‎‎4‎x‎+‎‎10-n‎4‎，‎ k＝x（n-2‎‎4‎x‎+‎‎10-n‎4‎）‎=‎n-2‎‎4‎（x‎-‎n-10‎‎2n-4‎）2‎+‎‎(10-n‎)‎‎2‎‎16(2-n)‎，‎ 当n＜2时，k随x的增大而增大，则有n-10‎‎2n-4‎‎≥‎5，‎ 此时‎10‎‎9‎‎≤‎n＜2；‎ 当n＞2时，k随x的增大而增大，则有n-10‎‎2n-4‎‎≤‎1，‎ 此时n＞2，‎ 综上，n‎≥‎‎10‎‎9‎．‎ ‎31．（2020•南京）已知反比例函数y‎=‎kx的图象经过点（﹣2，﹣1）．‎ ‎（1）求k的值．‎ ‎（2）完成下面的解答．‎ 解不等式组‎2-x＞1，①‎kx‎＞1．②‎ 解：解不等式①，得　x＜1　．‎ 根据函数y‎=‎kx的图象，得不等式②的解集　0＜x＜2　．‎ 把不等式①和②的解集在数轴上表示出来．‎ 从图中可以找出两个不等式解集的公共部分，得不等式组的解集　0＜x＜1　．‎ ‎【答案】见试题解答内容 ‎【解答】解：（1）∵反比例函数y‎=‎kx的图象经过点（﹣2，﹣1），‎ ‎∴k＝（﹣2）×（﹣1）＝2；‎ ‎（2）解不等式组‎2-x＞1，①‎kx‎＞1．②‎ 解：解不等式①，得x＜1．‎ 根据函数y‎=‎kx的图象，得不等式②的解集0＜x＜2．‎ 把不等式①和②的解集在数轴上表示为：‎ ‎∴不等式组的解集为0＜x＜1，‎ 故答案为：x＜1，0＜x＜2，0＜x＜1．‎ ‎32．（2020•连云港）如图，在平面直角坐标系xOy中，反比例函数y‎=‎mx（x＞0）的图象经过点A（4，‎3‎‎2‎），点B在y轴的负半轴上，AB交x轴于点C，C为线段AB的中点．‎ ‎（1）m＝　6　，点C的坐标为　（2，0）　；‎ ‎（2）若点D为线段AB上的一个动点，过点D作DE∥y轴，交反比例函数图象于点E，求△ODE面积的最大值．‎ ‎【答案】见试题解答内容 ‎【解答】解：（1）∵反比例函数y‎=‎mx（x＞0）的图象经过点A（4，‎3‎‎2‎），‎ ‎∴m‎=4×‎3‎‎2‎=‎6，‎ ‎∵AB交x轴于点C，C为线段AB的中点．‎ ‎∴C（2，0）；‎ 故答案为6，（2，0）；‎ ‎（2）设直线AB的解析式为y＝kx+b，‎ 把A（4，‎3‎‎2‎），C（2，0）代入得‎4k+b=‎‎3‎‎2‎‎2k+b=0‎，解得k=‎‎3‎‎4‎b=-‎‎3‎‎2‎，‎ ‎∴直线AB的解析式为y‎=‎‎3‎‎4‎x‎-‎‎3‎‎2‎；‎ ‎∵点D为线段AB上的一个动点，‎ ‎∴设D（x，‎3‎‎4‎x‎-‎‎3‎‎2‎）（0＜x≤4），‎ ‎∵DE∥y轴，‎ ‎∴E（x，‎6‎x），‎ ‎∴S△ODE‎=‎‎1‎‎2‎x•（‎6‎x‎-‎‎3‎‎4‎x‎+‎‎3‎‎2‎）‎=-‎‎3‎‎8‎x2‎+‎‎3‎‎4‎x+3‎=-‎‎3‎‎8‎（x﹣1）2‎+‎‎27‎‎8‎，‎ ‎∴当x＝1时，△ODE的面积的最大值为‎27‎‎8‎．‎ ‎33．（2019•无锡）如图，一次函数y＝x+3的图象与反比例函数y‎=‎kx（x＞0）的图象相交于点A（1，m），与x轴相交于点B．‎ ‎（1）求这个反比例函数的表达式；‎ ‎（2）C为反比例函数的图象上异于点A的一点，直线AC交x轴于点D，设直线AC所对应的函数表达式为y＝nx+b．‎ ‎①若△ABD的面积为12，求n、b的值；‎ ‎②作CE⊥x轴，垂足为E，记t＝OE•DE，求n•t的值．‎ ‎【答案】见试题解答内容 ‎【解答】解：（1）把x＝1代入y＝x+3，得y＝4，‎ ‎∴m＝4，‎ ‎∴A点坐标为：（1，4），‎ ‎∴k＝4，‎ 则反比例函数表达式为：y‎=‎‎4‎x；‎ ‎（2）①∵△ABD的面积为12，A（1，4），‎ ‎∴BD＝6，‎ 把y＝0代入y＝x+3，得x＝﹣3，‎ ‎∴B点坐标为：（﹣3，0），‎ ‎∴D点的坐标为：（3，0），‎ 把x＝1，y＝4；x＝3，y＝0，分别代入y＝nx+b，‎ n+b=4‎‎3n+b=0‎‎ ‎ 解得：n=-2‎b=6‎，‎ ‎②把x＝1，y＝4代入得：n+b＝4，得b＝4﹣n，‎ 令y＝0，得x‎=‎n-4‎n，‎ ‎∴点D的坐标为：（n-4‎n，0），‎ 当‎4‎x‎=‎nx+4﹣n时，‎ 解得：x1＝1，x2‎=-‎‎4‎n，‎ ‎∴点E的坐标为：（‎-‎‎4‎n，0），‎ ‎∴OE‎=-‎‎4‎n，‎ ‎∴DE‎=n-4‎n-‎（‎-‎‎4‎n）＝1，‎ ‎∵t＝OE•DE‎=-‎‎4‎n，‎ ‎∴n•t＝﹣4．‎ ‎34．（2019•徐州）如图，平面直角坐标系中，O为原点，点A、B分别在y轴、x轴的正半轴上．△AOB的两条外角平分线交于点P，P在反比例函数y‎=‎‎9‎x的图象上．PA的延长线交x轴于点C，PB的延长线交y轴于点D，连接CD．‎ ‎（1）求∠P的度数及点P的坐标；‎ ‎（2）求△OCD的面积；‎ ‎（3）△AOB的面积是否存在最大值？若存在，求出最大面积；若不存在，请说明理由．‎ ‎【答案】见试题解答内容 ‎【解答】解：（1）如图，作PM⊥OA于M，PN⊥OB于N，PH⊥AB于H．‎ ‎∴∠PMA＝∠PHA＝90°，‎ ‎∵∠PAM＝∠PAH，PA＝PA，‎ ‎∴△PAM≌△PAH（AAS），‎ ‎∴PM＝PH，∠APM＝∠APH，‎ 同理可证：△BPN≌△BPH，‎ ‎∴PH＝PN，∠BPN＝∠BPH，‎ ‎∴PM＝PN，‎ ‎∵∠PMO＝∠MON＝∠PNO＝90°，‎ ‎∴四边形PMON是矩形，‎ ‎∴∠MPN＝90°，‎ ‎∴∠APB＝∠APH+∠BPH‎=‎‎1‎‎2‎（∠MPH+∠NPH）＝45°，‎ ‎∵PM＝PN，‎ ‎∴可以假设P（m，m），‎ ‎∵P（m，m）在y‎=‎‎9‎x上，‎ ‎∴m2＝9，‎ ‎∵m＞0，‎ ‎∴m＝3，‎ ‎∴P（3，3）．‎ ‎（2）设OA＝a，OB＝b，则AM＝AH＝3﹣a，BN＝BH＝3﹣b，‎ ‎∴AB＝6﹣a﹣b，‎ ‎∵AB2＝OA2+OB2，‎ ‎∴a2+b2＝（6﹣a﹣b）2，‎ 可得ab＝6a+6b﹣18，‎ ‎∴3a+3b﹣9‎=‎‎1‎‎2‎ab，‎ ‎∵PM∥OC，‎ ‎∴COPM‎=‎OAAM，‎ ‎∴OC‎3‎‎=‎a‎3-a，‎ ‎∴OC‎=‎‎3a‎3-a，同法可得OD‎=‎‎3b‎3-b，‎ ‎∴S△COD‎=‎‎1‎‎2‎•OC•DO‎=‎‎1‎‎2‎•‎9ab‎(3-a)(3-b)‎‎=‎‎1‎‎2‎•‎9ab‎9-3a-3b+ab‎=‎‎1‎‎2‎•‎9ab‎-‎1‎‎2‎ab+ab‎=‎9．‎ 解法二：证明△COP∽△POD，得OC•OD＝OP2＝18，可求△COD的面积等于9．‎ ‎（3）设OA＝a，OB＝b，则AM＝AH＝3﹣a，BN＝BH＝3﹣b，‎ ‎∴AB＝6﹣a﹣b，‎ ‎∴OA+OB+AB＝6，‎ ‎∴a+b‎+a‎2‎‎+‎b‎2‎=‎6，‎ ‎∴2ab‎+‎2ab≤‎6，‎ ‎∴（2‎+‎‎2‎）ab‎≤‎6，‎ ‎∴ab‎≤‎3（2‎-‎‎2‎），‎ ‎∴ab≤54﹣36‎2‎，‎ ‎∴S△AOB‎=‎‎1‎‎2‎ab≤27﹣18‎2‎，‎ ‎∴△AOB的面积的最大值为27﹣18‎2‎．‎ ‎35．（2019•镇江）如图，点A（2，n）和点D是反比例函数y‎=‎mx（m＞0，x＞0）图象上的两点，一次函数y＝kx+3（k≠0）的图象经过点A，与y轴交于点B，与x轴交于点C，过点D作DE⊥x轴，垂足为E，连接OA，OD．已知△OAB与△ODE的面积满足S△OAB：S△ODE＝3：4．‎ ‎（1）S△OAB＝　3　，m＝　8　；‎ ‎（2）已知点P（6，0）在线段OE上，当∠PDE＝∠CBO时，求点D的坐标．‎ ‎【答案】见试题解答内容 ‎【解答】解：（1）由一次函数y＝kx+3知，B（0，3）．‎ 又点A的坐标是（2，n），‎ ‎∴S△OAB‎=‎1‎‎2‎×‎3×2＝3．‎ ‎∵S△OAB：S△ODE＝3：4．‎ ‎∴S△ODE＝4．‎ ‎∵点D是反比例函数y‎=‎mx（m＞0，x＞0）图象上的点，‎ ‎∴‎1‎‎2‎m＝S△ODE＝4，则m＝8．‎ 故答案是：3；8；‎ ‎（2）由（1）知，反比例函数解析式是y‎=‎‎8‎x．‎ ‎∴2n＝8，即n＝4．‎ 故A（2，4），将其代入y＝kx+3得到：2k+3＝4．‎ 解得k‎=‎‎1‎‎2‎．‎ ‎∴直线AC的解析式是：y‎=‎‎1‎‎2‎x+3．‎ 令y＝0，则‎1‎‎2‎x+3＝0，‎ ‎∴x＝﹣6，‎ ‎∴C（﹣6，0）．‎ ‎∴OC＝6．‎ 由（1）知，OB＝3．‎ 设D（a，b），则DE＝b，PE＝a﹣6．‎ ‎∵∠PDE＝∠CBO，∠COB＝∠PED＝90°，‎ ‎∴△CBO∽△PDE，‎ ‎∴OBDE‎=‎OCPE，即‎3‎b‎=‎‎6‎a-6‎①，‎ 又ab＝8 ②．‎ 联立①②，得a=-2‎b=-4‎（舍去）或a=8‎b=1‎．‎ 故D（8，1）．‎ ‎36．（2019•常州）如图，在▱OABC中，OA＝2‎2‎，∠AOC＝45°，点C在y轴上，点D是BC的中点，反比例函数y‎=‎kx（x＞0）的图象经过点A、D．‎ ‎（1）求k的值；‎ ‎（2）求点D的坐标．‎ ‎【答案】见试题解答内容 ‎【解答】解：（1）∵OA＝2‎2‎，∠AOC＝45°，‎ ‎∴A（2，2），‎ ‎∴k＝4，‎ ‎∴y‎=‎‎4‎x．‎ ‎（2）四边形OABC是平行四边形OABC，‎ ‎∴AB⊥x轴，‎ ‎∴B的横坐标为2，‎ ‎∵点D是BC的中点，‎ ‎∴D点的横坐标为1，‎ ‎∴D（1，4）．‎ ‎37．（2019•苏州）如图，A为反比例函数y‎=‎kx（其中x＞0）图象上的一点，在x轴正半轴上有一点B，OB＝4．连接OA，AB，且OA＝AB＝2‎10‎．‎ ‎（1）求k的值；‎ ‎（2）过点B作BC⊥OB，交反比例函数y‎=‎kx（其中x＞0）的图象于点C，连接OC交AB于点D，求ADDB的值．‎ ‎【答案】见试题解答内容 ‎【解答】解：（1）过点A作AH⊥x轴，垂足为点H，AH交OC于点M，如图所示．‎ ‎∵OA＝AB，AH⊥OB，‎ ‎∴OH＝BH‎=‎‎1‎‎2‎OB＝2，‎ ‎∴AH‎=OA‎2‎-OH‎2‎=‎6，‎ ‎∴点A的坐标为（2，6）．‎ ‎∵A为反比例函数y‎=‎kx图象上的一点，‎ ‎∴k＝2×6＝12．‎ ‎（2）∵BC⊥x轴，OB＝4，点C在反比例函数y‎=‎‎12‎x上，‎ ‎∴BC‎=kOB=‎3．‎ ‎∵AH∥BC，OH＝BH，‎ ‎∴MH‎=‎‎1‎‎2‎BC‎=‎‎3‎‎2‎，‎ ‎∴AM＝AH﹣MH‎=‎‎9‎‎2‎．‎ ‎∵AM∥BC，‎ ‎∴△ADM∽△BDC，‎ ‎∴ADDB‎=AMBC=‎‎3‎‎2‎．‎ ‎38．（2019•宿迁）如图，一次函数y＝kx+b的图象与反比例函数y‎=-‎‎5‎x的图象相交于点A（﹣1，m）、B（n，﹣1）两点．‎ ‎（1）求一次函数表达式；‎ ‎（2）求△AOB的面积．‎ ‎【答案】见试题解答内容 ‎【解答】解：（1）把A（﹣1．m），B（n，﹣1）代入y‎=-‎‎5‎x，得m＝5，n＝5，‎ ‎∴A（﹣1，5），B（5，﹣1），‎ 把A（﹣1，5），B（5，﹣1）代入y＝kx+b得 ‎-k+b=5‎‎5k+b=-1‎‎，解得k=-1‎b=4‎，‎ ‎∴一次函数解析式为y＝﹣x+4；‎ ‎（2）x＝0时，y＝4，‎ ‎∴OD＝4，‎ ‎∴△AOB的面积＝S△AOD+S△BOD‎=‎1‎‎2‎×‎4×1‎+‎1‎‎2‎×4×5=‎12．‎ ‎39．（2019•泰州）已知一次函数y1＝kx+n（n＜0）和反比例函数y2‎=‎mx（m＞0，x＞0）．‎ ‎（1）如图1，若n＝﹣2，且函数y1、y2的图象都经过点A（3，4）．‎ ‎①求m，k的值；‎ ‎②直接写出当y1＞y2时x的范围；‎ ‎（2）如图2，过点P（1，0）作y轴的平行线l与函数y2的图象相交于点B，与反比例函数y3‎=‎nx（x＞0）的图象相交于点C．‎ ‎①若k＝2，直线l与函数y1的图象相交点D．当点B、C、D中的一点到另外两点的距离相等时，求m﹣n的值；‎ ‎②过点B作x轴的平行线与函数y1的图象相交于点E．当m﹣n的值取不大于1的任意实数时，点B、C间的距离与点B、E间的距离之和d始终是一个定值．求此时k的值及定值d．‎ ‎【答案】见试题解答内容 ‎【解答】解：（1）①将点A的坐标代入一次函数表达式并解得：k＝2，‎ 将点A的坐标代入反比例函数得：m＝3×4＝12；‎ ‎②由图象可以看出x＞3时，y1＞y2；‎ ‎（2）①当x＝1时，点D、B、C的坐标分别为（1，2+n）、（1，m）、（1，n），‎ 则BD＝|2+n﹣m|，BC＝m﹣n，DC＝2+n﹣n＝2‎ 则BD＝BC或BD＝DC或BC＝CD，‎ 即：|2+n﹣m|＝m﹣n或|2+n﹣m|＝2或m﹣n＝2，‎ 即：m﹣n＝1或0或2或4，‎ 当m﹣n＝0时，m＝n与题意不符，‎ 点D不能在C的下方，即BC＝CD也不存在，n+2＞n，‎ 当B、D重合时，m﹣n＝2成立，‎ 故m﹣n＝1或4或2；‎ ‎②点E的横坐标为：m-nk，‎ 当点E在点B左侧时，‎ d＝BC+BE＝m﹣n+（1‎-‎m-nk）＝1+（m﹣n）（1‎-‎‎1‎k），‎ m﹣n的值取不大于1的任意数时，d始终是一个定值，‎ 当1‎-‎1‎k=‎0时，此时k＝1，从而d＝1．‎ 当点E在点B右侧时，‎ 同理BC+BE＝（m﹣n）（1‎+‎‎1‎k）﹣1，‎ 当1‎+‎1‎k=‎0，k＝﹣1时，（不合题意舍去）‎ 故k＝1，d＝1．‎ ‎40．（2019•连云港）如图，在平面直角坐标系xOy中，函数y＝﹣x+b的图象与函数y‎=‎kx（x＜0）的图象相交于点A（﹣1，6），并与x轴交于点C．点D是线段AC上一点，△ODC与△OAC的面积比为2：3．‎ ‎（1）k＝　﹣6　，b＝　5　；‎ ‎（2）求点D的坐标；‎ ‎（3）若将△ODC绕点O逆时针旋转，得到△OD'C'，其中点D'落在x轴负半轴上，判断点C'是否落在函数y‎=‎kx（x＜0）的图象上，并说明理由．‎ ‎【答案】见试题解答内容 ‎【解答】解：（1）将A（﹣1，6）代入y＝﹣x+b，‎ 得，6＝1+b，‎ ‎∴b＝5，‎ 将A（﹣1，6）代入y‎=‎kx，‎ 得，6‎=‎k‎-1‎，‎ ‎∴k＝﹣6，‎ 故答案为：﹣6，5；‎ ‎（2）如图1，过点D作DM⊥x轴，垂足为M，过点A作AN⊥x轴，垂足为N，‎ ‎∵S‎△ODCS‎△OAC‎=‎1‎‎2‎OC⋅DM‎1‎‎2‎OC⋅AN=‎‎2‎‎3‎，‎ ‎∴DMAN‎=‎‎2‎‎3‎，‎ 又∵点A的坐标为（﹣1，6），‎ ‎∴AN＝6，‎ ‎∴DM＝4，即点D的纵坐标为4，‎ 把y＝4代入y＝﹣x+5中，‎ 得，x＝1，‎ ‎∴D（1，4）；‎ ‎（3）由题意可知，OD'＝OD‎=OM‎2‎+DM‎2‎=‎‎17‎，‎ 如图2，过点C'作C'G⊥x轴，垂足为G，‎ ‎∵S△ODC＝S△OD'C'，‎ ‎∴OC•DM＝OD'•C'G，‎ 即5×4‎=‎‎17‎C'G，‎ ‎∴C'G‎=‎‎20‎‎17‎‎17‎，‎ 在Rt△OC'G中，‎ ‎∵OG‎=OC'‎‎2‎‎-C'‎G‎2‎=‎25-‎‎400‎‎17‎=‎‎5‎‎17‎‎17‎，‎ ‎∴C'的坐标为（‎-‎‎5‎‎17‎‎17‎，‎20‎‎17‎‎17‎），‎ ‎∵（‎-‎‎5‎‎17‎‎17‎）‎×‎20‎‎17‎‎17‎≠-‎6，‎ ‎∴点C'不在函数y‎=-‎‎6‎x的图象上．‎ ‎41．（2019•盐城）如图，一次函数y＝x+1的图象交y轴于点A，与反比例函数y‎=‎kx（x＞0）的图象交于点B（m，2）．‎ ‎（1）求反比例函数的表达式；‎ ‎（2）求△AOB的面积．‎ ‎【答案】见试题解答内容 ‎【解答】解：（1）∵点B（m，2）在直线y＝x+1上，‎ ‎∴2＝m+1，得m＝1，‎ ‎∴点B的坐标为（1，2），‎ ‎∵点B（1，2）在反比例函数y‎=‎kx（x＞0）的图象上，‎ ‎∴2‎=‎k‎1‎，得k＝2，‎ 即反比例函数的表达式是y‎=‎‎2‎x；‎ ‎（2）将x＝0代入y＝x+1，得y＝1，‎ 则点A的坐标为（0，1），‎ ‎∵点B的坐标为（1，2），‎ ‎∴△AOB的面积是；‎1×1‎‎2‎‎=‎‎1‎‎2‎．‎ ‎42．（2019•泰安）已知一次函数y＝kx+b的图象与反比例函数y‎=‎mx的图象交于点A，与x轴交于点B（5，0），若OB＝AB，且S△OAB‎=‎‎15‎‎2‎．‎ ‎（1）求反比例函数与一次函数的表达式；‎ ‎（2）若点P为x轴上一点，△ABP是等腰三角形，求点P的坐标．‎ ‎【答案】见试题解答内容 ‎【解答】解：（1）如图1，过点A作AD⊥x轴于D，‎ ‎∵B（5，0），‎ ‎∴OB＝5，‎ ‎∵S△OAB‎=‎‎15‎‎2‎，‎ ‎∴‎1‎‎2‎‎×‎5×AD‎=‎‎15‎‎2‎，‎ ‎∴AD＝3，‎ ‎∵OB＝AB，‎ ‎∴AB＝5，‎ 在Rt△ADB中，BD‎=AB‎2‎-AD‎2‎=‎4，‎ ‎∴OD＝OB+BD＝9，‎ ‎∴A（9，3），‎ 将点A坐标代入反比例函数y‎=‎mx中得，m＝9×3＝27，‎ ‎∴反比例函数的解析式为y‎=‎‎27‎x，‎ 将点A（9，3），B（5，0）代入直线y＝kx+b中，‎9k+b=3‎‎5k+b=0‎，‎ ‎∴k=‎‎3‎‎4‎b=-‎‎15‎‎4‎，‎ ‎∴直线AB的解析式为y‎=‎‎3‎‎4‎x‎-‎‎15‎‎4‎；‎ ‎（2）由（1）知，AB＝5，‎ ‎∵△ABP是等腰三角形，‎ ‎∴①当AB＝PB时，‎ ‎∴PB＝5，‎ ‎∴P（0，0）或（10，0），‎ ‎②当AB＝AP时，如图2，‎ 由（1）知，BD＝4，‎ 易知，点P与点B关于AD对称，‎ ‎∴DP＝BD＝4，‎ ‎∴OP＝5+4+4＝13，∴P（13，0），‎ ‎③当PB＝AP时，设P（a，0），‎ ‎∵A（9，3），B（5，0），‎ ‎∴AP2＝（9﹣a）2+9，BP2＝（5﹣a）2，‎ ‎∴（9﹣a）2+9＝（5﹣a）2‎ ‎∴a‎=‎‎65‎‎8‎，‎ ‎∴P（‎65‎‎8‎，0），‎ 即：满足条件的点P的坐标为（0，0）或（10，0）或（13，0）或（‎65‎‎8‎，0）．‎